Les variables
Les variables
Définition
Un algorithme est une suite d’opérations pour obtenir un résultat.
Exemple
On souhaite à l’aide d’un algorithme calculer n’importe quelle image de la fonction :
$f(x) = -2(x + 3)$.
Au début, il s’agit de déclarer trois variables, qui sont des cases de mémoire dans lesquelles il est possible de stocker des nombres.
- Variables : $x, a, b$
On demande ensuite à l’utilisateur de saisir le nombre pour lequel il souhaite calculer son image.
- Entrée : Saisir $x$.
On écrit ensuite la liste des opérations dans laquelle on indique par une flèche ($\to$) que l’on stocke le nombre à gauche dans la variable de droite.
- Traitement :
$-2x \to a$
$x + 3 \to b$
On souhaite ensuite calculer $a \times b$.
Pour stocker le résultat, il est possible d’introduire une nouvelle variable mais il est également possible de stocker le résultat dans une variable déjà existante si l’on ne souhaite plus se servir de la valeur qu’elle contenait.
$a \times b \to a$
Enfin, on affiche le résultat.
- Sortie :
Afficher $a$.
En résumé, l’algorithme sera :
- Variables :
$x, a, b$
- Entrée :
Saisir $x$.
- Traitement :
$-2x \to a$
$x + 3 \to b$
$a \times b \to a$
- Sortie :
Afficher $a$.
On peut résumer les valeurs prises par les variables dans un tableau:
| $x$ | $a$ | $b$ |
| 3 | -6 | 6 |
| -36 |
Le test
Le test
Les algorithmes permettent d’effectuer des tests (regarder la parité d’un nombre par exemple).
Il existe des tests sous la forme : SI…. ALORS…
On peut aussi utiliser des tests du type : SI…. ALORS… SINON…
Exemple :
On choisit un entier $n$.
Si il est pair, on le divise par 2.
Si il est impair, alors on le multiplie par 3 et on ajoute 1 au résultat.
On traduit cet énoncé sous forme d’algorithme :
- Variables : $n, a$
- Entrée : Saisir $n$ (On choisit un nombre entier que l’on stocke dans la variable $n$)
- Traitement : (on effectue le test)
Si $n$ est pair
Alors $\dfrac{n}{2} \to a$
Sinon $3n + 1 \to a$
Fin du Si
- Sortie : Afficher $a$
Il s’agit d’une boucle et il n’est pas nécessaire d’avoir l’instruction Sinon mais il faut prêter attention à bien écrire la fin de la boucle (Fin du Si).
Il est possible d’améliorer cet algorithme en utilisant uniquement la variable $n$ mais il est plus difficile de se relire.
La boucle Pour
La boucle Pour
Dans un algorithme, il est possible de vouloir écrire une boucle que l’on souhaite répéter un nombre de fois connu : on utilise alors une boucle Pour.
Exemple :
On souhaite lancer $n$ fois un dé à six faces et afficher à chaque fois la face obtenue.
Un algorithme qui traduit cet exemple est le suivant.
Variables : $n, f$ (où $n$ est le nombre de répétitions de la boucle, c’est à dire le nombre de lancés et $f$ la face obtenue lors d’un lancé)
Entrée : Saisir $n$ (on indique le nombre de fois que l’on souhaite lancer le dé)
Traitement : (on écrit la boucle Pour, on utilise un nombre $i$ appelé compteur qui varie de 1 à 6 et qui compte ainsi le nombre de répétitions des opérations comprises entre les instructions Pour et Fin Pour)
Pour $i$ allant de 1 à $n$
nombre_entier(1, 6) $\to f$ (il s’agit d’une fonctionnalité préexistante qui permet de donner un nombre entier compris entre 1 et 6 aléatoirement)
Afficher $f$
Fin Pour
Sortie
Sans les commentaires, l’algorithme est donc :
- Variables : $n, f$
- Entrée : Saisir $n$
- Traitement : Pour $i$ allant de 1 à $n$
nombre_entier(1, 6) $\to f$
Afficher $f$
Fin Pour
- Sortie
Remarque :
On considère par exemple que l’on souhaite faire $n = 3$ lancés.
Au début $i$ vaut 1. La fonction nombre_entier(1, 6) donne la face obtenue puis on l’affiche.
On recommence ensuite la boucle, $i$ vaut alors 2. A nouveau, la fonction nombre_entier(1, 6) donne la face obtenue puis on l’affiche.
On recommence de même la boucle, $i$ vaut alors 3. On obtient un nombre au hasard que l’on affiche.
Enfin, $i$ valant 3, on quitte la boucle et le programme se termine.
Si on avait écrit l’instruction “Afficher $f$” en dehors de la boucle, l’algorithme aurait alors stocké 6 fois une face et aurait à la fin de la boucle affiché la dernière face obtenue.
La boucle Tant que
La boucle Tant que
Lors de certains algorithmes, il est possible d’utiliser des boucles dont on ignore le nombre de répétitions : ce sont les boucles Tant que.
Exemple :
on dispose d’une population d’individus de 3000 habitants qui augmente chaque année de 2%.
On se demande au bout de combien d’années la population aura dépassé 4000 habitants mais on ignore le nombre d’années : on utilise donc une boucle Tant que.
On écrit donc un algorithme qui permettra de trouver le nombre d’années $N$ pour que la population $P$ dépasse 4000.
- Variables : $N, P$
- Entrée : $3000 \to P$
$0 \to N$
- Traitement : (on traduit la question avec un boucle)
Tant que $P < 4000$ (on souhaite connaitre l’année où la population dépasse 4000 habitants donc tant qu’elle est inférieure à 4000 on continue les calculs et on arrête la première fois qu’elle dépasse 4000).
$ P + 0,02P \to P$
$N + 1 \to N$
Fin Tant que
- Sortie : Afficher $N$
Sans les commentaires, l’algorithme est :
Variables : $N, P$
Entrée : $3000 \to P$
$0 \to N$
Traitement : Tant que $P < 4000$
$P + 0,02P \to P$
$N + 1 \to N$
Fin Tant que
Sortie : Afficher $N$
On peut regarder les différentes valeurs que prennent $N$ et $P$ au début et à la fin de l’algorithme.
Ainsi, au bout d’un an, la population atteint 3060 habitants, $P = 3060$ et $N=1$.
Or $P < 4000$, on continue donc les calculs.
Au bout de 14 années, la population vaut environ $P \approx 3958$.
Mais un an plus tard, au bout de 15 ans, la population vaut $P \approx 4037 > 4000$.
On ne rentre donc plus dans la boucle Tant que et on affiche la valeur de $N$ c’est à dire 15.
Ainsi, il aura fallu 15 ans pour que la population dépasse 4000 habitants.
Le tableau d’avancement du programme est le suivant :
| $P$ | $N$ |
| 3000 | 0 |
| 3060 | 1 |
| $\vdots$ | $\vdots$ |
| $\approx 3958$ | 14 |
| $\approx 4037$ | 15 |
Les suites (série S)
Les suites (algorithmes)
On considère la suite $(U_n)$ définie pour tout $n \in \mathbb{N}$ par $\left \{ \begin{array}{l} U_{n+1} = 2 U_n + 5 \\ U_0 = 1 \end{array} \right.$.
Cette suite n’est ni arithmétique, ni géométrique : on ne dispose d’aucune formule pour calculer directement le $n^{\text{ème}}$ terme de la suite ni pour calculer sa somme.
Exemple
On cherche le rang $N$ de la suite tel que $U_n > 50$.
Variables : $N, U$
Entrée :
$ 0 \to N$, $N$ est le compteur du rang$
$1 \to U$ $U$ est le terme $U_N$
Traitement :
Tant que $U \leq 50$
$2U + 5 \to U$
$N + 1 \to N$
Fin du Tant que
Sortie : Afficher $N$
Lorsque l’on rentre pour la première fois dans la boucle, $U$ vaut 1.
On calcule alors $U_1 = 7 \leq 50$, on continue donc le calcul du terme suivant et ainsi de suite.
L’algorithme s’arrête $N = 11$ : ainsi $U_{11} > 50$.
Autre exemple
On souhaite à présent calculer $S_4 = U_0 + U_1 + U_2 + U_3 + U_4$.
Variables : $N, U, S$
Entrée:
Saisir $N$ (on demande à l’utilisateur de rentrer jusqu’à quel terme de la suite il souhaite calculer la somme, ici $N = 4$)
$1 \to U$
$U \to S$, on stocke $U$ dans $S$ car $S_0 = U_0$.
Traitement :
Pour $i$ allant de 1 à $N =4$ (on utilise la boucle pour car on connait le nombre d’itérations)
$2U + 5 \to U$
$U + S \to S$
Fin du Pour
Sortie : Afficher $S$
Dichotomie
Dichotomie
L’algorithme de dichotomie est une succession d’opérations permettant de donner un encadrement de la solution de l’équation $f(x) = 0$.
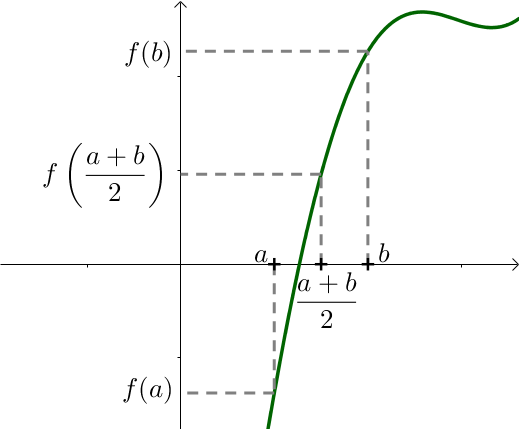
On cherche à savoir pour quelles valeurs une fonction $f$ s’annule, en raisonnant en tâtonnant. On choisit de manière arbitraire deux nombres $a$ et $b$ tels que $f(a) < 0$ et $f(b) > 0$.
La fonction est d’abord négative puis positive : elle passe donc par 0.
On se place ensuite au milieu de l’intervalle, c’est à dire $\dfrac{a + b}{2}$ puis on calcule l’image par la fonction $f$ de ce nouveau point que l’on compare à 0.
Ici, $f\left ( \dfrac{a + b}{2} \right ) > 0$.
On en déduit alors que la fonction s’annule dans l’intervalle $\left [a; \dfrac{a + b}{2} \right ]$.
On prend donc pour nouvelle valeur de $b$ la valeur du milieu $\dfrac{a + b}{2}$ et on conserve la même valeur pour $a$.
Puis on recommence le même procédé : on considère le milieu de l’intervalle puis on calcule l’image par la fonction $f$ de ce nouveau point.
Ici, l’image est négative, on se place donc sur la deuxième moitié de l’intervalle : le nombre $a$ change cette fois ci pour devenir $\dfrac{a + b}{2}$.
On réitère ce procédé autant de fois qu’on le souhaite pour approcher la solution à la précision désirée.
On peut alors réaliser un tableau résumant les différentes étapes de calcul de cet algorithme comprenant les valeurs de $a, b, \dfrac{a + b}{2}$ et le signe de leur image par la fonction $f$.
| Etape | 1 | 2 |
| $a$ | 1 | 1 |
| $b$ | 2 | 1,5 |
| $\dfrac{a + b}{2}$ | 1,5 | 1,25 |
| $f(a)$ | $-$ | $-$ |
| $f(b)$ | $+$ | $+$ |
| $f\left ( \dfrac{a + b}{2} \right )$ | $+$ | $-$ |
On se propose de commenter l’algorithme ci-dessous.
On indique dans un premier temps les variables utilisées dans l’algorithme.
L’entrée correspond aux valeurs que l’utilisateur doit rentrer.
$N$ correspond au nombre d’itérations de l’algorithme, c’est à dire le nombre de fois où l’on va chercher le milieu de l’intervalle et calculer son image par la fonction $f$ et étudier son signe.
Le traitement correspond à l’algorithme. $k$ compte le nombre d’itérations en cours, $m$ correspond au milieu de l’intervalle d’étude.
Enfin, on affiche les bornes de l’intervalle final qui donne un encadrement de la solution $f(x) = 0$.