Calculs de limites de fonctions trigonométriques
Ce cours du chapitre Fonctions sinus et cosinus traite des calculs de limites de fonctions trigonométriques. Il aborde plus précisément les limites au voisinage de l’infini (méthode du théorème des gendarmes) et la limite en $0$ (en faisant apparaître un taux de variation).
Calculs de limites de fonctions trigonométriques : ce que tu vas réviser
Comment calculer la limite d’une fonction trigonométrique ?
Il existe plusieurs types de limites de fonctions trigonométriques et donc plusieurs façons de les calculer : limites au voisinage de l’infini grâce au théorème des gendarmes et limites en 0 grâce au taux de variation.
I – Limites au voisinage de l’infini
Comment déterminer la limite d’une fonction avec sinus ?
Les fonctions cosinus et sinus n’ont pas de limite en $+\infty$ ni en $-\infty$.
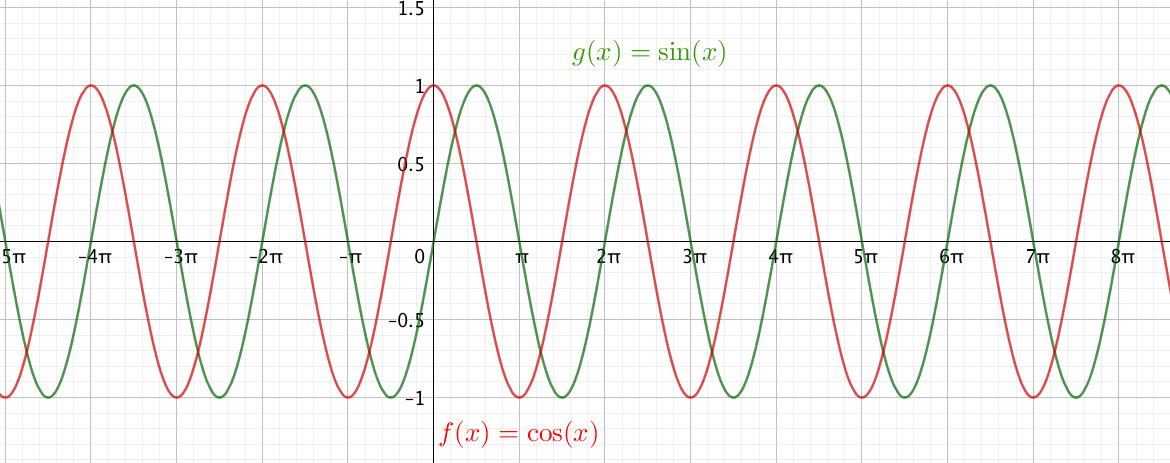
Cependant, on peut comparer leurs croissances aux puissances de $x$ :
$\displaystyle \lim_{x\to \pm \infty} \dfrac{\cos(x)}{x^n}=0$ avec $n\in \mathbb{N}^\star$
$\displaystyle \lim_{x\to \pm \infty} \dfrac{\sin(x)}{x^n}=0$ avec $n\in\mathbb{N}^\star$
Ces résultats s’obtiennent très facilement avec le théorème des gendarmes.
Théorème des gendarmes :
Si deux fonctions $f$ et $h$ admettent la même limite en un point $a$, et qu’une troisième fonction $g$ se trouve prise en étau entre $f$ et $h$ dans le voisinage de $a$, alors $g$ admet en $a$ une limite qui est égale à la limite commune de $f$ et $h$.
II – Limite en $0$
En faisant apparaître un taux de variation, on montre que :
${\displaystyle\lim_{x\to 0}\dfrac{\sin(x)}{x}=1}$
Preuve :
$\displaystyle\lim_{x\to 0} \dfrac{\sin(x)}{x}=\lim_{x\to 0}\dfrac{\sin(x)-\sin(0)}{x-0} =\sin'(0) = \cos(0) = 1$
Exemple
Calculer la limite en $0$ de la fonction $f(x)=\dfrac{\sin(4x)}{x}$.
Il s’agit ici de faire apparaître un taux de variation pour pouvoir calculer cette limite qui est une forme indéterminée du type : $\dfrac00$.
Pour cela, on écrit $f(x) = 4 \times \dfrac{\sin(4x)}{4x}$.
Or, on sait que $\displaystyle\lim_{x\to 0}\dfrac{\sin(x)}{x}=1$ et si le nombre $x$ tend vers $0$ alors $4x$ tend aussi vers $0$.
Ainsi : $\displaystyle \lim_{x\to 0}\dfrac{\sin(4x)}{4x}=1$.
En multipliant par la constante $4$, on en déduit finalement la limite de $f$ en $0$ :
${\displaystyle\lim_{x\to 0}f(x)=4}$
Pour aller plus loin dans les Fonctions sinus et cosinus
Après avoir étudié ce cours, nous te conseillons de poursuivre avec ces autres notions :
Calculs de limites de fonctions trigonométriques - Exercice 1
Calculer des limites avec des théorèmes de comparaison
1) \(\lim\limits_{x \to +\infty} \frac{cos x}{x}\)
\(-1 \leq cos x \leq 1\)
\(\frac{-1}{x} \leq \frac{cos x}{x} \leq \frac{1}{x}\)
\(\lim\limits_{x \to +\infty} \frac{-1}{x} = 0\)
\(\lim\limits_{x \to +\infty} \frac{1}{x} = 0\)
\(\lim\limits_{x \to +\infty} \frac{cos x}{x} = 0\)
2) \(\lim\limits_{x \to -\infty} x + cos x\)
\(-1 \leq cos x \leq 1\)
\(-1+x \leq cos x + x \leq 1 + x\)
\(\lim\limits_{x \to -\infty} 1+x = -\infty\)
Donc \(\lim\limits_{x \to -\infty} cos x+x = -\infty\)
Calculs de limites de fonctions trigonométriques - Exercice 2
Calculer une limite avec un taux de variation
Rappel :
Si une fonction \(g\) est dérivable en \(a\), alors \( \lim\limits_{x \to a} \frac{g(x)-g(a)}{x-a} = g'(a)\)
Question :
Calculer \(\lim\limits_{x \to 0} \frac{cos\ x-1}{x}\)


