Calculs d'intégrales
Calculs d’intégrales
Propriété
Soit $f$ une fonction continue sur un intervalle $I$.
Soit $F$, une primitive de \(f\) sur $I$.
Pour tous réels $a$ et $b$ de l’intervalle $I$, on a :
$\displaystyle\int_{a}^b f(t) dt= F(b)- F(a) $ que l’on note aussi
$\displaystyle\int_{a}^b f(t) dt=\left[F(t)\right]_{a}^b$
Exemples
Calculer :
$I$=\(\displaystyle\int_{1}^2 \dfrac{x^2+3x+1}{x^2}dx\).
$J$=\(\displaystyle \int_{0}^1 x(2x^2-1)^3 dx\).
Correction
Calcul de $I$
Étape 1 : La fonction $f(x)= \dfrac{x^2+3x+1}{x^2}$ est définie et continue sur $[1;2]$.
On décompose l’expression en trois fractions de dénominateur commun.
$I$=\(\displaystyle\int_{1}^2 (\dfrac{x^2}{x^2}+\dfrac{3x}{x^2}+\dfrac{1}{x^2})dx\)
$I$=\(\displaystyle\int_{1}^2 (1+\dfrac{3}{x}+\dfrac{1}{x^2})dx\)
$I$=\(\displaystyle\int_{1}^2 dx+ \int_{1}^2\dfrac{3}{x}dx+ \int_{1}^2\dfrac{1}{x^2}dx\)
Étape 2 : On peut définir des primitives de chaque expression.
$I$= \(\displaystyle \left[x+3\ln x-\dfrac{1}{x}\right]_{1}^2\)
Étape 3 : On calcule $F(2)-F(1)$.
$I$= \(\displaystyle (2+3\ln 2-\dfrac{1}{2})-(1+3\ln 1-\dfrac{1}{1})\)
$I$= \(\displaystyle \dfrac{3}{2}+3\ln 2 \) (unité d’aire).
Calcul de $J$
On pose : $u(x)=2x^2-1$ et $u'(x)=4x$.
On modifie l’expression pour la faire apparaître sous la forme $u’\times u^3$.
$J$=\(\displaystyle \dfrac{1}{4} \int_{0}^1 4x(2x^2-1)^3 dx \)
$J$=\(\displaystyle \dfrac{1}{4}\left[\dfrac{1}{4}(2x^2-1)^4\right]_{0}^1 \)
$J$=\(\displaystyle \dfrac{1}{4}\left((\dfrac{1}{4}(1)^4)-(\dfrac{1}{4}(-1)^4)\right)\)
$J$=\(\displaystyle \dfrac{1}{4}\left(\dfrac{1}{4}-\dfrac{1}{4}\right)\)
$J$= $0$
Théorème des valeurs intermédiaires
Théorème des valeurs intermédiaires
Théorème
Soient $f$ une fonction continue sur un intervalle $I$ et $a$ et $b$ deux réels dans l’intervalle $I$ tels que $a\leqslant b $.
Alors, pour tout réel $k$ compris entre $f(a)$ et $f(b)$, il existe au moins un réel $c$ compris entre $a$ et $b$ tel que $f(c)=k$.
Illustration graphique
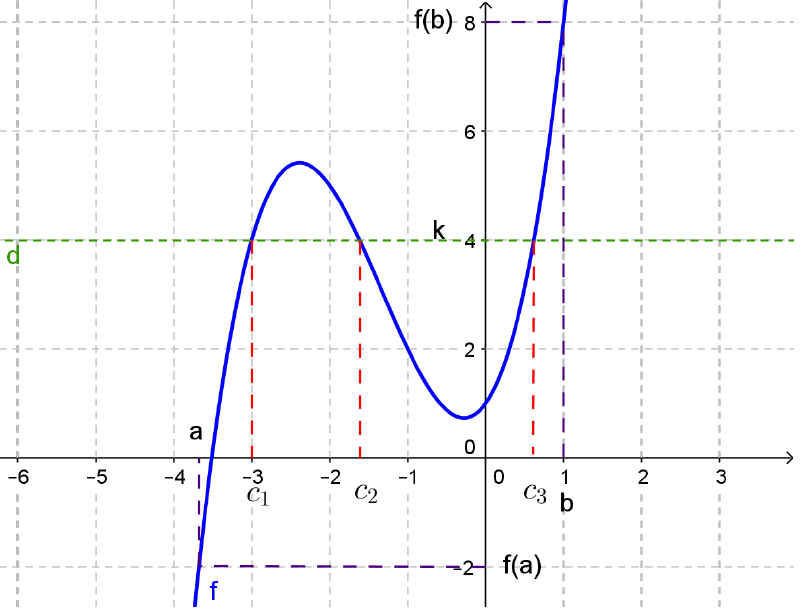
La fonction représentée en bleu est continue sur $I=[a,b]$.
Pour $k$ compris entre $f(a)$ et $f(b)$, on remarque graphiquement qu’il existe un $c_1$ dans $[a,b]$ tel que $f(c_1)=k$.
On voit, aussi qu’il existe deux autres $c_2$ et $c_3$ dans $[a,b]$ tels que $f(c_2)=k$ et $f(c_3)=k$. (D’où, dans le théorème, l’importance de l’expression “au moins”)
Cas des fonctions strictement monotones
Soit $f$ une fonction continue et strictement monotone sur un intervalle $[a,b]$ avec $a\leqslant b$.
Pour tout réel $k$ compris entre $f(a)$ et $f(b)$, il existe un unique réel $c$ compris entre $a$ et $b$ tel que $f(c)=k$.
Illustration graphique
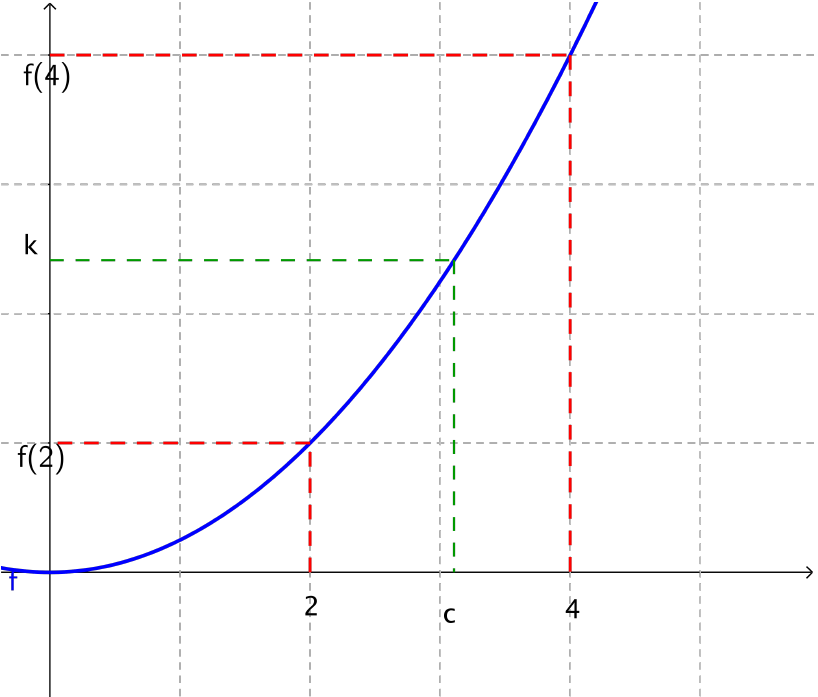
La fonction représentée en bleu est continue et strictement croissante sur $I=[2,4]$.
Pour $k$ compris entre $f(2)$ et $f(4)$, on remarque graphiquement qu’il existe un unique $c$ dans $[2,4]$ tel que $f(c)=k$.
Étude de la convexité d'une fonction
Étude de la convexité d’une fonction
Il existe deux principaux théorèmes permettant d’étudier l’éventuelle convexité ou concavité d’une fonction.
Théorème 1 :
Soit $f$ une fonction dérivable sur $I$,
1) $f$ est convexe sur $ I \ \iff \ f’$ est croissante sur $I$
2) $f$ est concave sur $ I \ \iff \ f’$ est décroissante sur $I$
Pour étudier la convexité d’une fonction, il suffit d’étudier les variations de sa dérivée.
Exemple :
Etudions la fonction $f(x) = x^2 -3x +2$ sur l’intervalle $I = \mathbb{R}$.
$f$ est une fonction polynôme, elle est donc dérivable sur $\mathbb{R}$ et $\ f'(x) = 2x – 3$.
La dérivée de $\ f$ est une fonction affine. Le cours permet de conclure que $\ f’$ est croissante car $2>0$.
Ainsi, comme $\ f’$ est croissante sur $I$, $f$ est convexe sur $I$.
Théorème 2 :
Soit $f$ une fonction dérivable sur $I$ et on suppose de plus que $\ f”$ existe sur $I$ ($f”$ est la dérivée de la dérivée : c’est la dérivée seconde de $f$),
1) si pour tout $x \in I, \ f”(x) \geq 0$, alors $\ f$ est convexe sur $I$
2) si pour tout $x \in I, \ f”(x) \leq 0$, alors $\ f$ est concave sur $I$
Ces deux théorèmes sont liés.
En effet, si on suppose que $\ f”(x) \geq 0$, cela implique que $\ f’$ est croissante et dans les deux cas, $f$ est convexe.
Exemple :
Soit $f(x) = x^2$, on veut démontrer que $f$ est convexe sur $\mathbb{R}$.
Soit $x \in \mathbb{R}$, on calcule dans un premier temps $\ f'(x) = 2x$ puis la dérivée seconde $\ f”(x) = 2 \geq 0$.
Ainsi, pour tout $x \in \mathbb{R}, \ f”(x) \geq 0$, donc $f$ est convexe sur $\mathbb{R}$.