Fonctions du second degré s’annulant en deux nombres réels distincts
Polynômes s'annulant en 2 nombres réels distincts
Polynôme s’annulant en deux nombres réels distincts
Factorisation d’un polynôme de discriminant positif
Soit $P$ un polynôme du second degré défini sur $\mathbb{R}$ par $P(x) = ax^2 + bx + c$ avec $a, \, b, \, c$ trois réels ($a \neq 0$).
On suppose que le discriminant est strictement positif, ($\Delta > 0)$.
Le polynôme admet donc deux racines $x_1$ et $x_2$ telles que $P(x_1) = 0$ et $P(x_2) = 0$.
Le polynôme $P$ se factorise donc sous la forme $P(x) = a (x – x_1) (x – x_2)$.
Exemple 1 : deux racines évidentes
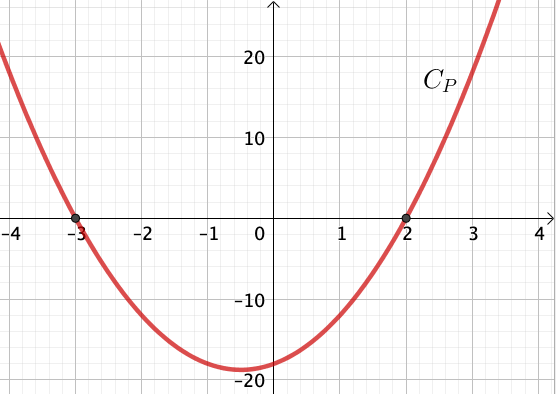
On suppose que $P(x) = 3x^2 + 3x – 18$.
Il n’est pas toujours nécessaire de calculer le discriminant.
On peut tester avec la calculatrice certaines valeurs évidentes de $x$ comme $-3; -2; -1; 0; 1; 2; 3;…$.
On trouve que $P(-3) = 0$ et $P(2) = 0$.
Ainsi $P(x) = 3 (x – 2) (x – (-3)) = 3(x – 2)(x + 3)$.
Graphiquement, les racines sont les abscisses des points d’intersection de la courbe avec l’axe des abscisses.
Comme $a = 3 > 0$, la parabole est dirigée “vers le haut”.
Exemple 2 : une seule racine évidente
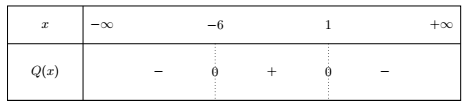
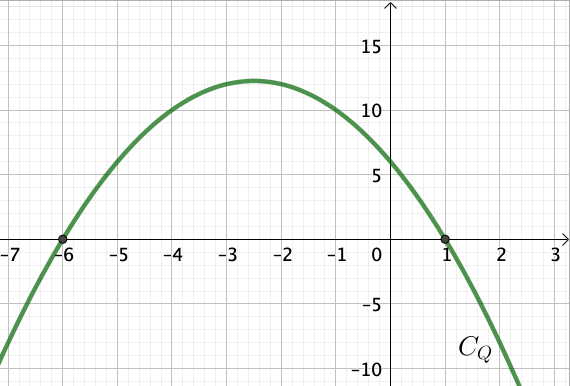
Soit $x \in \mathbb{R}$, on pose $Q(x) = -x^2 – 5x + 6$.
Comme la somme des coefficients vaut $0$ ($-1 – 5 + 6 = 0$), une racine évidente est $1$.
Pour trouver la seconde, on peut utiliser le fait que $x_1x_2 = \dfrac{c}{a} = \dfrac{6}{-1} = -6$ donc $x_2 = -6$.
Ou encore, on sait que $Q(x) = (x – 1)(a’x + b’)$ et en développant on trouve la valeur des coefficients $a’$ et $b’$ en les identifiant avec la forme initiale de $Q$.
Ainsi, $Q(x) = -(x – 1)(x + 6)$.
Comme $a = -1 < 0$, la courbe est dirigée “vers le bas”.
Exemple 3 : pas de racine évidente
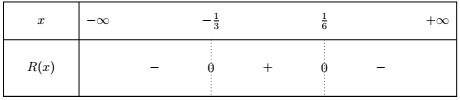
On suppose enfin que $R(x) = -3x^2 – \dfrac{1}{2} x + \dfrac{1}{6}$. On ne trouve pas de racine évidente dans ce cas.
En effectuant la méthode du discriminant, on trouve que $\Delta = \dfrac{9}{4} > 0$ et ainsi,
$x_1 = \dfrac{-b – \sqrt{\Delta}}{2a} = \dfrac{-1}{3}$ et $x_2 = \dfrac{-b + \sqrt{\Delta}}{2a} = \dfrac{1}{6}$.
Ainsi $R(x) = -3 \left (x + \dfrac{1}{3} \right) \left (x – \dfrac{1}{6} \right) $



(x%2B3).png?1556551231149)
_%3D_-3x%C2%B2_-_1_%3A_2_x_%2B_1_%3A_6.png?1556552411203)