Vecteurs directeurs d'une droite et équation cartésienne
Vecteurs directeurs d’une droite et équation cartésienne
Définition
Toute droite du plan possède une équation de la forme $ax + by + c = 0$ (avec $a$ ou $b$ non nul) appelée équation cartésienne de la droite.
Réciproquement, l’ensemble des points $M(x, y)$ tel que $ax + by + c = 0$ (avec $a$ ou $b$ non nul) est une droite.
Par exemple, $5x -2y + 1 = 0$ est une équation cartésienne de droite, cependant $10x -4y + 2 = 0$ est aussi une équation de la même droite : on parle donc d’une équation cartésienne, alors qu’il n’existe qu’une seule équation réduite de droite, que l’on trouve en isolant $y$,
$y = \dfrac{5}{2}x + \dfrac{1}{2}$.
Propriété
Une droite d’équation $ax + by + c = 0$ admet comme vecteur directeur $\overrightarrow{u} \left ( \begin{array}{c} -b \\a \end{array} \right )$
Exemple :
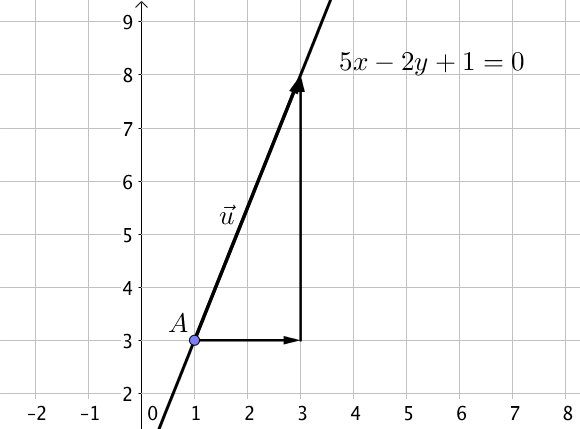
On considère la droite d’équation cartésienne $5x – 2y + 1 = 0$. On souhaite tracer cette droite.
On commence par trouver un vecteur directeur, en appliquant la propriété précédente. $\overrightarrow{u} \left ( \begin{array}{c} 2 \\5 \end{array} \right )$ est un vecteur directeur de la droite.
Il faut ensuite trouver un point appartenant à cette droite.
Pour cela, on choisit une valeur de $x$ quelconque et on calcule la valeur de $y$ correspondante.
Ici, on décide de prendre $x = 1$, et on trouve alors $y = 3$. Le point $A(1; 3)$ appartient donc à la droite.
On place ensuite le point $A$ puis on trace le vecteur directeur à partir de ce point pour obtenir la droite.