Les ondes progressives périodiques
Les ondes progressives périodiques
I. Définition
Une onde progressive est périodique si la perturbation en un lieu donné se répète à intervalles de temps réguliers. On nomme cet intervalle la période, notée $T$. À cette période peut être associée la fréquence, par la relation suivante : $f = \dfrac{1}{T}$ avec $f$ en Hz ou en $\text{s}^{-1}$ et $T$ en s.
II. Onde progressive périodique sinusoïdale
Il s’agit d’une onde progressive périodique dont la perturbation est décrite comme une fonction sinusoïdale du temps.
Concrètement, cette perturbation représente une distance et mathématiquement, la perturbation $u(t)$ est définie par $u(t) = U_0 \times \sin( 2\pi \times f \times t \ (+ \ \phi))$, où $U_0$ est l’amplitude de la déformation et $\phi$ est la phase à l’origine et peut être omise.
La période $T$ est définie comme étant la distance entre deux maxima successifs. L’amplitude $U_0$ est la distance entre le milieu et le maximum (ou le minimum) de l’onde sinusoïdale.
III. Périodicité spatiale et temporelle
Les ondes périodiques ont une double périodicité, à la fois spatiale et temporelle.
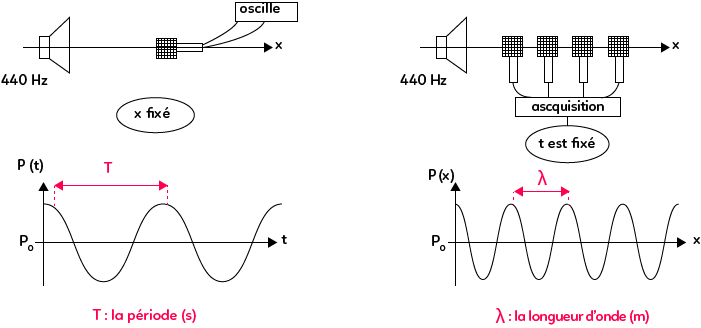
On considère deux haut-parleurs émettant un son périodique sinusoïdal (un son pur) de fréquence $f = 440 \text{ Hz}$. On place devant le premier un microphone à une distance $x$ fixée, alors que devant le second, on place plusieurs microphones à des distances différentes.
Dans le premier cas, la distance étant fixée, on mesure l’évolution de la pression en fonction du temps et on caractérise cette évolution périodique par une période temporelle $T$.
Dans le second cas, l’ensemble des microphones mesure la pression à des positions différentes et donc à un instant donné, on peut établir ce que chacun des microphones mesure. On obtient une évolution périodique, déterminée par une période spatiale $\lambda$, la longueur d’onde (en m).
Il faudra donc prêter une attention particulière à l’unité de l’axe des abscisses pour mesurer la bonne période.
Toutefois, dès lors que l’on connait une des deux périodes, on peut en déduire l’autre par la relation suivante : $\lambda = v \times T $, où $v$ est la célérité de l’onde exprimée en $\text{m.s}^{-1}$, $\lambda$ en m et $T$ en $\text{s}$.
Les ondes progressives périodiques : étude expérimentale
Les ondes progressives périodiques : étude expérimentale
I. La corde
Il s’agit d’une onde progressive périodique souvent sinusoïdale.
Afin de mesurer la période $T$, on utilise un stroboscope qui émet des flashs à une certaine fréquence et donc à intervalles de temps réguliers et on cherche la fréquence maximale pour que la corde soit immobile. Une fois la corde immobilisée, on a donc trouvé la bonne séparation entre deux instants pour que celle-ci revienne dans le même état : c’est la définition même de la période. A partir de la fréquence, on peut trouver la période : $T = \dfrac{1}{f}$.
Pour mesurer la longueur d’onde $\lambda$, on se sert d’une règle graduée et d’un outil permettant de figer la situation à un instant donné, comme un appareil photo par exemple. On mesure ainsi la plus petite distance entre deux points dont les perturbations sont identiques et varient de la même façon, c’est-à-dire deux points ayant le même état vibratoire. Cette plus petite distance correspond à la longueur d’onde $\lambda$.
On peut également se contenter de trouver une des deux périodes et d’utiliser la relation qui suit pour déterminer la période manquante : $\lambda = v \times T $, où $v$ est la célérité de l’onde exprimée en $\text{m.s}^{-1}$, $\lambda$ en m et $T$ en s.
II. La cuve à onde
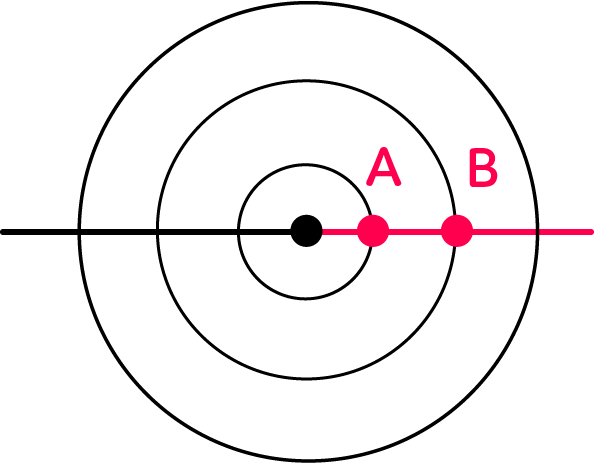
Il s’agit d’une cuve remplie d’eau à la surface de laquelle il y a un excitateur ponctuel, c’est-à-dire une pointe qui oscille verticalement et périodiquement, créant ainsi des ondes circulaires qui se propagent.
Pour obtenir la période $T$, on effectue la même démarche que pour le cas de la corde.
Si on souhaite connaître la longueur d’onde $\lambda$, on prend une photo de la cuve et on cherche deux points dans le même état vibratoire, en se fiant aux couleurs de la photo (on pourra par exemple choisir deux points dans deux zones claires successives). La distance séparant les deux points est la longueur d’onde recherchée.
Onde mécanique progressive
Onde mécanique progressive
I. Onde progressive
Une onde progressive est la propagation dans le temps et dans l’espace d’une perturbation ou d’une déformation.
Exemples :
– La déformation d’une corde : on agite une corde à une extrémité, la déformation va alors se propager le long de la corde (dans l’espace) et au cours du temps.
– Une onde sismique : la terre vibre, la perturbation est la déformation de la terre qui se propage.
– Une onde sonore : la perturbation est la déformation de l’air entre les mains et l’oreille.
II. Célérité et retard
La célérité $v$
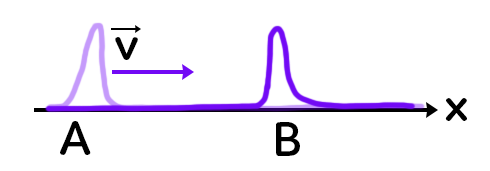
La célérité, notée $c$ ou $v,$ est la vitesse de propagation de la perturbation au cours du temps.
On peut calculer la vitesse de propagation entre le point $A$ et $B,$ en utilisant une formule déjà connue : $v=\dfrac{d}{t}$
Ici $ v = \dfrac{AB}{t}$
Le retard $\tau$
Le retard est un temps (en secondes).
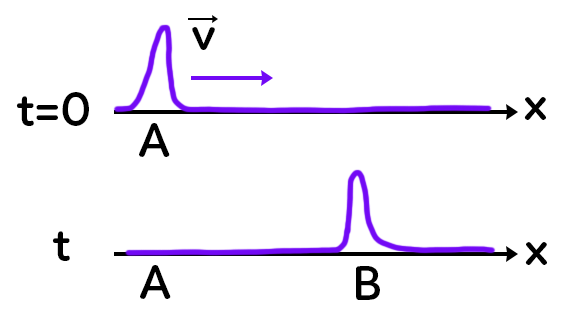
On voit que la perturbation en $B$ à l’instant $t=\tau$ est la même que celle qui était en $A$ à l’instant $ t=0$.
Ce retard $\tau$ vaut alors $\tau=\dfrac{AB}{v}$