Méridiens et parallèles
Méridiens et parallèles
I. Les méridiens
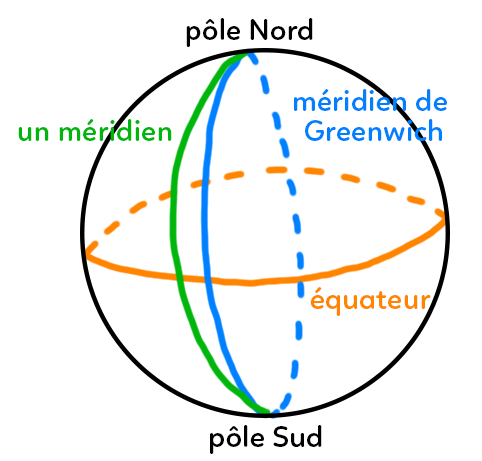
Les méridiens sont des demi-cercles imaginaires qui passent par les pôles Nord et Sud.
Le méridien de référence est le méridien de Greenwich, celui-ci permet de calculer ensuite les longitudes.
La longitude est l’angle $widehat{MOG}$ sur le schéma ; $M$ appartient au méridien qui nous intéresse et à l’équateur, $G$ appartient au méridien de Greenwich et à l’équateur et $O$ est le centre de la Terre.
Tous les méridiens ont la même longueur car ce sont tous des demi-cercles dont le rayon vaut le rayon de la Terre. La longueur d’un méridien est égale à la moitié de la circonférence de la Terre. Ainsi on a $frac{2 pi R_T}{2}= pi R_T simeq 20 000 km $
(Le rayon de la Terre vaut $R_T simeq 6 380 km$.)
II. Les parallèles
Les parallèles sont des cercles imaginaires contenus dans un plan parallèle au plan de l’équateur.
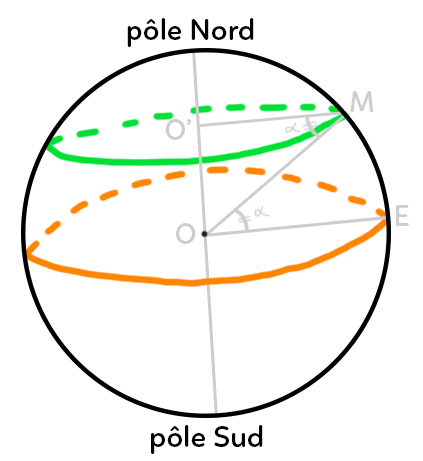
Un parallèle est repéré par sa latitude $alpha = widehat{EOM} = widehat{OMO’}$.
Les angles $widehat{OMO’}$ et $widehat{EOM}$ sont des angles alternes-internes car les droites $O’M$ et $OE$ sont parallèles, ils sont donc égaux.
III. Coordonnées géographiques
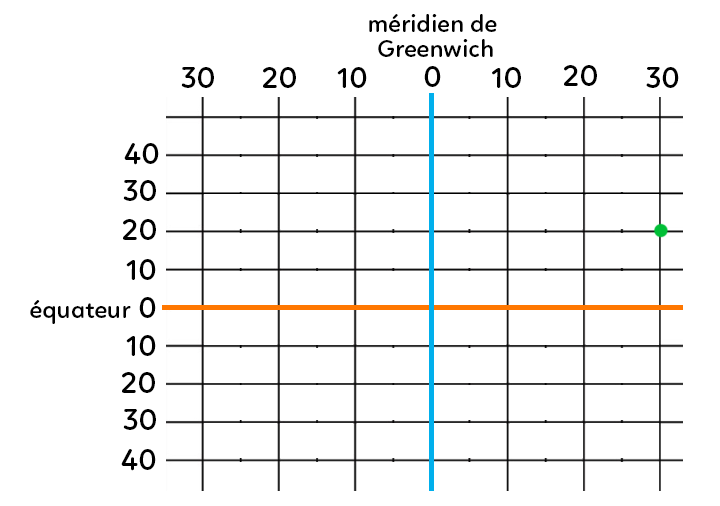
On explique ici comment se repérer si on ne connaît que les latitudes et les longitudes. On utilise un tableau de ce type :
Par exemple : où se trouve le point de latitude 20° Nord et de longitude 30° Est ?
Il suffit de se placer sur les bonnes droites du tableau : la ligne 20 en haut pour les latitudes (lignes) et la ligne 30 à droite pour les longitudes (colonnes), voir point vert.
Calculs sur les parallèles
Calculs sur les parallèles
I. La longueur d’un parallèle
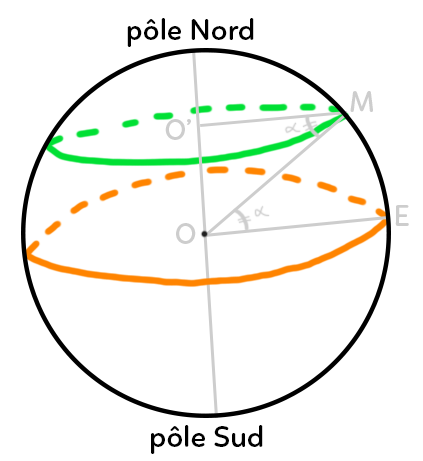
Dans ce schéma, il y a un parallèle représenté en vert et l’équateur représenté en orange. L’angle alpha se retrouve à deux endroits car on a des angles alternes-internes. Alpha étant la latitude.
Un parallèle est un cercle imaginaire. Sa longueur est donc la circonférence du cercle, dont la formule générale à connaître est : $l = 2pi r$, avec $r$ le rayon.
Le rayon n’est pas le même pour le parallèle et pour l’équateur, étant donné la forme sphérique de la Terre. On cherche à exprimer ce rayon, donc la distance : $O’M$. On a $2times pi times O’M$ avec $O’M$ exprimé en fonction des autres grandeurs sur le schéma.
Le triangle $OO’M$ est rectangle en $O’$ et on peut donc dire que dans ce triangle, le cosinus de alpha est égal à :
$dfrac{côté adjacent}{hypothénuse}=dfrac{O’M}{OM}$.
On peut en déduire la longueur $O’M$, le rayon du parallèle. Donc : $O’M = OMtimes cos(alpha)$.
On introduit cette notion dans l’équation de la longueur du parallèle : $l = 2times pi times R_Ttimes cos(alpha)$.
On a alors l’expression pour laquelle on va pouvoir faire une application numérique. Par exemple, si on a 60° de latitude Nord, alors : $l = 2pitimes 6 380times cos(60) = 20 033 km.$
II. Calcul de la longueur d’un arc de parallèle
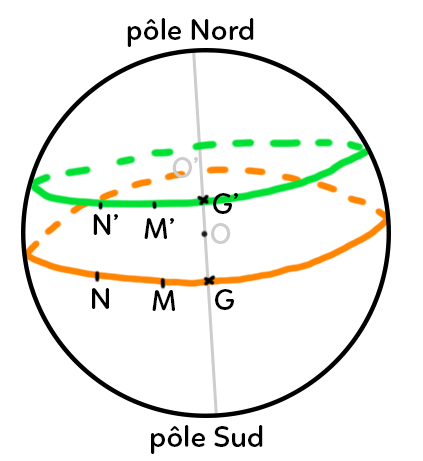
On considère deux points situés sur un même parallèle, de longitude respective 60° Ouest et 10° Ouest. On a schématisé la situation avec le parallèle et les deux points considérés sont $M’$ et $N’.$
On a représenté l’équateur avec les projetés de $N’$ et $M’$ sur l’équateur ce qui donne les points $N$ et $M.$ Par définition, une longitude c’est l’angle, par exemple $widehat{MOG}$ pour le point $M$ et l’angle $widehat{NOG}$ pour le point $N.$
D’après le schéma, on voit que les angles $widehat{MOG}$ et $widehat{M’O’G’}$ sont les mêmes. De même pour les angles $widehat{N’O’G’} et widehat{NOG}$. Donc, les longitudes s’écrivent : $widehat{N’O’G’}$ pour $N’$ et $widehat{M’O’G’}$ pour $M’.$
Donc, la différence entre ces deux longitudes donne l’angle $widehat{N’O’M’}$. C’est l’angle qui va intercepter l’arc de cercle $N’M’.$ Cela est égal à la différence entre les deux longitudes données : $60-10 = 50°$.
Or la longueur d’un arc est proportionnelle à l’angle qui l’intercepte. On construit un tableau de proportionnalité avec l’angle et la longueur de l’arc :
| Angle (°) | $350$ | $50$ |
| Longueur de l’arc (m) | $2 pi times O’M’$ | l |
Pour 360°, c’est-à-dire un tour complet, on a la circonférence du cercle c’est-à-dire $2pi r$. Ici, $2pi times O’M’$. On va chercher la longueur de l’arc $N’M’$. On l’appelle $l$. L’angle qui intercepte l’arc est de 50°.
On résout ensuite le tableau de proportionnalité : $l = dfrac{2pi times O’M’times 50}{360}$.
On fera ensuite l’application numérique lorsque l’on aura des valeurs.
Calcul sur la longueur d'un méridien par la méthode d'Ératosthène
Calcul sur la longueur d’un méridien par la méthode d’Ératosthène
L’expérience d’Ératosthène
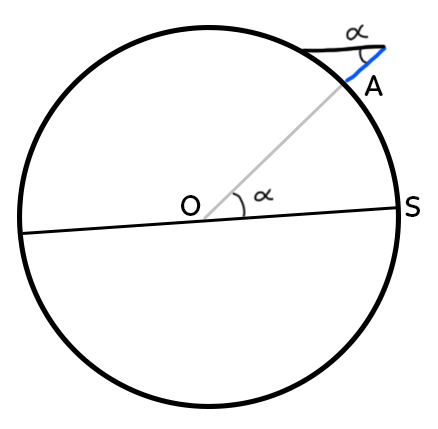
Ératosthène était un savant grec de l’Antiquité qui fut l’un des premiers à déterminer la circonférence de la Terre. Pour cela, il a réalisé deux expériences identiques dans deux villes différentes : Syren (S) et Alexandrie (A).
Il a constaté qu’à Syren, le 21 juin, les rayons arrivent à la verticale du sol, c’est-à-dire que leur trajectoire passe par le centre de la Terre. On va donc s’orienter sur la droite $(SO)$. Cela n’est pas le cas à Alexandrie. Les rayons ne sont pas orientés vers le centre de la Terre. Eratosthène a mesuré l’angle formé entre le phare et la droite $(AC)$.
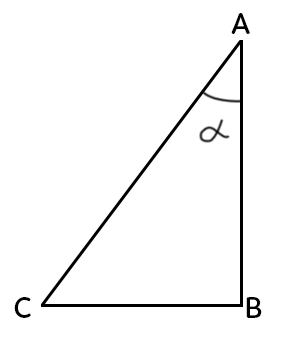
Sur ce schéma, dans le triangle $ABC$, $AB$ est le phare, $BC$ l’ombre du phare et donc $alpha$ l’angle formé par la droite $(AC)$ et $(AB)$.
Il a mesuré un angle de 7,2°. Or, cet angle $alpha$ on le retrouve aussi entre les points $S, O$ et $A,$ car ce sont des angles alternes internes. Comme on sait que l’angle qui intercepte l’arc est proportionnel à la longueur de cet arc, il a pu ainsi déterminer la circonférence de la Terre.
Par un tableau de proportionnalité, on voit que 7,2° va correspondre à la distance entre Syren et Alexandrie, qui est estimée à 5 000 stades. Un stade étant égal à 157,5 mètres.
| Angle (°) | $360$ | $7,2$ |
| Longueur de l’arc (m) | $2 pi r$ | $5000$ stades |
On cherche la longueur de la Terre pour 360°. On résout ce tableau de proportionnalité en faisant le calcul. $2pi r = dfrac{5000times 0,1575 times 360}{7,2} = 39 375$km. Cela est très proche de la valeur connue actuellement.