Fonctions composées - exp(u(x))
Fonctions composées
Soit $u(x)$ une fonction continue et dérivable sur $\mathbb{R}$, la fonction $f(x)=e^{u(x)}$ a pour dérivée
$f'(x)=u'(x)e^{u(x)}$.
Exemple
Soit $g$ la fonction définie et dérivable sur $\mathbb{R}$ par :
$g(x)=e^{(-3x^2+x)}$.
Déterminons sa dérivée.
On pose : $u(x)= -3x^2+x$.
On a donc : $u'(x)=-6x+1$.
On a : $g'(x)= u'(x)e^{u(x)}$.
Soit : $g'(x)=(-6x+1)e^{(-3x^2+x)}$.
Autre exemple
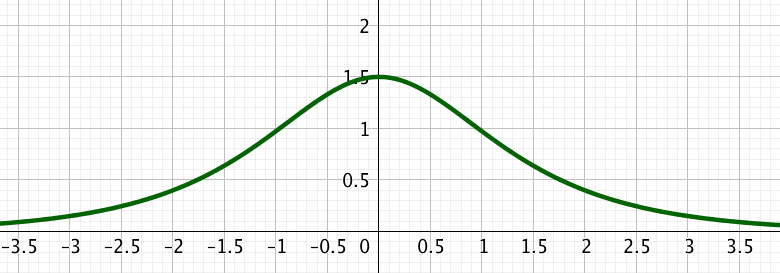
Etudier les variations de la fonction $f(x)$= $\displaystyle \frac{3e^x}{e^{2x}+1}$.
étape 1 : On cherche toujours l’ensemble de définition d’une fonction.
$Df= \mathbb{R} $ car $e^{2x}$ ne peut être égal à $-1$, c’est toujours positif.
étape 2 : On cherche les limites aux bornes de l’ensemble de définition : en $+\infty$ et en $-\infty$.
On factorise par $e^x$ et on simplifie pour lever l’indétermination.
$\displaystyle \lim \limits_{x \rightarrow +\infty}f(x)=\lim \limits_{x \rightarrow +\infty}\frac{e^x\times 3}{e^{x}(e^{x}+\displaystyle\frac{1}{e^{x}})}=\lim \limits_{x \rightarrow +\infty}\frac{3}{e^{x}+\displaystyle\frac{1}{e^{x}}}=0$ car
$\displaystyle \lim \limits_{x \rightarrow +\infty}e^x+\frac{1}{e^x}=+\infty$
$\displaystyle \lim \limits_{x \rightarrow -\infty}f(x)=\lim \limits_{x \rightarrow -\infty}\frac{3}{e^{x}+\displaystyle\frac{1}{e^{x}}}=0$ car
$\displaystyle \lim \limits_{x \rightarrow -\infty}e^x+\frac{1}{e^x}=+\infty$
étape 3 : On dérive $f$ comme quotient de fonctions dérivables sur $\mathbb{R}$.
On utilise la formule suivante :
$\displaystyle (\frac{u}{v})’=\frac{u’v-uv’}{v^2}$.
$\displaystyle u(x)=3e^x, u'(x)=3e^x \hspace{0.2cm} \text{et} \hspace{0.2cm} v(x)=e^{2x}+1, v'(x)= 2e^{2x}$
$\displaystyle f'(x)= \frac{3e^x (e^{2x}+1)-3e^x (2e^{2x})}{(e^{2x}+1)^2}$
$\displaystyle f'(x)= \frac{3e^x (1-e^{2x})}{(e^{2x}+1)^2}$
On remarque que $(1-e^{2x})$ est une égalité remarquable égale à $(1-e^x)(1+e^x)$.
Le signe de $f'(x)$ est du signe de $(1-e^x)(1+e^x)$ donc de $(1-e^x)$.
On a :
$(1-e^x)\geq 0 \iff 1\geq e^x \iff 0\geq x$
On en déduit le tableau de variations :
Définition de l'intégrale - Exercice
Calculons \(I = \int_{1}^4 x dx = \int_{1}^4 t dt\).
Étape 1 : On repère l’aire recherchée.
Étape 2 : On remarque qu’il s’agit d’un trapèze rectangle.
Étape 3 : La formule du calcul d’aire du trapèze rectangle est connue. On peut l’utiliser pour calculer l’intégrale :
\( A = \frac{(B + b) \times h}{2}\).
Opérations sur les primitives
Opérations élémentaires sur les primitives
Propriétés
Soit $u$ et $v$ deux fonctions dérivables sur un intervalle $I$ réel.
| Fonction | Une primitive | Conditions |
| $u’+v’$ | $u+v$ | |
| $ku’$ (avec $k$ constante) | $ku$ | |
| $u’u^n$ avec $n$ appartient à $\mathbb{Z}$ et différent de $-1$ | $\dfrac{u^{n+1}}{n+1}$ | $u$ différent de $0$ sur $I$ si $u\leq 0$ |
| $\dfrac{u’}{\sqrt u}$ | 2$\sqrt u$ | $u>0$ sur $I$ |
| $\dfrac{v’}{v^2}$ | $-\dfrac{1}{v}$ | $v\neq 0$ sur $I$ |
| $u’e^{u}$ | $e^{u}$ | |
| $\dfrac{u’}{u}$ |
$\ln(u)$ $\ln(-u)$ |
$u>0$ sur $I$ $u<0$ sur $I$ |
| $u'(v’\circ u)$ | $v\circ u$ |
Exemples
1. Chercher une primitive sur \(\mathbb{R}\) de : $ f(x) = x e^{x^2+ 1}$
2. Chercher une primitive sur \(\mathbb{R}\) de : $ g(x) = \dfrac{6x + 3}{x^2 + x + 1}$.
Correction
1. $ f(x) = x e^{x^2+ 1}$
Etape 1 : On cherche les expressions de \(u\) et \(u’\) pour arriver à la forme \(u’ e^u\).
\(u (x) = x^2+ 1 \) et \(u'(x)= 2x \)
Etape 2 : On multiplie par $2$ et par $\dfrac{1}{2}$ pour faire apparaître le “$2$” manquant.
$ f(x)=\dfrac{1}{2} \times 2x e^{x^2+ 1} $
$ f(x)=\dfrac{1}{2} u'(x) e^u(x) $
Etape 3 : On définit une primitive grâce au cours.
$ F(x)= \dfrac{1}{2} e^{x^2+ 1}$
2.$ g(x) = \dfrac{6x + 3}{x^2 + x + 1}$
Etape 1 : On note \(u(x)= x^2 + x + 1 \) et \(u'(x)=2x+1\). On factorise par $3$ le numérateur pour faire apparaître \(u'(x)\).
On a : $ g(x) = \dfrac{3(2x + 1)}{x^2 + x + 1}$.
Soit : $ g(x) = \dfrac{3u'(x)}{u(x)}$.
Etape 2 : On remarque que $x^2+x+1>0$ sur $\mathbb{R}$ et on définit une primitive de $g$ grâce au cours.
$ G(x) = 3\ln (x^2 + x + 1)+ c$
Calculs d'intégrales
Calculs d’intégrales
Propriété
Soit $f$ une fonction continue sur un intervalle $I$.
Soit $F$, une primitive de \(f\) sur $I$.
Pour tous réels $a$ et $b$ de l’intervalle $I$, on a :
$\displaystyle\int_{a}^b f(t) dt= F(b)- F(a) $ que l’on note aussi
$\displaystyle\int_{a}^b f(t) dt=\left[F(t)\right]_{a}^b$
Exemples
Calculer :
$I$=\(\displaystyle\int_{1}^2 \dfrac{x^2+3x+1}{x^2}dx\).
$J$=\(\displaystyle \int_{0}^1 x(2x^2-1)^3 dx\).
Correction
Calcul de $I$
Étape 1 : La fonction $f(x)= \dfrac{x^2+3x+1}{x^2}$ est définie et continue sur $[1;2]$.
On décompose l’expression en trois fractions de dénominateur commun.
$I$=\(\displaystyle\int_{1}^2 (\dfrac{x^2}{x^2}+\dfrac{3x}{x^2}+\dfrac{1}{x^2})dx\)
$I$=\(\displaystyle\int_{1}^2 (1+\dfrac{3}{x}+\dfrac{1}{x^2})dx\)
$I$=\(\displaystyle\int_{1}^2 dx+ \int_{1}^2\dfrac{3}{x}dx+ \int_{1}^2\dfrac{1}{x^2}dx\)
Étape 2 : On peut définir des primitives de chaque expression.
$I$= \(\displaystyle \left[x+3\ln x-\dfrac{1}{x}\right]_{1}^2\)
Étape 3 : On calcule $F(2)-F(1)$.
$I$= \(\displaystyle (2+3\ln 2-\dfrac{1}{2})-(1+3\ln 1-\dfrac{1}{1})\)
$I$= \(\displaystyle \dfrac{3}{2}+3\ln 2 \) (unité d’aire).
Calcul de $J$
On pose : $u(x)=2x^2-1$ et $u'(x)=4x$.
On modifie l’expression pour la faire apparaître sous la forme $u’\times u^3$.
$J$=\(\displaystyle \dfrac{1}{4} \int_{0}^1 4x(2x^2-1)^3 dx \)
$J$=\(\displaystyle \dfrac{1}{4}\left[\dfrac{1}{4}(2x^2-1)^4\right]_{0}^1 \)
$J$=\(\displaystyle \dfrac{1}{4}\left((\dfrac{1}{4}(1)^4)-(\dfrac{1}{4}(-1)^4)\right)\)
$J$=\(\displaystyle \dfrac{1}{4}\left(\dfrac{1}{4}-\dfrac{1}{4}\right)\)
$J$= $0$