Fonctions convexes et concaves
Fonctions convexes et concaves
Définition
Soit $f$ une fonction dérivable sur un intervalle $I$,
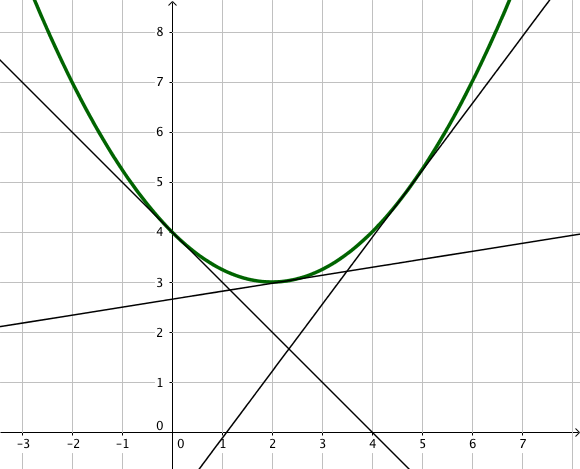
$f$ est convexe sur $I$ lorsque sa courbe est entièrement située au dessus de chacune de ses tangentes.
Il s’agit donc d’une notion locale, définie sur un intervalle.
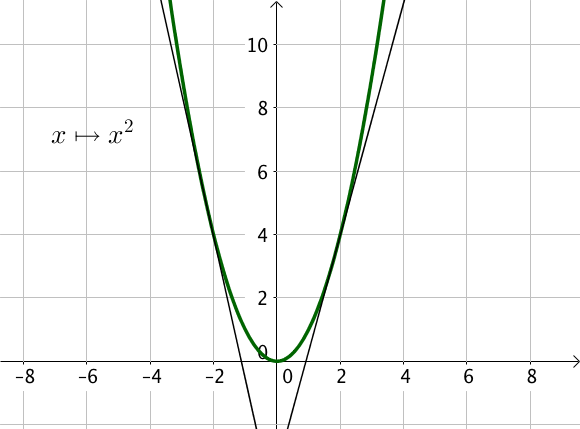
Par exemple, la fonction $y = x^2$ est convexe sur $\mathbb{R}$.
Pour démonter la convexité d’une fonction, on utilisera d’autres propriétés plus efficaces que cette notion graphique.
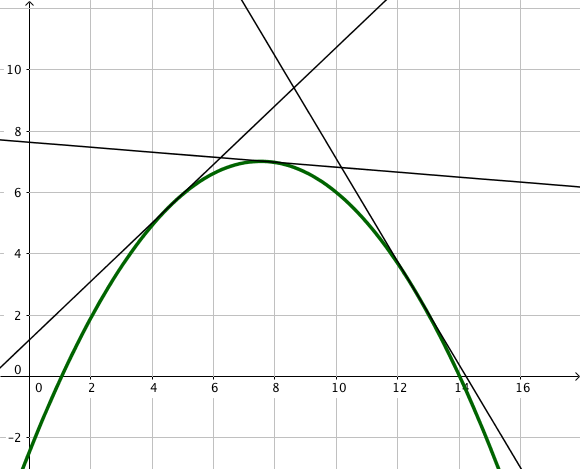
$f$ est concave sur $I$ lorsque sa courbe est entièrement située en dessous de chacune de ses tangentes.
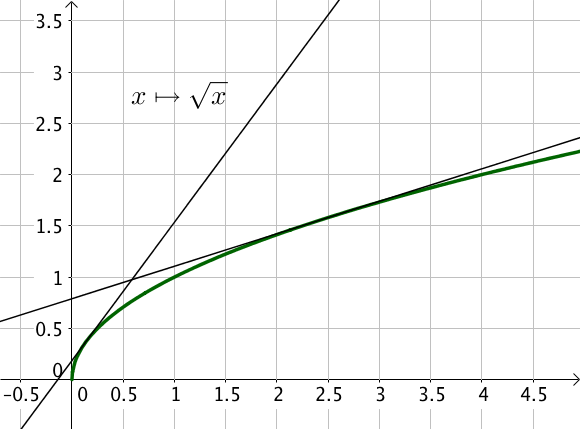
Par exemple, la fonction $y= \sqrt{x}$ est concave sur $\mathbb{R}^+_*$
Convexité des fonctions de référence
Convexité des fonctions de référence
Il s’agit d’apprendre parmi les fonctions usuelles lesquelles sont convexes et lesquelles sont concaves.
1) Fonctions convexes
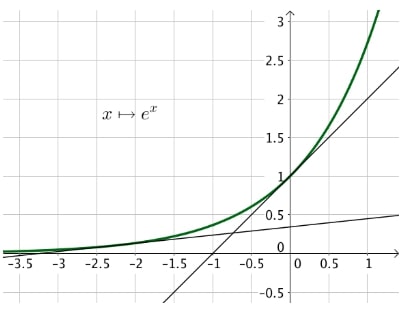
Les fonctions $x \mapsto x^2$ et $x \mapsto e^x$ sont des fonctions convexes sur $\mathbb{R}$.
Fonction exponentielle :
En effet, en reprenant la définition d’une fonction convexe, on peut vérifier que les courbes représentatives de ces deux fonctions sont au-dessus de chacune de leurs tangentes.
2) Fonctions concaves
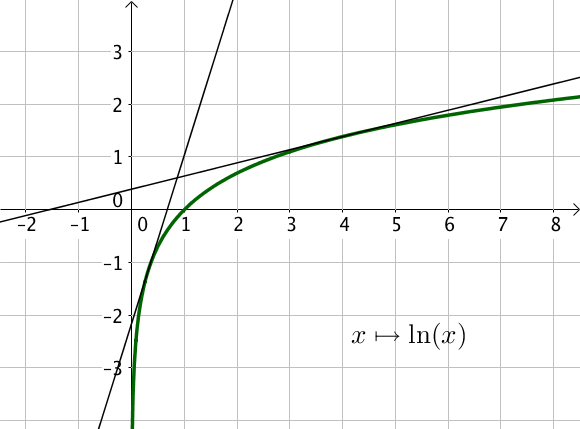
Les fonctions $x \mapsto \sqrt{x}$ et $x \mapsto \ln(x)$ sont des fonctions concaves sur $\mathbb{R}^+_*$.
La fonction racine carrée n’est pas dérivable en $0$, or la notion de convexité nécessite la dérivabilité de la fonction sur l’intervalle d’étude, donc la fonction racine carrée est uniquement concave sur $]0; +\infty [$.
On peut à nouveau vérifier graphiquement que les courbes sont en dessous de leurs tangentes.
Étude de la convexité d'une fonction
Étude de la convexité d’une fonction
Il existe deux principaux théorèmes permettant d’étudier l’éventuelle convexité ou concavité d’une fonction.
Théorème 1 :
Soit $f$ une fonction dérivable sur $I$,
1) $f$ est convexe sur $ I \ \iff \ f’$ est croissante sur $I$
2) $f$ est concave sur $ I \ \iff \ f’$ est décroissante sur $I$
Pour étudier la convexité d’une fonction, il suffit d’étudier les variations de sa dérivée.
Exemple :
Etudions la fonction $f(x) = x^2 -3x +2$ sur l’intervalle $I = \mathbb{R}$.
$f$ est une fonction polynôme, elle est donc dérivable sur $\mathbb{R}$ et $\ f'(x) = 2x – 3$.
La dérivée de $\ f$ est une fonction affine. Le cours permet de conclure que $\ f’$ est croissante car $2>0$.
Ainsi, comme $\ f’$ est croissante sur $I$, $f$ est convexe sur $I$.
Théorème 2 :
Soit $f$ une fonction dérivable sur $I$ et on suppose de plus que $\ f”$ existe sur $I$ ($f”$ est la dérivée de la dérivée : c’est la dérivée seconde de $f$),
1) si pour tout $x \in I, \ f”(x) \geq 0$, alors $\ f$ est convexe sur $I$
2) si pour tout $x \in I, \ f”(x) \leq 0$, alors $\ f$ est concave sur $I$
Ces deux théorèmes sont liés.
En effet, si on suppose que $\ f”(x) \geq 0$, cela implique que $\ f’$ est croissante et dans les deux cas, $f$ est convexe.
Exemple :
Soit $f(x) = x^2$, on veut démontrer que $f$ est convexe sur $\mathbb{R}$.
Soit $x \in \mathbb{R}$, on calcule dans un premier temps $\ f'(x) = 2x$ puis la dérivée seconde $\ f”(x) = 2 \geq 0$.
Ainsi, pour tout $x \in \mathbb{R}, \ f”(x) \geq 0$, donc $f$ est convexe sur $\mathbb{R}$.