Dérivée seconde et position d'une courbe par rapport à ses tangentes
Dérivée seconde et position d’une courbe par rapport à ses tangentes
Soit $f$ une fonction deux fois dérivable sur un intervalle $I$ et $x_0 \in I$.
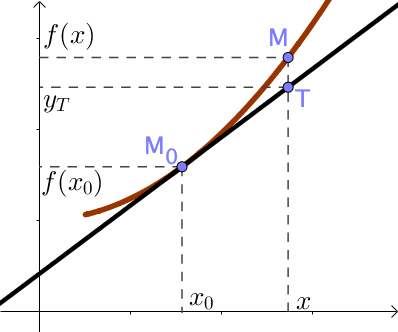
Soit $\Gamma_f$ la courbe représentative de la fonction $f$ dans le repère $(O; \overrightarrow{i}; \overrightarrow{j})$ et $M_O(x_0, f(x_0))$.
On note $\Delta$ la tangente à $\Gamma_F$ en $M_0$ (cette tangente existe car $f$ est dérivable en $x_0$).
Soit $x \in I$ et $M(x, f(x))$,
Soit $T$ le point de $\Delta$ tel que $T(x, y_T)$,
On étudie ici la position de la courbe par rapport à sa tangente en un point d’abscisse $x_0$ quelconque. Pour cela, on étudie l’ordonnée du vecteur $\overrightarrow{TM}$ (l’abscisse du vecteur étant nulle) à partir d’un point $M$ quelconque :
$y_\overrightarrow{TM} = y_M – y_T = f(x) – y_T$.
Or $T$ est un point de la tangente $\Delta$ dont on connait l’équation :
$y = f(x_0) + (x – x_0)f'(x_0)$.
Ainsi, $y_T = f(x_0) + (x – x_0)f'(x_0)$.
Finalement, $y_\overrightarrow{TM} = f(x) – f(x_0) – (x – x_0)f'(x_0)$.
On note alors $\delta(x) = f(x) – f(x_0) – (x – x_0)f'(x_0)$ et on étudie le signe de cette fonction. Pour cela, on étudie ses variations. La fonction $\delta$ est dérivable sur $I$ en tant que somme de fonctions dérivables sur $I$ :
$\delta'(x) = f'(x) – f'(x_0)$.
Pour étudier le signe de $\delta'(x)$, on fait tout d’abord l’hypothèse que $f” \geq 0$ sur $I$, c’est à dire que $f’$ est croissante sur $I$.
Ainsi, pour $x \geq x_0, \, f'(x) \geq f'(x_0)$ c’est à dire $\delta'(x) \geq 0$.
De même, pour $x \leq x_0, \, f'(x) \leq f'(x_0)$ c’est à dire $\delta'(x) \leq 0$.
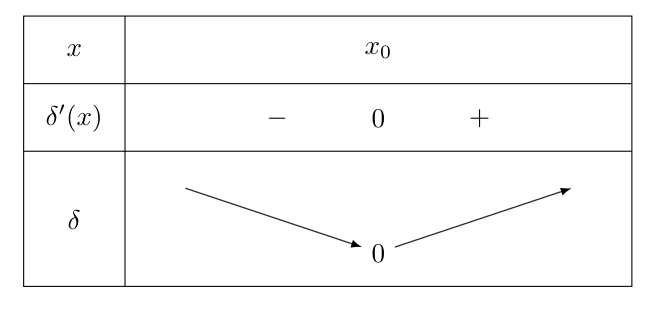
On en déduit alors le sens de variation de la fonction $\delta$.
$\delta$ est décroissante pour $x \leq x_0$ et croissante pour $x \geq x_0$.
En outre, $\delta(x_0) = f(x_0) – f(x_0) – (x_0 – x_0)f'(x_0) = 0$.
Finalement, $\delta \geq 0$ ce qui signifie que l’ordonnée de $\overrightarrow{TM}$ est positive et donc que $M$ est au dessus de $T$.
Puisque ce raisonnement peut être fait pour tout $x_0 \in I$, on en déduit que lorsque $f” \geq 0$, la courbe est toute entière située au dessus de toutes ses tangentes. On dit que $f$ est convexe.
De même, on peut s’intéresser à l’hypothèse de $f” \leq 0$ sur $I$, c’est à dire que $f’$ est décroissante sur $I$.
Ainsi, pour $x \geq x_0, \, f'(x) \leq f'(x_0)$ c’est à dire $\delta'(x) \leq 0$.
De même, pour $x \leq x_0, \, f'(x) \geq f'(x_0)$ c’est à dire $\delta'(x) \geq 0$.
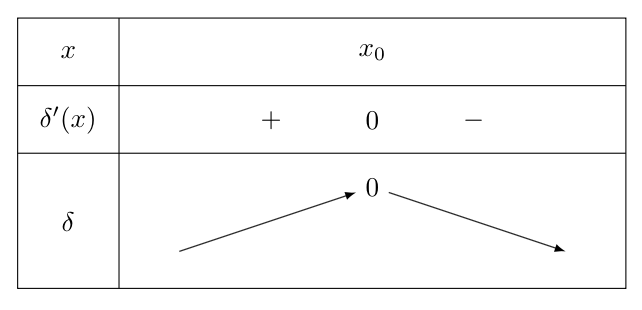
On en déduit alors le sens de variation de la fonction $\delta$.
Ainsi, $\delta \leq 0$ et $M$ est sous $T$.
Puisque ce raisonnement peut être fait pour tout $x_0 \in I$, on en déduit que lorsque $f” \leq 0$, la courbe est toute entière située en dessous de toutes ses tangentes. On dit que $f$ est concave.
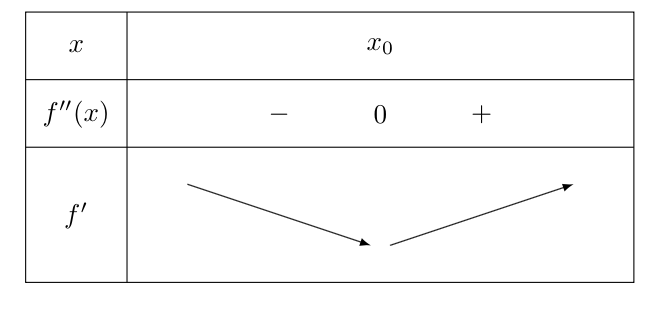
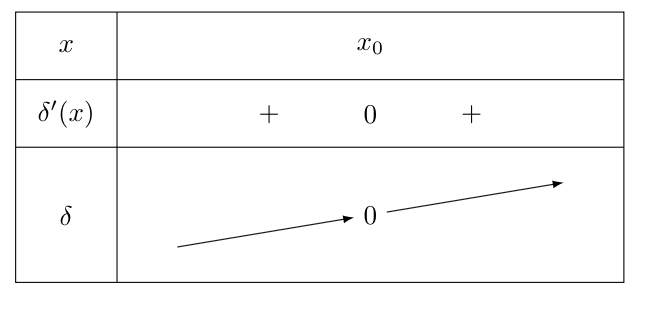
Le dernier cas que l’on peut traiter correspond au cas où $f”$ n’est pas de signe constant sur $I$ et s’annule en $x_0$ en changeant de signe. On se propose ici de traiter le cas où $f”$ est d’abord négative puis positive.
Ainsi, $f'(x) \geq f'(x_0)$ pour tout $x \in I$. Donc $\delta’ \geq 0$. Ainsi $\delta$ est croissante sur $I$.
Or $\delta$ s’annule en $x_0$. Donc pour $x \leq x_0$, $\delta$ est négative. Et pour $x \geq x_0$, $\delta$ est positive.
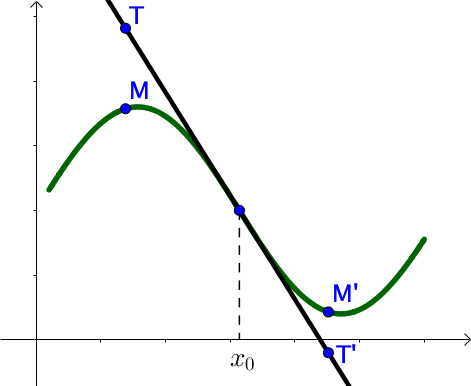
Graphiquement, pour $x \leq x_0$ la courbe de $f$ est en dessous de ses tangentes.
Pour $x \geq x_0$, la courbe de $f$ est au-dessus de ses tangentes.
Ainsi, si $f”$ s’annule en changeant de signe en $x_0$, $\Gamma_f$ traverse sa tangente en $M_0$.
On dit que $x_0$ est un point d’inflexion de $f$.
Dérivée seconde d'une fonction
Dérivée seconde d’une fonction
Définition
Soit $f$ une fonction dérivable sur un intervalle $I$ de $\mathbb{R}$.
Si $f’$ est dérivable sur $I$, on note $(f’)’ =f”$ sa dérivée que l’on appelle dérivée seconde de $f$ sur $I$.
Exemples :
- Soit $f : x \mapsto 3x^2 + 5x + 7$ une fonction polynomiale, définie et dérivable sur $\mathbb{R}$.
Soit $x \in \mathbb{R}$, $f'(x) = 6x + 5$
$f’$ est aussi une fonction polynomiale, elle est donc dérivable sur $\mathbb{R}$.
Soit $x \in \mathbb{R}$, $f”(x) = 6$
- Soit $g: x \mapsto \cos(5x + 3)$ une fonction définie sur $\mathbb{R}$ et dérivable sur $\mathbb{R}$ en tant que composée de deux fonctions dérivables sur cet intervalle.
Soit $x \in \mathbb{R}$, $g'(x) = -5\sin(5x + 3)$.
$g’$ est aussi dérivable en tant que composée de deux fonctions dérivables sur $\mathbb{R}$.
Ainsi, soit $x \in \mathbb{R}$, $g”(x) = -25\cos(5x + 3)$.
Propriétés
Soit $\lambda \in \mathbb{R}$,
Si $u$ et $v$ sont dérivables deux fois sur $I$,
Alors $(\lambda u + v)$ et $(uv)$ sont deux fois dérivables sur $I$.
Les formules de la dérivée seconde du produit et de la somme ne sont pas à connaitre.