Dérivation des fonctions trigonométriques
Dérivation de fonctions trigonométriques
Propriétés
Soient $a$ et $b$ deux réels.
Pour tout $x\in \mathbb{R},$
$(\cos(ax+b))’=-a\sin(ax+b)$
$(\sin(ax+b))’=a\cos(ax+b)$
En particulier, pour $a=1$ et $b=0$,
Pour tout $x\in \mathbb{R},$
$(\cos(x))’=-\sin(x) $
$(\sin(x))’=\cos(x) $
Exemples
Dériver les fonctions suivantes en précisant leurs ensembles de dérivabilité :
1) $f(x)=\dfrac{\sin(x)}{\cos(x)}$ sur $\left] -\dfrac{\pi}{2},\dfrac{\pi}{2} \right[$
2) $g(x) = \dfrac{\sin(3-2x)}{2}$ sur $\mathbb{R}$
3) $k(x)= \sin(x)\cos(x)$ sur $\mathbb{R}$
Correction
1) $f$ est dérivable sur $\left] -\dfrac{\pi}{2},\dfrac{\pi}{2} \right[$ en tant que quotient de fonctions dérivables sur $\left] -\dfrac{\pi}{2},\dfrac{\pi}{2} \right[$ avec $\cos(x)$ non nul sur cet intervalle.
On écrit $u(x)=\sin(x)$ et $v(x)=\cos(x)$ de sorte que $f(x)=\dfrac{u(x)}{v(x)}$.
On a alors $u'(x)=\cos(x)$ et $v'(x)=-\sin(x)$ et pour tout $x\in \left] -\dfrac{\pi}{2},\dfrac{\pi}{2} \right[$ :
$ f'(x) = \dfrac{u'(x)v(x)-u(x)v'(x)}{v^2(x)}$
$f'(x)= \dfrac{\cos^2(x)+\sin^2(x)}{\cos^2(x)}$
$f'(x)=\dfrac{1}{\cos^2(x)}$
2) Pour $x\in\mathbb{R}$ :
$ g'(x) = -2\cos(3-2x)\times \dfrac12$
soit $ g'(x) = -\cos(3-2x)$
3) $k$ est dérivable sur $\mathbb{R}$ en tant que produit de fonctions dérivables sur $\mathbb{R}$.
On écrit $u(x)=\cos(x)$ et $v(x)=\sin(x)$ de sorte que $k(x)=u(x)v(x)$
On a alors : $u'(x)=-\sin(x)$ et $v'(x)=\cos(x)$.
Ainsi, pour $x\in\mathbb{R}$ :
$ k'(x) = u'(x)v(x)+u(x)v'(x)$
$ k'(x)=-\sin^2(x)+\cos^2(x) $
$ k'(x)= 2\cos^2(x)-1$
$ k'(x)=\cos(2x)$
Inéquations trigonométriques
Inéquations trigonométriques
Résolution graphique
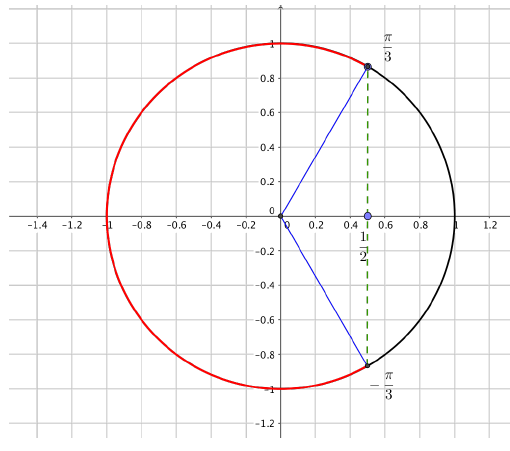
On souhaite résoudre sur $[0,2\pi]$ l’inéquation suivante : $\cos(x)\leqslant \dfrac12$.
On sait que $\cos\left(\dfrac{\pi}{3}\right)=\dfrac12$ et $\cos\left(-\dfrac{\pi}{3}\right)=\dfrac12$.
Ici, on veut résoudre l’équation sur $[0,2\pi]$ donc on écrit
$-\dfrac{\pi}{3}=-\dfrac{\pi}{3}+2\pi= \dfrac{5\pi}{3}$ $[2\pi]$.
On constate alors que tous les $x$ compris dans la zone surlignée en rouge ont un cosinus inférieur à $\dfrac12$.
Ensemble de solutions
On peut alors simplement donner l’ensemble de solutions de l’inéquation de départ :
$ \mathcal{S}= \left[ \dfrac{\pi}{3};\dfrac{5\pi}{3} \right]$