Linéarité de l'espérance.
Linéarité de l’espérance
Propriétés :
Soit $X$ une variable aléatoire qui prend les valeurs $x_i$, de probabilités $p_i$ et Y, les valeurs $y_i$, de probabilités $q_i$ pour $i$ variant de $1$ à $n$,
Soit $a \in \mathbb{R}$,
On a :
$\mathbb{E}(X + Y) = \mathbb{E}(X) + \mathbb{E}(Y)$
$\mathbb{E}(aX) = a\mathbb{E}(X)$
On dit que l’espérance est linéaire.
Démonstration :
Soit $a \in \mathbb{R}$,
Par définition de l’espérance mathématique,
$\mathbb{E}(X) = \displaystyle \sum_{i=1}^n p_ix_i$.
Donc
$\mathbb{E}(aX) = \displaystyle \sum_{i=1}^n p_i(ax_i)$
$\mathbb{E}(aX)= a \displaystyle \sum_{i=1}^n p_ix_i $
$\mathbb{E}(aX)= a \mathbb{E}(X)$.
Exemple :
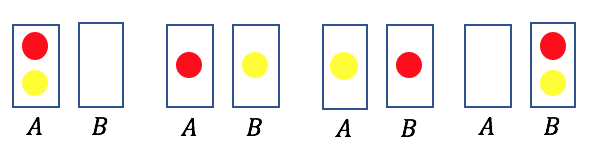
On place au hasard deux billes jaune et rouge dans deux boites $A$ et $B$.
Soit $X$ la variable aléatoire donnant le nombre de billes dans la boite $A$ et $Y$ le nombre de boites vides.
On représente les quatre situations possibles.
Dans la boite $A$, il peut y avoir $0$, $1$ ou $2$ billes. On peut alors compléter le tableau suivant.
| $x_i$ | 0 | 1 | 2 |
| $p_i$ | $\dfrac{1}{4}$ | $\dfrac{1}{2}$ | $\dfrac{1}{4}$ |
On peut alors calculer l’espérance de $X$ :
$\mathbb{E}(X) = 0 \times \dfrac{1}{4} + 1 \times \dfrac{1}{2} + 2 \times \dfrac{1}{4} $
$\mathbb{E}(X) = 1$.
Cela signifie qu’en moyenne il y a une bille dans la boite $A$.
Il peut y avoir une boite vide ou aucune des deux boites.
| $y_i$ | 0 | 1 |
| $q_i$ | $\dfrac{1}{2}$ | $\dfrac{1}{2}$ |
$\mathbb{E}(Y) = 0 \times \dfrac{1}{2} + 1 \times \dfrac{1}{2} $
$\mathbb{E}(Y) = \dfrac{1}{2} $.
D’après la propriété du cours, on a
$\mathbb{E}(X + Y) = \mathbb{E}(X) + \mathbb{E}(Y) $
$\mathbb{E}(X + Y) = 1 + \dfrac{1}{2} $
$\mathbb{E}(X + Y) = \dfrac{3}{2}$.