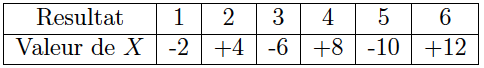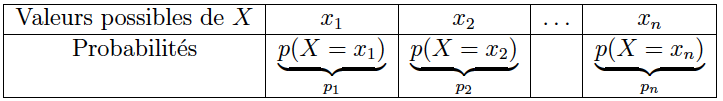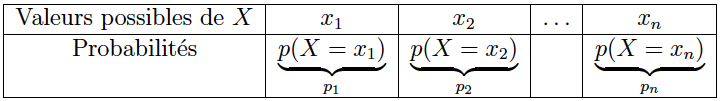Variable aléatoire et loi de probabilité
Variable aléatoire et loi de probabilité
I. Variable aléatoire
Définition de la variable aléatoire
Qu’est-ce qu’une variable aléatoire ?
Étant donnée une expérience aléatoire, on appelle variable aléatoire, toute grandeur numérique dont la valeur dépend de l’issue de l’expérience.
Exemple de variable aléatoire
On lance un dé à 6 faces.
Si le résultat est pair, le joueur gagne le double du résultat.
Si le résultat est impair, le joueur perd le double du résultat.
Soit $X$ la variable aléatoire mesurant le gain du joueur.
Voici les valeurs possibles de $X$ :
II. Loi de probabilité
Définition de la loi de probabilité
Qu’est-ce que la loi de probabilité ?
La loi de probabilité d’une variable aléatoire est l’ensemble des valeurs possibles de $X$ et les probabilités de chacune d’elles.
La somme des probabilités associées aux valeurs de $X$ est égale à 1.
$\displaystyle\sum_{i=1}^{n}p_i=1$
Erratum : Sur le tableau de l’exemple du 2) il est écrit \(-1\), il s’agit en fait de \(-2\).
Espérance de la variable aléatoire
Espérance de la variable aléatoire
Définition de l’espérance de la variable aléatoire
Qu’est-ce que l’espérance de la variable aléatoire ?
Soit $X$ une variable aléatoire et sa loi de probabilité :
On appelle espérance de la variable aléatoire $X$, le nombre $E(X)$ :
$E(X)=x_1 \times p_1+x_2 \times p_2+\ldots+x_n \times p_n$
$E(X)=\displaystyle\sum_{i=1}^{n}x_ip_i$
Exemple de l’espérance d’une variable aléatoire
Calculer l’espérance de $X$ :
$E(X)= -2 \times 0{,}2 + 3\times 0{,}3 + 5 \times 0{,}5 $
$E(X)=3$
Interprétation de l'espérance
Interprétation de l’espérance de la variable aléatoire
Qu’est-ce que l’interprétation de l’espérance de la variable aléatoire ?
L’espérance de $X$ représente la valeur moyenne de $X$ : c’est celle que l’on peut espérer obtenir en répétant un grand nombre de fois l’expérience.
Exemple
On lance une pièce truquée : la probabilité d’obtenir pile est de $0{,}6$.
- Si on obtient pile, on perd 1 euro.
- Si on obtient face, on gagne 2 euros.
Soit $X$ la variable aléatoire représentant le gain du joueur. Déterminer et interpréter son espérance.
Étape 1 : Loi de probabilité de $X$
Étape 2 : Calcul de l’espérance
$E(X)= -1 \times 0{,}6 + 2 \times 0{,}4 $
$E(X)= 0{,}2$
Étape 3 : Interprétation de l’espérance
En répétant un grand nombre de fois l’expérience, on peut espérer avoir un gain moyen de 0,2 soit 20 centimes d’euros par lancer.