Espace, droites et plans
Espace, droites et plans
Définitions
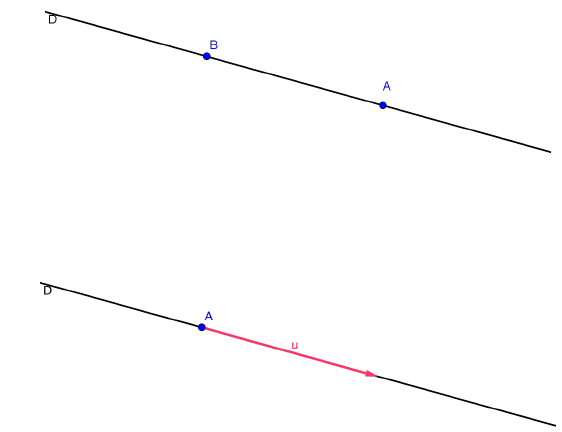
Une droite de l’espace peut être définie par :
- deux points ou
- un point et un vecteur directeur.
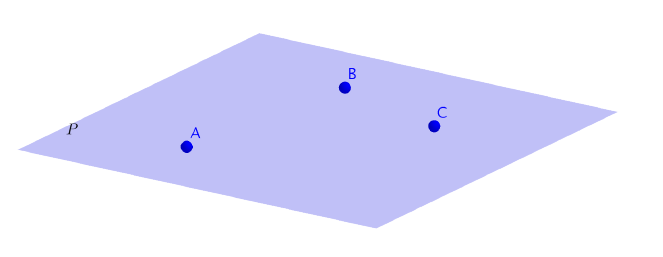
Un plan peut être défini par :
- trois points non alignés
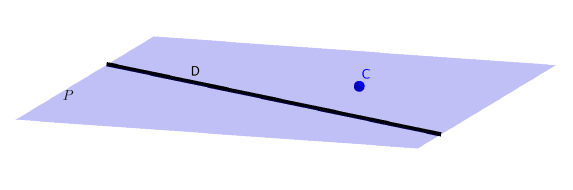
- Une droite et un point extérieur à la droite
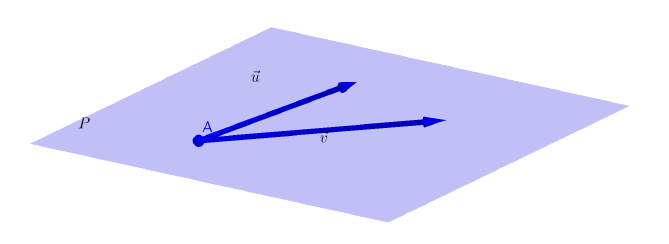
- Deux vecteurs non colinéaires et un point
Repères et coordonnées
Définition
On appelle repère de l’espace tout quadruplet $(O; \overrightarrow{i};\overrightarrow{j}; \overrightarrow{k}) $ constitué d’un point $O$ de l’espace et de trois vecteurs non coplanaires.
On note $(Ox)$ l’axe dirigé par $\overrightarrow{i}$, $(Oy)$ l’axe dirigé par $\overrightarrow{j}$ et $(Oz)$ l’axe dirigé par $\overrightarrow{k}$.
Lorsque les droites $(Ox)$, $(Oy)$ et $(Oz)$ sont perpendiculaires deux à deux, le repère est dit orthogonal.
Si de plus $||\overrightarrow{\imath}||=||\overrightarrow{\jmath}||=||\overrightarrow{k}||=1$, le repère est dit orthonormal.
Théorème
Soit $(O; \overrightarrow{i};\overrightarrow{j}; \overrightarrow{k}) $ un repère de l’espace.
Pour tout point $M$ de l’espace, il existe un unique triplet $(x ; y ; z)$ tels que
$\overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}$.
On dit alors que le point $M$ a pour coordonnées $(x ; y ; z)$ et on note $M(x;y;z)$.
Repère et coordonnées - Exercice 1
Dans le repère \((A; \overrightarrow{AB}; \overrightarrow{AD}; \overrightarrow{AE})\), donnons les coordonnées des sommets du cube.
- Étape 1 : Pour déterminer les coordonnées, on regarde les déplacements en abscisse, en ordonnée et en côte nécessaires pour se rendre de l’origine \(A\) au point.
Repère et coordonnées - Exercice 2
1) Calculons les coordonnées de \(I\), milieu de \([AG]\).
- Étape 1 : On définit les coordonnées de \(A\) et de \(G\).
- Étape 2 : Pour calculer les coordonnées du milieu d’un segment, on fait la demi-somme de chaque coordonnées.
Calculons \(AG\).
- Étape 3 : On utilise la formule du cours pour calculer la longueur d’un segment à partir des coordonnées de ses extrémités \(A\) et \(G\) :
\(AG = \sqrt{(x_G – x_A)^2 + (y_G – y_A)^2 + (z_G – z_A)^2}\).
Vecteurs colinéaires, applications
Soient \(A(1, 3, -2)\), \(B(4, 0, 2)\) et \(C(-2, y_C, z_C)\).
Déterminons \(y_C\) et \(z_C\) tels que \(A, B \text{ et } C\) soient alignés.
Objectif : Les points \(A, B \text{ et } C\) sont alignés si et seulement si les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{AC}\) sont colinéaires.
- Étape 1 : On détermine les valeurs des vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{AC}\).
- Étape 2 : On cherche \(k \in \mathbb{R^*}\) tel que \(\overrightarrow{AB} = k \overrightarrow{AC}\).
- Étape 3 : On exprime cette égalité sous forme d’un système que l’on peut résoudre.