Exponentielle - Croissances comparées
Croissances comparées
Pour $n$ appartenant à $\mathbb{N}$ :
1. $\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{e^x}{x} = +\infty$ ; $\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{e^x}{x^n}=+\infty$
2. $\displaystyle \lim \limits_{x \rightarrow -\infty} xe^x =0$ ; $\displaystyle \lim \limits_{x \rightarrow -\infty} x^ne^x =0$
A savoir aussi :
3. $ \displaystyle\lim_{x\to 0} \frac {e^x-1}{x}=1$
Exercice 1
Calculer : $\displaystyle \lim \limits_{x \rightarrow +\infty} x^3 -e^x$.
Corrigé
- étape 1 : On s’interroge sur la présence de formes indéterminées.
Il y en a une de la forme $\infty-\infty$. - étape 2 : On factorise par $e^x$ le numérateur et le dénominateur.
$\displaystyle \lim \limits_{x \rightarrow +\infty} e^x(\frac{x^3}{e^x}-1)$ - étape 3 : On utilise le théorème des croissances comparées.
On sait que $\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{e^x}{x^3} = +\infty$.
Donc $\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{x^3}{e^x} =\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{1}{\frac{e^x}{x^3}}= 0$.
Le terme entre parenthèses tend donc vers $-1$.
- étape 4 : Par produit de limites, on conclut donc :
$\displaystyle \lim \limits_{x \rightarrow +\infty} x^3 -e^x= -\infty$
Exercice 2
Calculer : $\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{e^x-x}{2e^x+3}$.
Corrigé
- étape 1 : On s’interroge sur la présence de formes indéterminées.
Il y en a au moins une au numérateur (de la forme $\infty-\infty$).
- étape 2 : On factorise par $e^x$ le numérateur et le dénominateur.
$\displaystyle\lim \limits_{x \rightarrow +\infty} \frac{e^x-x}{2e^x+3}=\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{e^x(1-\frac{x}{e^x})}{e^x(2+\frac{3}{e^x})} = \displaystyle \lim \limits_{x \rightarrow +\infty} \frac{1-\frac{x}{e^x}}{2+\frac{3}{e^x}}$
- étape 3 : On utilise le théorème des croissances comparées.
$\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{x}{e^x} = 0$ et $\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{3}{e^x}=0 $
- étape 4 : le numérateur tend vers $1$ et le dénominateur tend vers $2$. On conclut donc :
$\displaystyle \lim \limits_{x \rightarrow +\infty} \frac{e^x-x}{2e^x+3}= \frac{1}{2}$
Fonctions composées - exp(u(x))
Fonctions composées
Soit $u(x)$ une fonction continue et dérivable sur $\mathbb{R}$, la fonction $f(x)=e^{u(x)}$ a pour dérivée
$f'(x)=u'(x)e^{u(x)}$.
Exemple
Soit $g$ la fonction définie et dérivable sur $\mathbb{R}$ par :
$g(x)=e^{(-3x^2+x)}$.
Déterminons sa dérivée.
On pose : $u(x)= -3x^2+x$.
On a donc : $u'(x)=-6x+1$.
On a : $g'(x)= u'(x)e^{u(x)}$.
Soit : $g'(x)=(-6x+1)e^{(-3x^2+x)}$.
Autre exemple
Etudier les variations de la fonction $f(x)$= $\displaystyle \frac{3e^x}{e^{2x}+1}$.
étape 1 : On cherche toujours l’ensemble de définition d’une fonction.
$Df= \mathbb{R} $ car $e^{2x}$ ne peut être égal à $-1$, c’est toujours positif.
étape 2 : On cherche les limites aux bornes de l’ensemble de définition : en $+\infty$ et en $-\infty$.
On factorise par $e^x$ et on simplifie pour lever l’indétermination.
$\displaystyle \lim \limits_{x \rightarrow +\infty}f(x)=\lim \limits_{x \rightarrow +\infty}\frac{e^x\times 3}{e^{x}(e^{x}+\displaystyle\frac{1}{e^{x}})}=\lim \limits_{x \rightarrow +\infty}\frac{3}{e^{x}+\displaystyle\frac{1}{e^{x}}}=0$ car
$\displaystyle \lim \limits_{x \rightarrow +\infty}e^x+\frac{1}{e^x}=+\infty$
$\displaystyle \lim \limits_{x \rightarrow -\infty}f(x)=\lim \limits_{x \rightarrow -\infty}\frac{3}{e^{x}+\displaystyle\frac{1}{e^{x}}}=0$ car
$\displaystyle \lim \limits_{x \rightarrow -\infty}e^x+\frac{1}{e^x}=+\infty$
étape 3 : On dérive $f$ comme quotient de fonctions dérivables sur $\mathbb{R}$.
On utilise la formule suivante :
$\displaystyle (\frac{u}{v})’=\frac{u’v-uv’}{v^2}$.
$\displaystyle u(x)=3e^x, u'(x)=3e^x \hspace{0.2cm} \text{et} \hspace{0.2cm} v(x)=e^{2x}+1, v'(x)= 2e^{2x}$
$\displaystyle f'(x)= \frac{3e^x (e^{2x}+1)-3e^x (2e^{2x})}{(e^{2x}+1)^2}$
$\displaystyle f'(x)= \frac{3e^x (1-e^{2x})}{(e^{2x}+1)^2}$
On remarque que $(1-e^{2x})$ est une égalité remarquable égale à $(1-e^x)(1+e^x)$.
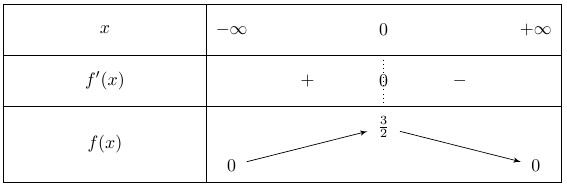
Le signe de $f'(x)$ est du signe de $(1-e^x)(1+e^x)$ donc de $(1-e^x)$.
On a :
$(1-e^x)\geq 0 \iff 1\geq e^x \iff 0\geq x$
On en déduit le tableau de variations :
Fonctions composées - exp(u(x)) - Exercice
Exercice
Étudions la fonction \(f(x) = \large\frac{3e^x}{e^{2x} + 1}\).
Étape 1 : On cherche toujours l’ensemble de définition d’une fonction.
Étape 2 : On cherche les limites aux bornes de l’intervalle : en \(+\infty\) et en \(-\infty\).
Étape 3 : On factorise pour lever l’indétermination.
Étape 4 : On utilise ici que \(\displaystyle\lim_{x \to -\infty} e^x = 0\).
Étape 5 : On utilise la formule \((\frac{u}{v})’ =\large \frac{u’v – uv’}{v^2}\) pour étudier les variations.