Nuage de points, point moyen
Nuage de points – Point moyen
Définition
L’ensemble des points $(x_i; y_i)$ dans un repère est appelé nuage de points associé à la série statistique. Une série statistique peut également être représentée sous forme d’un tableau.
Le point moyen, qui correspond à la moyenne de la série, a pour coordonnées $G(\overline{x}, \overline{y})$ avec :
$\overline{x} = \dfrac{x_1+x_2+…+x_n}{n}$ et
$\overline{y} = \dfrac{y_1+y_2+…+y_n}{n}$
Exemple :
On étudie les salaires annuels des attaquants de L1 de football et le nombre de buts marqués dans une saison.
On représente sous forme de tableau les résultats de cette étude, en indiquant sur la première ligne la première variable “Nombre de buts” et sur la seconde ligne la variable “Salaire annuel en millions d’euros”
| Nombre de buts $(x_i)$ | 2 | 8 | 11 | 16 | 20 |
| Salaire annuel en millions d’euros ($y_i$) | 3,5 | 4,7 | 5,2 | 7,6 | 9,5 |
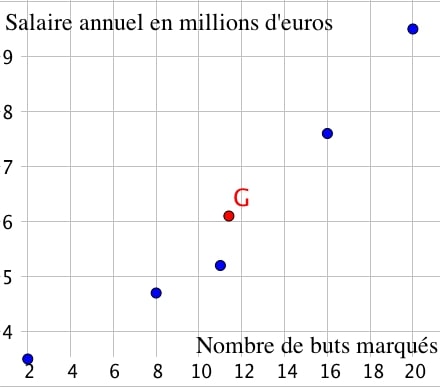
On commence par tracer le nuage de points de la série statistique. L’abscisse des points correspond au nombre de but et l’ordonnée au salaire annuel.
On fera attention à ne pas relier les différents points du graphique car il s’agit d’un nuage de points et non d’une droite.
On détermine ensuite les coordonnées du points moyen :
$\overline{x} = \dfrac{2+8+…+20}{5}=11.4$ et
$\overline{y} = \dfrac{3.5+4.7+…+9.5}{5}=6.1$
Ainsi, $G(11.4; 6.1)$