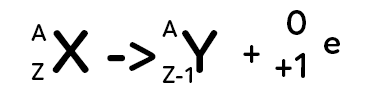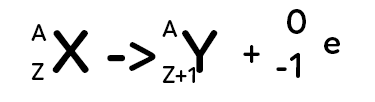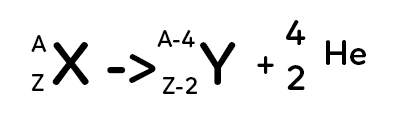Introduction à la physique nucléaire
La physique nucléaire est la physique du noyau de l’atome. On ne va vraiment s’intéresser qu’au noyau de l’atome et ne pas s’occuper des électrons qui sont en mouvements autour du noyau de l’atome.
Rappel sur la composition du noyau de l’atome
\({_Z^A}X\)
\(A\) : nombre de nucléons (protons et neutrons)
\(Z\) : nombre de protons
\(N = A-Z\) : nombre de neutrons
\(X\) : le symbole de l’atome
Isotopes
En physique nucléaire, on parle souvent des isotopes parce que les isotopes n’ont pas tout à fait les mêmes propriétés nucléaires. Deux noyaux d’atomes isotopes sont deux noyaux d’atomes qui ont le même nombre de protons, mais un nombre de neutrons différents.
\({_1^1}H\) \( \ \ {_1^2}H\) \( \ \ {_1^3}H\)
Ci-dessus sont représentées les isotopes de l’hydrogène. On remarque qu’en bas, le nombre de protons est le même, mais qu’en haut, c’est un chiffre différent.
Écriture d’une réaction nucléaire
En physique nucléaire, on a des réactions nucléaires. Dans ces réactions nucléaires, les noyaux d’atomes sont modifiés. On écrit la réaction nucléaire de la façon suivante :
\({_{Z_1}^{A_1}}X_1 + {_{Z_2}^{A_2}}X_2 \rightarrow {_{Z_3}^{A_3}}X_3 + {_{Z_4}^{A_4}}X_4\)
Elle ressemble à l’écriture de l’équation d’une réaction chimique. On met les noyaux ou particules qui sont présents initialement avec leur symbole, on met une flèche et on termine avec les noyaux ou particules présents à la fin de la réaction nucléaire.
Pour une réaction nucléaire, on a trois conservations :
La conservation de la charge : les particules chargées dans les noyaux sont les protons, donc si la charge se conserve lors d’une réaction nucléaire, cela veut dire qu’on a la relation suivante : $Z_1+Z_2 = Z_3+Z_4.$ Il faudra toujours vérifier dans une réaction nucléaire si la charge est bien conservée.
La conservation du nombre de nucléons : dans le cas de l’écriture globale de la réaction nucléaire, cela implique que : $A_1+A_2 = A_3+A_4.$ Il faudra ainsi vérifier qu’on a bien une conservation du nombre de nucléons quand on a une équation de réaction nucléaire.
La conservation de l’énergie.
Remarque
Certaines particules ne sont pas des noyaux d’atomes mais ont une représentation symbolique que l’on utilise dans l’écriture des réactions nucléaires.
Une particule que l’on connaît bien est l’électron. Son symbole est \({_{-1}^0}e\). $0$ car il n’y a pas de nucléons, $-1$ car il a une charge opposée à celle du proton.
Une autre de ces particules est le positon ou positron. C’est l’antiparticule de l’électron. Il a le même symbole mais il a une charge opposée à celui de l’électron donc $+1$ en bas : \({_{+1}^0}e\).
Enfin, le neutron qui a pour symbole \({_0^1}n\). $1$ car il y a un neutron donc un nucléon, et $0$ car, par définition, le neutron est neutre donc il a une charge nulle.
La radioactivité
La radioactivité
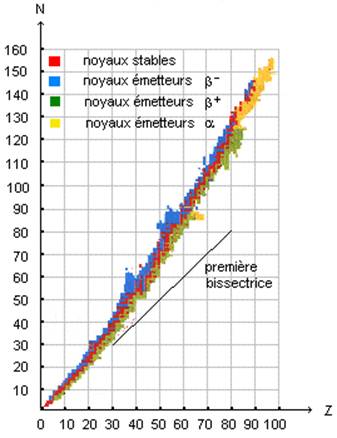
La radioactivité est l’ensemble des transformations spontanées des noyaux d’atomes instables. On parle de transformations spontanées car elles ne nécessitent pas d’apport d’énergie de l’extérieur. Ce ne sera pas le cas pour des réactions de fusion et de fission. Ces noyaux d’atomes instables se transforment en noyaux d’atomes un peu plus stables, le tout en émettant des rayonnements, d’où le nom de radioactivité. Pour expliquer l’instabilité des noyaux d’atomes, on utilise le diagramme de Ségré.
Sur le diagramme de Ségré, on représente tous les noyaux d’atomes connus à ce jour en fonction de leur nombre de neutrons, en ordonnées, et du nombre de protons, en abscisses. On observe que les noyaux d’atomes stables sont approximativement situés sur la droite $N=Z$. Cela signifie que globalement, lorsqu’un noyau d’atome a autant de neutrons que de protons, il risque d’être stable. Lorsqu’un noyau d’atome s’éloigne de cette droite $N=Z, $ on a de l’instabilité et de la radioactivité. Les trois causes d’instabilité des noyaux d’atome sont :
– L’excès de protons par rapport aux neutrons.
– L’excès de neutrons par rapport aux protons.
– L’excès de neutrons et de protons, pour les noyaux d’atomes lourds.
Excès de protons par rapport aux neutrons
Le noyau d’atome représenté par $^A_ZX$ (noyau père) se transforme en un autre noyau d’atome (noyau fils) qui aura un symbole différent. En effet, on constate qu’on est passé de $Z$ à $Z-1$ pour les protons du noyau donc ce n’est plus le même élément qui est concerné. Il y a un proton qui va se transformer en un neutron et cela provoque l’émission d’une particule appelée positon. On peut vérifier qu’il y a bien la conservation du nombre de nucléons puisqu’on a $A = A+0$ et $Z = Z-1+1.$ On parle de rayonnement $β^+$ car un positon est émis.
Excès de neutrons par rapport aux protons
Le noyau père est instable. Le neutron se transforme en proton dans le noyau de l’atome. Cela va donner un noyau fils qui a un autre symbole puisque le numéro $Z$ va se changer en $Z+1.$ Lorsqu’il y a cette transformation, cela émet un électron. Attention, cet électron ne fait pas partie du nuage électronique mais il va être, en quelque sorte, éjecté du noyau. C’est la radioactivité $β^-$ car l’électron est chargé négativement.
Excès de neutrons et de protons, pour les noyaux d’atomes lourds
Le noyau père se transforme en noyau fils en éjectant deux protons et deux neutrons. Deux protons et deux neutrons correspondent au noyau d’hélium. On parle ici de radioactivité $\alpha.$ Le noyau d’hélium est aussi appelé particule $\alpha.$
Ces trois transformations nucléaires, qu’on appelle aussi désintégrations radioactives, s’accompagnent de l’émission de rayonnement $γ.$ C’est un rayonnement électromagnétique de haute énergie qui provient du fait que ces noyaux fils sont dans un état excité, ont un surplus d’énergie. Cela va provoquer l’émission de ces rayonnements.
Radioactivité naturelle et artificielle
La radioactivité est avant tout un phénomène naturel, puisqu’on a des éléments radioactifs dans la nature. Un exemple d’application de cette radioactivité naturelle est la datation, par exemple, des momies au carbone 14. Le carbone 14 est un élément radioactif.
La radioactivité peut être aussi artificielle, ce sont les isotopes radioactifs qui sont fabriqués par l’Homme. On peut avoir différentes applications, par exemple dans le domaine médical avec ce qu’on appelle l’imagerie TEP (Tomographie par Emission de Positons). C’est la particule de la radioactivité $β^+.$ On injecte des isotopes radioactifs.
Activité radioactive
Activité radioactive
La radioactivité est l’ensemble des transformations spontanées des noyaux d’atomes instables qui s’accompagnent de l’émission de rayonnements.
Comment mesurer cette radioactivité ?
Pour mesurer la radioactivité, on dispose de compteurs qui comptent le nombre de désintégrations. On définit l’activité radioactive comme le nombre de désintégrations par seconde. Ce nombre est un nombre moyen donc le calcul est le nombre moyen de désintégrations par seconde.
Par définition, on calcule l’activité grâce à la formule suivante : $A = \dfrac{nombre \ moyen \ de \ désintégrations}{Δt}$
Avec $Δt$ la durée de comptage exprimée en secondes et $A$ l’activité exprimée en becquerels (Bq) en hommage au scientifique Henri Becquerel qui a découvert la radioactivité.
Un becquerel est égal à une désintégration par seconde.
Calculer une activité à partir de résultats de compteur
Exemple
On a une source radioactive et on a fait des comptages sur une durée de cinq secondes. On trouve différents résultats sur cinq secondes :
296 – 298 – 302 – 308 – 298 – 300 – 297
On se rend compte que le nombre de désintégrations n’est pas tout à fait le même mais tourne autour du même résultat. Donc, pour calculer l’activité radioactive, il suffit de faire la moyenne sur toutes ces valeurs (les additionner et diviser par 7). Si on fait le calcul, on trouve environ 300 désintégrations en moyenne et ensuite on divise par la durée de comptage : 5 secondes.
On a alors : $A = \dfrac{300}{5} = 60 \ Bq$.
L’activité dépend de nombreux paramètres
Elle dépend :
– De la nature de la source.
– Du temps. En effet, plus le temps passe, moins une source est radioactive. Donc la radioactivité va avoir tendance à diminuer en fonction du temps.
– De la masse de l’échantillon.
– De la distance à la source. Plus on s’éloigne et plus l’activité va diminuer.
Elle dépend également d’autres paramètres, mais ce sont les principaux à retenir pour l’activité radioactive.
Ordres de grandeur d’activité pour quelques sources radioactives
Pour comparer justement l’activité puisqu’elle dépend de la masse, on va comparer l’activité par kilogramme, sinon cela n’a pas de sens.
L’Homme est radioactif puisqu’il possède des éléments radioactifs comme le potassium 40 ou le carbone 14. Il a une activité moyenne de 100 Bq/kg.
L’uranium utilisé dans les centrales nucléaires, a une activité moyenne de 108 Bq/kg. On voit donc le rapport d’activité.
Le lait en poudre a une activité moyenne de 250 Bq/kg. Pour les aliments, en général, on est entre 100 et 500 Bq/kg.
Loi de décroissance radioactive
Loi de décroissance radioactive
Un atome radioactif est un atome qui va se transformer spontanément en un autre atome en émettant des rayonnements.
I. Evolution d’un échantillon dans le temps
On considère un échantillon qui a un nombre de noyaux d’atomes radioactifs $N_0$. Voyons comment évolue cet échantillon dans le temps, c’est-à-dire, comment évolue le nombre de noyaux d’atomes radioactifs dans le temps ?
On a une formule qui est une équation différentielle du premier ordre et qui exprime la variation du nombre d’atomes radioactifs en fonction du temps.
On a alors : $\dfrac{dN(t)}{dt} = -\lambda N(t)$
$\lambda$ est une constante radioactive qui dépend du noyau d’atome considéré : Carbone 14, Uranium 238, etc.
Cette équation différentielle du premier ordre a une solution de la forme : $N(t) = Ke^{-\lambda t}$.
On doit connaître le type de solution associé à l’équation différentielle par cœur.
La constante $K$ est toujours déterminée par les conditions initiales. Cela revient à dire qu’à l’état initial, quand $t = 0$, on a : $N(0) = Ke^{-\lambda \times 0} = K = N_0$.
On trouve la loi de décroissance radioactive : $N(t) = N_0 e^{-\lambda t}$
avec $N_0$ le nombre de noyaux initial,
$\lambda$ la constante radioactive qui dépend du noyau,
et $t$ l’instant dans lequel on étudie le phénomène.
II. Expression graphique
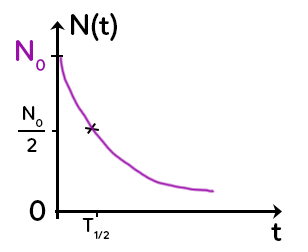
Cette loi est bien connue car elle s’exprime graphiquement sous la forme d’une exponentielle décroissante avec le nombre de noyaux radioactifs en fonction du temps.
À partir de cette courbe, on peut déterminer la demi-vie, qui caractérise l’atome radioactif, et aussi l’expression de la demi-vie en fonction de la constante radioactive. Le temps de demi-vie est le temps qu’il faut pour que la moitié des atomes radioactifs initialement présents soient désintégrés.
Graphiquement, pour trouver le temps de demi-vie, on prend $N_0$, on divise par deux et on le reporte sur l’axe des ordonnées. On lit ensuite l’abscisse correspondante pour avoir le temps de demi-vie $t_{1/2}.$
Pour calculer le temps de demi-vie, on utilise la loi de décroissance radioactive et on dit qu’au temps de demi-vie : $N(t_{1/2}) = \dfrac{N_0}{2} N_0e^{-\lambda t_{1/2}}$
On peut simplifier les $N_0$ et on applique le logarithme népérien pour enlever l’exponentielle : $ln(\dfrac{1}{2}) = ln(e^{-\lambda t_{1/2}})$
Donc : $ln2 = -\lambda t_{1/2}$ et $t_{1/2} = \dfrac{ln2}{\lambda}$
Cela permet de connaître le temps de demi-vie d’un atome radioactif en connaissant sa constante radioactive.