Image d'un nombre par une fonction
Image d’un nombre par une fonction
Notion intuitive d’image
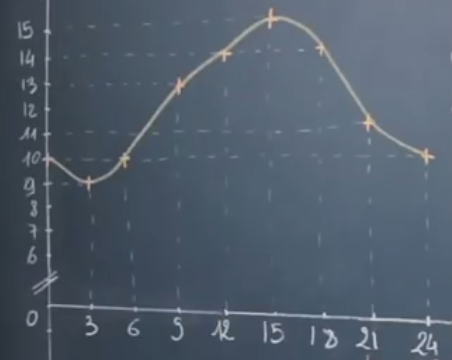
Considérons la courbe de température suivante :
L‘ensemble de définition de la fonction est $[0, 24]$, c’est à dire que l’étude se fait sur une journée complète à partir de minuit.
L’ordonnée est la température, il s’agit donc de la représentation graphique de la température en fonction du temps.
Ainsi, le temps est sur l’axe des abscisses.
Question : quelle température faisait-il à 3h du matin ?
On lit graphiquement que la température à 3h du matin est 9°C.
Ainsi, on dira que l’image de 3 par la fonction $f$ vaut 9 : il n’y a plus d’unité. On notera aussi $f(3) = 9$.
Définition
Soit $f$ une fonction et $a$ et $b$ deux réels vérifiants $f(a)=b$.
On dit que $b$ est l’image de $a$ par $f$.
Ou encore : l’image de $a$ par $f$ vaut $b$.
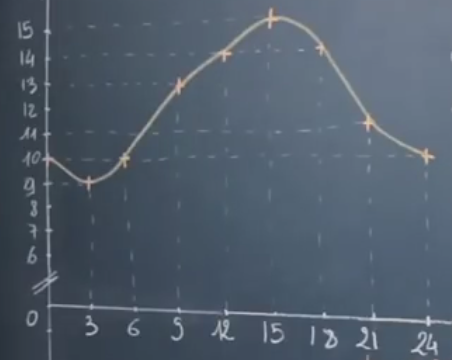
Autre exemple :
Pour trouver l’image de 15, on se place sur l’axe des abscisses à $t = 15$ puis on trace la droite perpendiculaire à cet axe et on regarde l’ordonnée du point d’intersection entre cette droite et la courbe de $f$ :
On lit $f(15) = 15$.
Antécédent d'un nombre par une fonction
Antécédent d’un nombre par une fonction
Définition
Soit $f$ une fonction et deux réels $a$ et $b$ vérifiant $f(a)=b$
On dit que $b$ est l’image de $a$ par $f$. (c’est une valeur unique)
On dit que $a$ est un antécédent par $f$ de $b$. (il peut y en avoir plusieurs)
Exemples
Cherchons le ou les antécédents, s’ils existent de $14$
Cela revient à chercher l’heure à laquelle la température était de 14°C.
Pour ce faire, on se place sur l’axe des ordonnées (l’axe des températures ici) et on trace la droite perpendiculaire à cet axe puis on regarde les points d’intersection entre la droite et la courbe de température et finalement, on lit leur abscisse.
Ici, il y a deux points d’intersections pour lesquels la température est de 14°C et donc deux heures différentes : 12h et 18h.
Il se peut que dans certains cas il n’y ait aucune solution.
Mathématiquement, le fait qu’il ait fait 14°C à 12h et 18h se traduit par :
Les antécédents de 14 par la fonction $f$ sont 12 et 18.
Ou encore : les solutions de l’équation $f(t) = 14$ sont $S = \{12; 18\}$.
Considérons l’équation $f(t) = 10$ : on cherche donc les antécédents de 10 par $f$.
Les solutions sont donc $S = \{0; 6; 24\}$.
Considérons l’équation $f(t) = 16$ : on cherche donc les antécédents de 16 par $f$.
La température de 16°C n’étant jamais atteinte, cette équation n’admet pas de solution :
$S = \varnothing$.
Fonction linéaire, fonction affine
Fonction linéaire, fonction affine
Fonctions linéaires
Une fonction linéaire est un procédé qui à un nombre $x$ associe un nombre $f(x)$ de la forme $f(x) = ax$ où $a$, le coefficient directeur, est un nombre donné et on la note $x \xrightarrow{f} f(x) = ax$.
Une fonction linéaire aura pour représentation graphique une droite passant toujours par l’origine du repère, c’est à dire le point de coordonnées $(0; 0)$.
Selon la valeur de $a$, l’inclinaison de la droite sera différente : plus $a$ est grand (et positif), plus la droite monte, plus $a$ est petit et positif, moins la droite monte. Si $a$ est négatif, la droite descend.
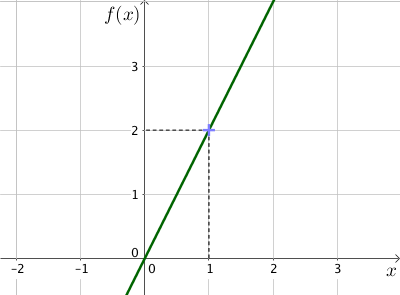
Sur le graphique, la fonction $f$ associe au nombre 1 le nombre 2.
Ainsi $f(1) = 2$.
Or la forme générale de $f$ est $f(x) = a \times x$ donc $f(1) = a \times 1 = a$ et $f(1) = 2$ donc $a = 2$.
Ainsi ce graphique est le représentation graphique de la fonction $f(x) = 2x$.
Fonctions affines
Une fonction affine est de la forme $x \xrightarrow{f} f(x) = ax + b$ où $a$, le coefficient directeur, et $b$, l’ordonnée à l’origine, sont des nombres donnés.
$b$ s’appelle l‘ordonnée à l’origine car la représentation graphique des fonction affines est une droite qui coupe l’axe des ordonnées au point $b$.
La valeur de $a$ donne l’inclinaison de la droite. Plus $a$ est grand et positif, plus la droite monte; plus $a$ est petit, plus la droite descend.
Enfin, les fonctions linéaires sont un cas particulier des fonctions affines, avec $b = 0$.
Déterminer une fonction affine connaissant 2 points - Le rappel de cours
Déterminer une fonction affine connaissant 2 points
Méthode :
Une fonction affine est de la forme $f(x) = ax + b$, où $a$ est le coefficient directeur et $b$ l’ordonnée à l’origine.
Il s’agit de déterminer les valeurs de $a$ et de $b$ connaissant les coordonnées de deux points appartenant à la représentation graphique de $f$.
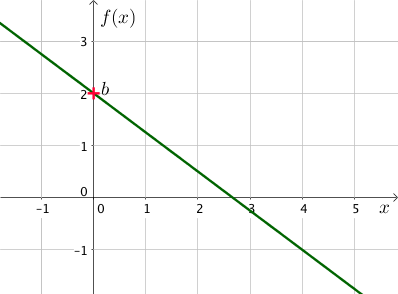
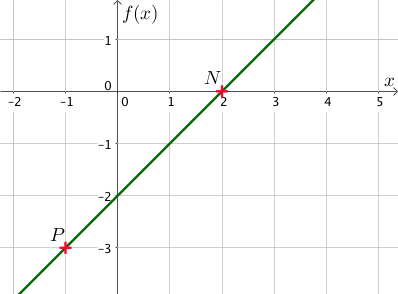
La représentation graphique ci-dessous n’est point utile mais permet tout de même de visualiser la fonction $f$.
Les points connus sont $N(2; 0)$ et $P(-1; -3)$.
Si un point appartient à la courbe représentative de la fonction $f$, alors ses coordonnées vérifient l’équation de $f$, sachant que $x$ correspond à l’abscisse du point et $f(x)$ à son ordonnée.
Ainsi, comme $N$ appartient à la droite, on peut alors écrire : $a \times 2 + b = 0$.
De même, $P$ appartient à la droite, donc $a \times (-1) + b = -3$.
Ces deux équations à deux inconnues permettent donc d’écrire un système d’équation qu’il faut résoudre :
$\left \{ \begin{array}{c} 2a + b = 0 \\ -a + b = -3 \\ \end{array} \right.$
Il suffit ensuite d’isoler $b$ :
$\left \{ \begin{array}{c} b = -2a \\ b = -3 + a \\ \end{array} \right.$
Ainsi, $-2a = -3 + a$ : $a$ est alors l’unique inconnue. On résout alors cette équation $-3a = -3$ donc $a = 1$.
Enfin, pour déterminer $b$, il suffit de remplacer dans une des deux équations $a$ par sa valeur : $b = -2\times 1 = -2$.
La fonction $f$ s’écrit donc
$f(x) = x – 2$
Il est alors possible de vérifier ce résultat à l’aide du graphique.
Le coefficient directeur est 1. L’ordonnée à l’origine est -2.