Inéquation du 1er degré
Inéquation du 1er degré
I) Résolution d’une inéquation du 1er degré
Résoudre une inéquation revient à trouver les valeurs de $x$ pour lesquelles l’inégalité est vérifiée.
Règle 1 :
On ne change pas le sens de l’inégalité en additionnant ou en soustrayant un même nombre à ses deux membres.
Règle 2:
On ne change pas le sens de l’inégalité en multipliant ou en divisant par un même nombre strictement positif ses deux membres.
Règle 3:
On change le sens de l’inégalité en multipliant ou en divisant par un même nombre strictement négatif ses deux membres.
Exemple :
On souhaite résoudre l’inéquation $7x – 3 > 2x – 1$
On souhaite regrouper les $x$ du même côté de l’inégalité.
Pour cela, on soustrait $2x$ des deux côtés de l’inégalité.
$7x – 2x – 3> 2x – 2x – 1$
$5x – 3>- 1$
On regroupe ensuite les nombres de l’autre côté de l’inégalité.
$5x -3 + 3 > – 1 + 3$
$5x > 2$.
Pour isoler $x$, on divise enfin par $5$. On ne change pas le sens de l’inégalité car $5 > 0$.
$\dfrac{5x}{5} > \dfrac{2}{5}$
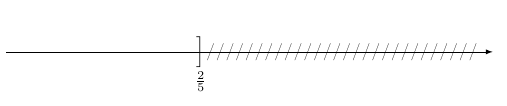
$x > \dfrac{2}{5}$
Les solutions de cette inéquations sont les nombres strictement supérieurs à $\dfrac{2}{5}$.
On peut représenter l’ensemble de ces solutions par une droite graduée. On indique par un crochet ouvert que l’on ne veut pas le nombre $\dfrac{2}{5}$ car il s’agit d’une inégalité stricte.
II) Résolution d’un problème
La méthode utilisée ici est la même que pour la résolution d’un problème faisant intervenir une équation du premier degré : il y a quatre étapes.
On considère le problème suivant pour appliquer la méthode.
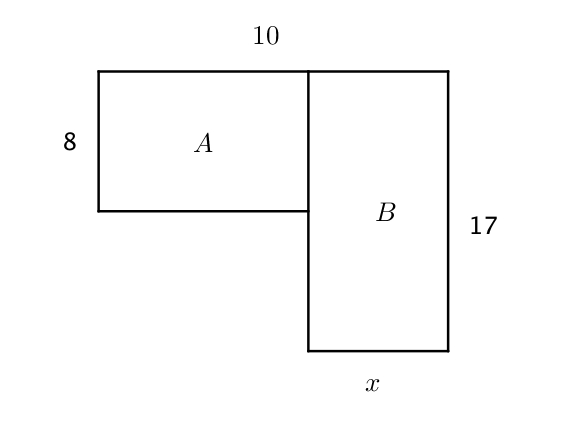
Pour quelles valeurs de $x$ le périmètre du rectangle $A$ est supérieur à celui de $B$ ?
1) Recherche de l’inconnue
L’inconnue est généralement donnée dans l’énoncé du problème.
Ici, l’inconnue est $x$, la largueur du rectangle $B$.
2) Mise du problème en équation
L’énoncé évoque les périmètres des rectangles $A$ et $B$.
Il s’agit donc d’abord de calculer ces périmètre.
Le périmètre du rectangle $A$ vaut $2\times (8 + (10 – x)) = 36 – 2x$.
Le périmètre du rectangle $B$ vaut $2\times (-x + 18) = 2x + 34$.
Or, on cherche les valeurs de $x$ pour lesquelles le périmètre de $A$ est supérieur à celui de $B$, c’est à dire on veut résoudre l’inéquation
$36 – 2x > 2x + 34$.
3) Résolution de l’inéquation
On résout l’inéquation $36 – 2x > 2x + 34$
$36 – 2x + 2x > 2x + 2x + 34$
$36 > 4x + 34$
$36 – 34 > 4x + 34 – 34$
$2 > 4x$
$\dfrac{2}{4}> \dfrac{4x}{4}$, on ne change pas le sens de l’inégalité car $4>0$.
Ainsi, $0,5 > x$.
Les solutions sont donc les nombres strictement inférieurs à $0,5$.