Loi d'Ohm
Loi d’Ohm
I. La résistance électrique
Qu’est-ce que la résistance électrique ? Elle traduit l’aptitude d’un appareil électrique à s’opposer au passage du courant. Son symbole est $R$ (comme résistance), son unité c’est l’ohm qui se note $Ω.$ La résistance électrique apparaît justement dans la loi d’Ohm.
II. La loi d’Ohm
La loi d’Ohm concerne les appareils électriques ayant une résistance $R$ et parcourus d’un courant $i.$ Ils ont alors une tension $U$ telle que :
$U = R\times i,$ avec $U$ en volts (V), $R$ en ohms ($Ω$) et $i$ en ampères (A).
Cela signifie que la tension $U$ et le courant $i$ qui traversent un appareil électrique sont deux grandeurs proportionnelles. Graphiquement, cela se traduit par une droite qui passe par l’origine :
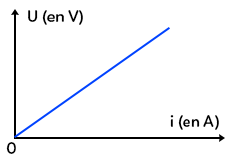
On trace la tension (en V) en ordonnée et l’intensité (en A) en abscisse. On a bien une droite qui passe par l’origine. Le coefficient directeur de cette droite est $R = \dfrac{U}{i}$, R étant la résistance électrique. On a des relations équivalentes :
$U = R\times i$ ou $R = \dfrac{U}{i}$ ou $i = \dfrac{U}{R}$
Ces trois relations permettent de trouver soit $U,$ soit $R,$ soit $i,$ en connaissant les autres grandeurs dans les exercices.
III. L’effet Joule
Il concerne les appareils qui obéissent, suivent, la loi d’Ohm. Pour rappel, la puissance électrique vaut $P = U\times i$, avec $P$ en watts (W), $U$ en volts (V) et $i$ en ampères (A).
La relation générale entre puissance et énergie est égale à $E = P\times t,$ avec $E$ en joules (J), $P$ en watts (W) et $t$ en secondes (s). Il faut retenir ces unités qui sont cohérentes entre elles.
Pour un appareil qui obéit à la loi d’Ohm, on a $U = R\times i$. Si on juxtapose toutes ces formules, on a donc : $P = R\times i \times i = R\times i^2$.
Comme l’énergie est le produit de la puissance par le temps, on a donc : $E = Ri^2t$.
Cette énergie est appelée énergie dissipée par effet Joule. C’est en fait de la chaleur qui va être émise par l’appareil électrique.


