ET - OU
ET – OU
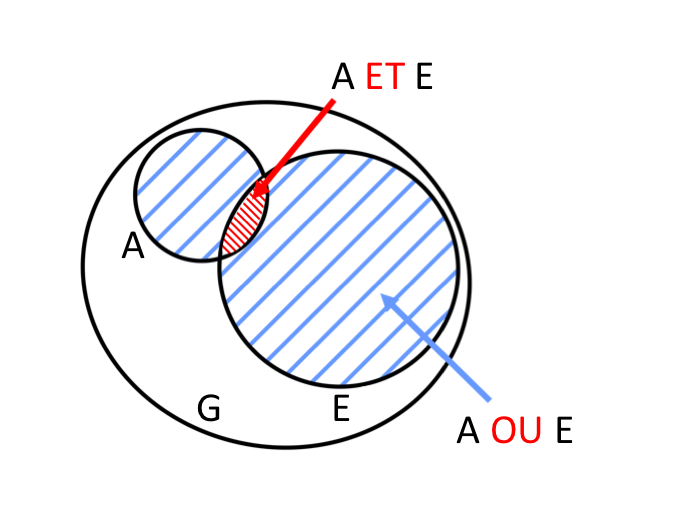
On considère un groupe de personnes, en différenciant les personnes qui satisfont le critère $A : \text{“Parler anglais”}$ ou $B : \text{“Parler espagnol”}$.
La notion de “ET”, qui a des liens avec l’outil mathématique Intersection, traduit le fait d’appartenir aux deux catégories à la fois :
$A$ ET $ B$ signifie donc parler les deux langues.
La notion de $A$ OU $E$ signifie parler l’une au l’autre langue, ou les deux.
Le “OU” mathématique se différencie du “OU” français, car en mathématiques, le “OU” n’est pas exclusif : on peut donc appartenir aux deux catégories.
En français, on demandera par exemple si une personne souhaite du thé ou du café. On sous-entend ici que la personne ne prendra par les deux, cela revient à lui demander si elle veut du thé ou bien du café.
Réciproque et contraposée
Réciproque et contraposée
Définition : propriété mathématique
Une propriété en mathématiques se présente sous la forme “SI ….. ALORS ….”.
Par exemple, si $ABCD$ est un carré, alors il a 4 angles droits.
“$ABCD$ est un carré” est la condition, notée $P$.
“il a 4 angles droits” est la conclusion, notée $Q$.
On notera alors $P \Rightarrow Q$.
Il s’agit d’une notation qui n’est pas exigible qui signifie que $P$ implique $Q$, ou encore “si $P$ alors $Q$”.
Définition de la réciproque d’une propriété
On obtient la réciproque d’une propriété en inversant la condition et la conclusion.
Une réciproque peut être vraie ou fausse.
Exemple
En reprenant l’exemple précédent, la réciproque est :
Si un quadrilatère a 4 angles droits, alors c’est un carré.
On remarquera que l’on n’a pas uniquement réécrit l’énoncé inverse, mais que l’on a précisé dans la condition le sujet de la réciproque.
Cette réciproque est fausse. En effet, un rectangle a 4 angles droits mais n’est pas un carré.
Remarques
Les réciproques du théorème de Thalès et de Pythagore sont vraies.
On notera alors $Q \Rightarrow P$ si la réciproque est vraie.
Définition de la contraposée d’une propriété :
Elle se construit en prenant la négation de la conclusion puis la négation de la condition.
Une contraposée est toujours vraie.
Exemple
La contraposée de la première propriété est : si un quadrilatère n’a pas 4 angles droits, alors ce n’est pas un carré.
On notera alors $\text{non } Q \Rightarrow \text{non } P$.
Condition nécessaire, condition suffisante
Condition nécessaire, condition suffisante
Condition nécessaire
Il s’agit d’une notion difficile. On considère un exemple pour la présenter.
“Si $ABCD$ est un carré, Alors il a 4 angles droits”
Notons : $P$ : “$ABCD$ est un carré” et $Q$ : “il a 4 angles droits”.
On peu ainsi noter
$P \Rightarrow Q$, qui signifie que $P$ implique $Q$ ou encore si $P$ alors $Q$.
On cherche une des conditions pour que $P$ soit vraie, c’est à dire, pour que $ABCD$ soit un carré : il faut absolument que $Q$ soit vraie aussi, c’est à dire que $ABCD$ ait 4 angles droits.
En effet, si $ABCD$ n’a pas 4 angles droits, d’après la contraposée de la propriété, il ne peut être un carré.
Ainsi, pour que $P$ soit vraie, il faut que $Q$ le soit.
$Q$ est donc une condition nécessaire à $P$.
Condition suffisante
On peut également chercher une condition pour que $Q$ soit vraie, c’est à dire que $ABCD$ ait 4 angles droits.
Pour cela, $ABCD$ peut être un carré, c’est à dire qu’il suffit que $ABCD$ soit un carré.
$P$ est donc une condition suffisante à $Q$.
Enfin, pour que $ABCD$ ait 4 angles droits, il ne faut pas que $ABCD$ soit uniquement un carré, cela signifie que si $ABCD$ est un rectangle, alors il possède aussi 4 angles droits.
En conclusion, une condition nécessaire s’exprime avec “il faut que”, alors qu’une condition nécessaire s’exprime avec “il suffit que”.
Contre-exemple
Contre-exemple
Définition
Un contre-exemple est un exemple qui contredit une affirmation ou une proposition
Remarques
Un contre exemple sert à prouver qu’une proposition est fausse.
Pour prouver qu’une proposition est vraie, donner un exemple ne permet pas de démontrer la proposition.
En revanche, il suffit qu’une proposition soit fausse une fois pour qu’elle soit fausse tout le temps. Une proposition peut être soit vraie soit fausse.
Un seul contre-exemple suffit donc à montrer qu’une proposition est fausse.
Exemples
Considérons en guise d’exemples les deux propositions qui suivent.
1) “Tous les nombres impairs supérieur à 101 sont des nombres premiers.”
Pour rappel, un nombre premier est un nombre qui est divisible uniquement par 1 et par lui même, comme 13 par exemple alors que 15 ne l’est pas (car divisible par 3 par exemple).
Pour prouver que la proposition est fausse, on cherche un nombre impair supérieur à 101 qui n’est pas premier.
Regardons par exemple 105.
105 est un nombre impair, divisible par 5. Il n’est donc pas premier mais est supérieur à 101.
105 est un contre-exemple : La proposition est donc fausse.
2) “Si $x^2 > 9$ alors $x > 3$”.
Regardons par exemple le nombre $x = -4$.
On a $x^2 = (-4)^2 = 16 > 9$ mais $ x = -4 < 3$.
$-4$ est un contre-exemple et la proposition est donc fausse.
Raisonnement par disjonction de cas
Raisonnement par disjonction de cas
Principe
Pour prouver qu’une proposition est vraie sur un ensemble $E$, on peut monter qu’elle est vraie sur des sous-ensembles disjoints de $E$, dont la réunion est $E$.
Le raisonnement par disjonction de cas consiste donc à séparer différents cas.
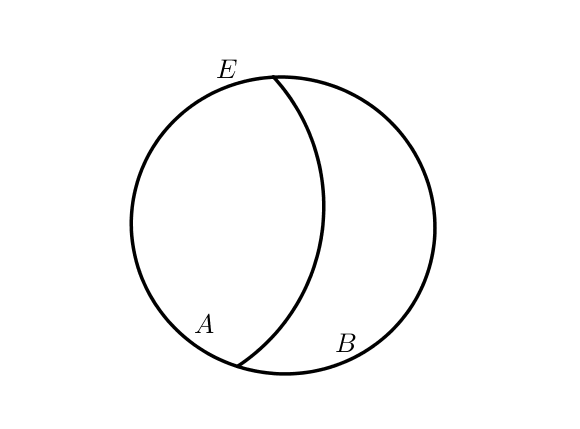
Illustration graphique
Dans l’exemple ci-dessous, les deux sous-ensembles $A$ et $B$ sont séparés et en les réunissant, on obtient la totalité de $E$.
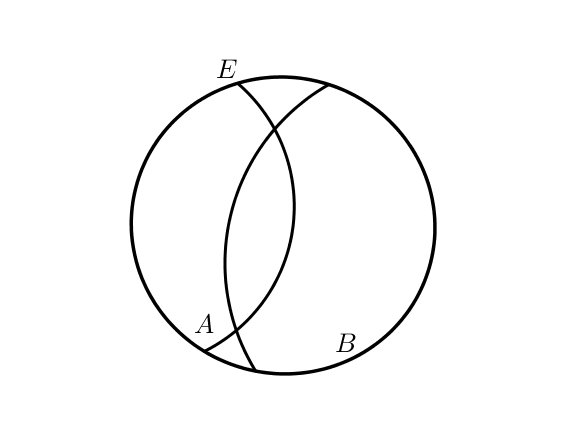
Dans ce deuxième exemple, les deux sous-ensembles ne sont pas tout à fait séparés dans la mesure où il existe une partie commune, mais la réunion est toujours égale à $E$. Dans ce cas, on ne pourrait pas raisonner par disjonction de cas.
Exemple :
On souhaite, en guise d’exemple, montrer que la proposition suivante $P$ est vraie :
“Pour tout entier naturel $n$, $\dfrac{n(n + 1)}{2}$ est un entier”.
Pour montrer cette proposition, on raisonne par disjonction de cas.
On sépare les entiers naturels en deux-sous ensembles, les entiers pairs et les entiers impairs.
En effet, un entier est soit pair, soit impair mais il ne peut être les deux à la fois : ces deux ensembles sont donc disjoints mais leur réunion forme l’ensemble des entiers naturels.
Premier cas : on suppose que $n$ est pair.
Il existe donc un entier naturel $k$ tel que $n = 2k$, car $n$ est divisible par $2$.
Ainsi,
$\dfrac{n(n+1)}{2} = \dfrac{2k(2k+1)}{2}$
$\dfrac{n(n+1)}{2}= k(2k +1)$ qui est un entier.
Deuxième cas : on suppose que $n$ est impair.
Il existe donc un entier naturel $k$ tel que $n = 2k + 1$. (Par exemple, $17 = 2 \times 8 + 1$).
Ainsi,
$\dfrac{n(n+1)}{2} = \dfrac{(2k+1)(2k+1 + 1)}{2}$
$\dfrac{n(n+1)}{2} = \dfrac{(2k+1)(2k+2)}{2} $
$\dfrac{n(n+1)}{2} = \dfrac{2(2k+1)(k+1)}{2} $
$\dfrac{n(n+1)}{2} = (2k +1)(k + 1)$ qui est un entier.
Conclusion :
Dans tous les cas, pour tout $n \in \mathbb{N}, \dfrac{n(n+1)}{2}$ est un entier donc la propriété $P$ est vraie pour tout entier.
Raisonnement par l'absurde
Raisonnement par l’absurde
Principe :
Pour montrer qu’une proposition est vraie, on peut supposer qu’elle est fausse et montrer que l’on arrive alors à une contradiction, c’est à dire une incohérence.
Exemple
On souhaite démonter que “Zéro n’admet pas d’inverse”.
Pour rappel, l’inverse d’un nombre $a$ est le nombre $b$ tel que $a \times b = 1$.
Débutons notre raisonnement par l’absurde en supposant que $0$ ait un inverse.
Il existe alors un nombre $a$ tel que
$a \times 0 = 1$.
Or $0 + 0 = 0$
On peut donc écrire que $a \times (0 + 0) = 1$.
On obtient alors l’égalité suivante :
$a \times 0 = a \times (0 + 0) = a \times 0 + a \times 0 = 1 + 1 = 2$.
Or on a supposé que $a \times 0 = 1$
On obtient alors $1 = 2$, ce qui constitue une contradiction.
Ainsi, $0$ n’admet pas d’inverse.

