Schéma de Bernoulli et loi binomiale
Schéma de Bernoulli et loi binomiale
Définition
On appelle schéma de Bernoulli de paramètres $n$ et $p$ la répétition de $n$ expériences de Bernoulli de paramètre $p$, les répétitions étant indépendantes.
Exemple
On lance 2 fois un dé : on répète deux fois la même expérience qui consiste à lancer le dé.
On appelle ici succès (noté $S$ )le fait d’obtenir 1 lors d’un lancé.
Ainsi la probabilité du succès est $\dfrac{1}{6}$ et celle de l’échec $\dfrac{5}{6}$.
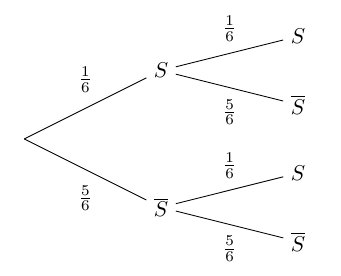
C’est donc un schéma de Bernoulli de paramètres $n = 2$ et $p = \dfrac{1}{6}$.
Un schéma de Bernoulli se représente toujours par un arbre.
On définit à partir d’un schéma de Bernoulli une loi binomiale.
Loi binomiale
On réalise un schéma de Bernoulli de paramètres $n$ et $p$.
On définit une variable aléatoire en posant $X$ qui compte le nombre de succès au cours des $n$ répétitions.
$X$ varie de 0 (c’est à dire 0 succès) à $n$ (c’est à dire uniquement des succès).
La loi de probabilité de $X$ s’appelle la loi binomiale de paramètres $n$ et $p$.
Elle est notée $\mathcal{B}(n;p)$
Exemple
Reprenons l’exemple précédent. Il s’agit d’une loi binomiale de paramètres $n = 2$ et $p = \dfrac{1}{6}$
$X$ suit donc la loi binomiale : $\mathcal{B}(2;\dfrac{1}{6})$
| $X=$ | $0$ | $1$ | $2$ |
| Proba | $p(X=0)$ | $p(X=1)$ | $p(X=2)$ |
Expérience et loi de Bernoulli
Expérience et loi de Bernoulli
Définition
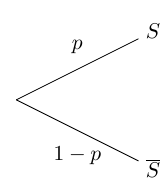
Une expérience de Bernoulli est une expérience aléatoire possédant deux issues possibles :
– le succès $S$ de probabilité $p$
– l’échec $\overline{S}$ de probabilité $1 – p$
Une expérience de Bernoulli peut se représenter par un arbre.
Exemple
On lance un dé équilibré.
On définit le succès $S$ comme étant l’issue “obtenir 6”.
L’échec $\overline{S}$ correspond donc au fait d’obtenir un autre nombre que 6.
La probabilité du succès $p$ vaut $\dfrac{1}{6}$.
Loi de Bernoulli :
A partir d’une expérience de Bernoulli on peut définir une variable aléatoire $X$ en posant :
– $X = 1$ pour le succès
– $X = 0$ pour l’échec
On dira alors que $X$ suit la loi de Bernoulli de paramètre $p$.
On peut représenter les valeurs de $X$ dans un tableau avec leur probabilité associée.
| Valeurs | $0$ | $1$ |
| probabilités | $1-p$ | $p$ |
Espérance et écart-type
L’espérance de $X$ est $E(X) = p$ et son écart-type est $ \sigma(X) = \sqrt{p(1 – p)}$.
Formules de la loi binomiale
Formules de la loi binomiale
On considère une expérience suivant un schéma de Bernoulli de paramètres $n$ et $p$. Un schéma de Bernoulli est la répétition de $n$ expériences de Bernoulli indépendantes de paramètre $p$, la probabilité du succès.
La variable aléatoire associée est $X$ et compte le nombre de succès au cours des $n$ répétitions.
On notera alors que $X$ suit la loi $\mathcal{B}(n; p)$.
De plus, $X$ est compris entre 0 et $n$.
Calculs de probabilités
La probabilité d’obtenir exactement $k$ succès vaut :
$P(X = k) = \left ( \begin{array}{c} n \\ k \\ \end{array} \right ) p^k \ (1 – p)^{n – k}$.
Espérance, écart-type
L’espérance d’une loi binomiale est $E(X) = n \times p$ et son écart-type vaut $\sigma(X) = \sqrt{np(1-p)}$.
Exemple :
On lance un dé quatre fois. On cherche la probabilité d’obtenir trois fois le nombre 6.
On répète donc quatre fois de manière indépendante l’expérience de Bernoulli de paramètre $p = \dfrac{1}{6}$.
En effet, lors d’un lancé, la probabilité d’obtenir un 6 est $p = \dfrac{1}{6}$.
On définit ainsi un schéma de Bernoulli de paramètres $n = 4$ et $p = \dfrac{1}{6}$.
$X$ suit donc une loi $\mathcal{B} \left (4; \dfrac{1}{6} \right)$.
Ainsi, on cherche à calculer $P(X = 3)$.
En appliquant la formule,
$ P(X = 3) = \left ( \begin{array}{c} 4 \\ 3 \\ \end{array} \right ) \left(\dfrac{1}{6} \right )^3 \left (1 – \dfrac{1}{6} \right )^{4 – 3}$
$ P(X = 3) =4 \times \dfrac{1}{6^3} \times \dfrac{5}{6} $
$ P(X = 3) =\dfrac{20}{6^4} \approx 0,015 $
Ainsi, la probabilité d’obtenir trois fois le nombre 6 est de 0,015 soit 1,5%.
Loi binomiale - Schéma
Loi binomiale – Schéma
Considérons la loi binomiale de paramètres $n = 3$ et $p = \dfrac{1}{6}$.
Cela signifie que l’on répète trois fois l’expérience et que la probabilité du succès est $\dfrac{1}{6}$.
Un arbre pondéré est utile pour représenter la loi binomiale.
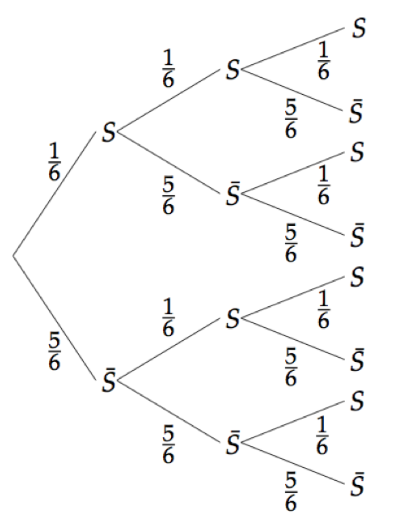
La variable aléatoire associée à la loi binomiale est $X$. Cette dernière permet de compter le nombre de succès.
En considérant le premier chemin par exemple, on rencontre trois fois la lettre $S$ : ainsi, $X = 3$.
Ainsi, $X$ est compris entre 0 et 3.
L’arbre permet de calculer des probabilités.
Exemple
Calculons $P(X = 3)$.
En regardant l’arbre, on remarque que cet événement n’a lieu qu’une fois.
Pour obtenir la probabilité associée, il faut alors multiplier entre elles les probabilités inscrites sur les branches parcourues;
$P(X = 3) = \dfrac{1}{6} \times \dfrac{1}{6} \times \dfrac{1}{6} = \dfrac{1}{216}$.
Calculons de même $P(X = 1)$. L’événement associé a lieu 3 fois.
Ainsi, $P(X = 1) =\left ( \dfrac{5}{6} \right )^2 \times \dfrac{1}{6} + \left ( \dfrac{5}{6} \right )^2 \times \dfrac{1}{6} +\left ( \dfrac{5}{6} \right )^2 \times \dfrac{1}{6} =3 \times \left ( \dfrac{5}{6} \right )^2 \times \dfrac{1}{6}$.
Il existe une formule qui permet de simplifier ce calcul. Les calculatrices permettent aussi ces calculs


