Espérance et écart-type
Espérance et écart-type
Définition :
Soit $X$ une variable aléatoire de loi de probabilité suivante :
| Valeurs | $x_1$ | $x_2$ | … | $x_n$ |
| Probabilités | $p_1$ | $p_2$ | … | $p_n$ |
Espérance de $X$ :
$E(X) = x_1p_1 + x_2p_2 + … + x_np_n$
Variance de $X$ :
$V(x) = p_1 \times [x_1 – E(X)]^2 + p_2 \times [x_2 – E(X)]^2 + … + p_n \times [x_n – E(X)]^2$
Ecart type de $X$ :
$\sigma(X) = \sqrt{V(X)}$.
Exemple :
On considère la variable aléatoire $X$ représentant le gain d’un joueur (en €) et ayant comme loi de probabilité le tableau suivant:
| Valeurs | 4 | 1 | -2 |
| Probabilités | $\dfrac{1}{4}$ | $\dfrac{1}{2}$ | $\dfrac{1}{4}$ |
Calculons l’espérance de $X$:
$E(X) = 4 \times \dfrac{1}{4} + 1 \times \dfrac{1}{2} + (-2) \times \dfrac{1}{4} = 1$.
Cela signifie qu’en moyenne, le joueur peut espérer gagner 1€ par partie en jouant de nombreuses fois.
Calculons la variance de $X$:
$V(X) = \dfrac{1}{4} \times [4 – 1]^2 + \dfrac{1}{2} \times [1 – 1]^2 + \dfrac{1}{4} \times [-2 – 1]^2 = \dfrac{9}{2}$.
Enfin, l’écart type vaut :
$\sigma(X) = \sqrt{\dfrac{9}{2}} \approx 2,12$.
L’écart type permet de mesurer l’écart à l’espérance des valeurs.
Propriétés :
Soient $X$ une variable aléatoire, $a$ et $b$ deux réels,
$E(aX + b) = aE(X) + b$
$V(aX) = a^2 V(X)$.
Variable aléatoire
Variable aléatoire
Définition :
On appelle variable aléatoire toute grandeur numérique qui dépend des résultats d’une expérience aléatoire.
Soit $X$ une variable aléatoire prenant comme valeurs $x_1, x_2,…, x_n$,
La loi de probabilité de $X$ est la donnée de ce tableau:
| Valeurs | $x_1$ | $x_2$ | … | $x_n$ |
| Probabilités | $p(X=x_1)$ | $p(X=x_2)$ | … | $p(X=x_n)$ |
Ce tableau contient sur la première ligne toutes les valeurs que peut prendre la variable aléatoire et sur la seconde les probabilités correspondantes.
La somme de toutes les probabilités vaut 1.
Exemple :
On lance deux fois de suite une pièce équilibrée.
Les issues possibles, c’est à dire l’univers, sont $\Omega = \{PP, PF, FP, FF\}$.
Chacune de ces issues possède une probabilité de réalisation de $\dfrac{1}{4}$.
Selon le côté de la pièce, les gains varient:
+2€ si PILE apparait
-1€ si FACE apparait
On pose alors $X =$ le gain du joueur.
On cherche à établir la loi de probabilité de $X$.
On commence donc par trouver toutes les valeurs possibles de $X$ :
$PP \to +2 +2 = +4$€
$PF \to -1 + 2 = +1$€
$FP \to +2 – 1 = +1$€
$FF \to -1 – 1 = -2$€
Ainsi les valeurs de $X$ sont $+4, +1, -2$.
Calculons par exemple $p(X = 1)$: il s’agit de la probabilité d’obtenir 1€.
Ainsi, $p(X = 1) = \dfrac{1}{4} + \dfrac{1}{4}$.
La loi de probabilité de $X$ est donc :
| Valeurs | $4$ | $1$ | $-2$ |
| Probabilités | $\dfrac{1}{4}$ | $\dfrac{1}{2}$ | $\dfrac{1}{4}$ |
Formules de la loi binomiale
Formules de la loi binomiale
On considère une expérience suivant un schéma de Bernoulli de paramètres $n$ et $p$. Un schéma de Bernoulli est la répétition de $n$ expériences de Bernoulli indépendantes de paramètre $p$, la probabilité du succès.
La variable aléatoire associée est $X$ et compte le nombre de succès au cours des $n$ répétitions.
On notera alors que $X$ suit la loi $\mathcal{B}(n; p)$.
De plus, $X$ est compris entre 0 et $n$.
Calculs de probabilités
La probabilité d’obtenir exactement $k$ succès vaut :
$P(X = k) = \left ( \begin{array}{c} n \\ k \\ \end{array} \right ) p^k \ (1 – p)^{n – k}$.
Espérance, écart-type
L’espérance d’une loi binomiale est $E(X) = n \times p$ et son écart-type vaut $\sigma(X) = \sqrt{np(1-p)}$.
Exemple :
On lance un dé quatre fois. On cherche la probabilité d’obtenir trois fois le nombre 6.
On répète donc quatre fois de manière indépendante l’expérience de Bernoulli de paramètre $p = \dfrac{1}{6}$.
En effet, lors d’un lancé, la probabilité d’obtenir un 6 est $p = \dfrac{1}{6}$.
On définit ainsi un schéma de Bernoulli de paramètres $n = 4$ et $p = \dfrac{1}{6}$.
$X$ suit donc une loi $\mathcal{B} \left (4; \dfrac{1}{6} \right)$.
Ainsi, on cherche à calculer $P(X = 3)$.
En appliquant la formule,
$ P(X = 3) = \left ( \begin{array}{c} 4 \\ 3 \\ \end{array} \right ) \left(\dfrac{1}{6} \right )^3 \left (1 – \dfrac{1}{6} \right )^{4 – 3}$
$ P(X = 3) =4 \times \dfrac{1}{6^3} \times \dfrac{5}{6} $
$ P(X = 3) =\dfrac{20}{6^4} \approx 0,015 $
Ainsi, la probabilité d’obtenir trois fois le nombre 6 est de 0,015 soit 1,5%.
Loi binomiale - Schéma
Loi binomiale – Schéma
Considérons la loi binomiale de paramètres $n = 3$ et $p = \dfrac{1}{6}$.
Cela signifie que l’on répète trois fois l’expérience et que la probabilité du succès est $\dfrac{1}{6}$.
Un arbre pondéré est utile pour représenter la loi binomiale.
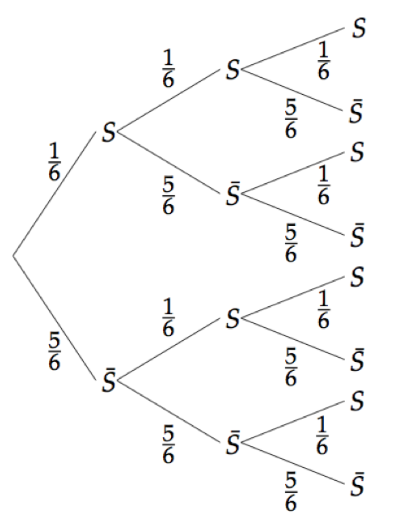
La variable aléatoire associée à la loi binomiale est $X$. Cette dernière permet de compter le nombre de succès.
En considérant le premier chemin par exemple, on rencontre trois fois la lettre $S$ : ainsi, $X = 3$.
Ainsi, $X$ est compris entre 0 et 3.
L’arbre permet de calculer des probabilités.
Exemple
Calculons $P(X = 3)$.
En regardant l’arbre, on remarque que cet événement n’a lieu qu’une fois.
Pour obtenir la probabilité associée, il faut alors multiplier entre elles les probabilités inscrites sur les branches parcourues;
$P(X = 3) = \dfrac{1}{6} \times \dfrac{1}{6} \times \dfrac{1}{6} = \dfrac{1}{216}$.
Calculons de même $P(X = 1)$. L’événement associé a lieu 3 fois.
Ainsi, $P(X = 1) =\left ( \dfrac{5}{6} \right )^2 \times \dfrac{1}{6} + \left ( \dfrac{5}{6} \right )^2 \times \dfrac{1}{6} +\left ( \dfrac{5}{6} \right )^2 \times \dfrac{1}{6} =3 \times \left ( \dfrac{5}{6} \right )^2 \times \dfrac{1}{6}$.
Il existe une formule qui permet de simplifier ce calcul. Les calculatrices permettent aussi ces calculs


