Suites numériques, variations
Suites numériques, variations
Les différentes façons de définir une suite
La première définition est la définition explicite, c’est à dire que $u_n$, le terme de rang $n$, est exprimé directement en fonction de $n$ comme par exemple $u_n = 3n + 2$, $u_n$ s’écrit donc sous la forme : $u_n = f(n)$.
Une autre manière de définir une suite est la définition par récurrence, c’est-à-dire que $u_{n + 1}$ est défini en fonction de $u_n$ comme :
$\left \{ \begin{array}{l} u_0 = 1 \\ u_{n + 1} = 2u_n – 5 \\ \end{array} \right.$
On a bien : $u_{n + 1} = f(u_n)$ (avec $f(x)=2x-5$).
Pour trouver un terme de la suite, il faut avoir d’abord calculé ceux qui le précèdent.
Enfin, il est possible de définir une suite de manière implicite dans des problèmes de géométrie ou d’économie par exemple.
Majorant, minorant
Si pour tout $n \in \mathbb{N}, \ u_n \leq M$ alors $M$ est un majorant de la suite.
Si pour tout $n \in \mathbb{N}, \ u_n \geq m$ alors $m$ est un minorant de la suite.
Si une suite est à la fois minorée et majorée (comprise entre $m$ et $M$), elle est bornée.
Les variations
Si pour tout $n \in \mathbb{N}, \ u_{n + 1} \geq u_n$ alors $(u_n)$ est croissante.
Si pour tout $n \in \mathbb{N}, \ u_{n + 1} \leq u_n$ alors $(u_n)$ est décroissante.
Suites arithmétiques - Définition
Suites arithmétiques
Définition
Une suite arithmétique est une suite pour laquelle chaque terme permet de déduire le suivant en lui ajoutant le même nombre : la raison $r$.
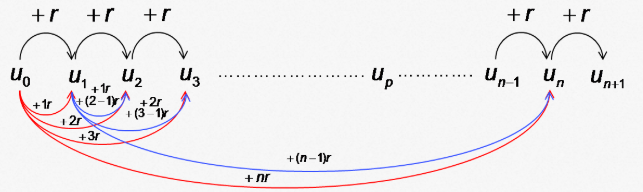
Pour définir une suite arithmétique $(u_n)_{(n \in \mathbb{N})}$, il faut un premier terme, $u_0$ généralement, et la raison $r$ ($r \in \mathbb{R}$).
On écrit alors : $\left \{ \begin{array}{l} u_{n + 1} = u_n + r \\ u_0 \\ \end{array} \right.$
Exemple :
Considérons la suite $\left \{ \begin{array}{l} u_{n + 1} = u_n – 7 \\ u_0 = 17 \\ \end{array} \right.$.
On obtient donc $u_1 = 17 – 7 = 10$ et $u_2 = 10 – 7 = 3$.
Cette définition par récurrence ne permet cependant pas de trouver directement n’importe quel terme de la suite : il faut avoir calculé tous les termes précédents.
Il existe néanmoins une formule générale, dite explicite, qui permet de calculer n’importe quel terme de la suite.
Propriétés
Pour tout $n \in \mathbb{N}$ $u_n = u_0 + nr$.
En effet, pour passer de $u_0$ à $u_n$ il faut ajouter $n$ fois la raison.
Si le terme donné de la suite n’est pas $u_0$, la formule plus générale est la suivante :
pour tous $n, \ p \in \mathbb{N}, \ u_n = u_p + (n – p)r$.
En reprenant l’exemple précédent, on peut déterminer $u_7 = u_0 + 7 \times (-7) = -32$
Suites géométriques - Définition
Suites géométriques
1) Définition
Une suite géométrique est une suite pour laquelle chaque terme permet de déduire le suivant en étant multiplié par une constante $q$, la raison.
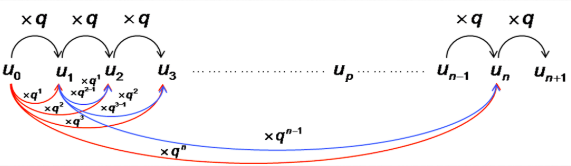
Une suite géométrique est ainsi définie par
$\left \{ \begin{array}{l} u_{n + 1} = u_n \times q \\ u_0 \\ \end{array} \right.$ où $q$ est la raison ($q \in \mathbb{R}$) et $u_0$ est le premier terme de la suite.
Considérons une suite géométrique de raison $2$ de premier terme 5 qui s’écrit alors :
$\left \{ \begin{array}{l} u_{n + 1} = u_n \times 2 \\ u_0=5 \\ \end{array} \right.$
Les premiers termes de la suite sont donc :
$u_1 = u_0 \times 2 = 5 \times 2 = 10$ et
$u_2 = u_1 \times 2 = 10 \times 2 = 20$.
Propriété : expression de $u_n$ en fonction de $n$.
Néanmoins la définition d’une suite géométrique nécessite pour calculer un terme de la suite d’avoir au préalable calculé tous les termes précédents.
Pour passer de $u_0$ à $u_n$, on remarque qu’il a fallu multiplier $u_0$ $n$ fois par $q$ :
Ainsi : $u_n = u_0 \times q^n$ pour tout $n \in \mathbb{N}$.
La formule plus générale permet de calculer tous les termes si l’on ne connait pas le premier terme mais le $p^{\text{ème}}$ :
Pour tous $n, \ p \in \mathbb{N}, u_n = u_p \times q^{(n – p)}$.
En reprenant l’exemple précédent, on trouve $u_4 = u_0 \times q^4 = 5 \times 2^4 = 80$
Sommes de termes de suites arithmétiques et géométriques - Formules
Sommes de termes de suites arithmétiques et géométriques : formules
Sommes de termes de suites arithmétiques
Soit $(u_n)$ une suite arithmétique définie pour tout $n \in \mathbb{N}$ par $\left \{ \begin{array}{l} u_{n + 1} = u_n + r \\ u_0 \end{array} \right.$ où $r$ est la raison ($ r \in \mathbb{R}$).
On souhaite calculer $S_n = u_0 + u_1 + \ … + \ u_n$.
La formule pour calculer cette somme est la suivante : $S_n = \dfrac{(n+1)(u_0 + u_n)}{2}$.
Avant d’appliquer la formule, il faudra prêter une attention particulière au premier terme de la somme ($S_n$ doit commencer par $u_0$).
Il est possible de retenir cette formule, sans toutefois l’écrire sur une copie, sous la forme :
$S_n = \dfrac{\text{(nombre de termes)(premier terme + dernier terme)}}{2}$
Sommes de termes de suites géométriques
Soit maintenant $(u_n)$ une suite géométrique définie pour tout $n \in \mathbb{N}$ par $\left \{ \begin{array}{l} u_{n + 1} = u_n \times q \\ u_0 \end{array} \right.$ où $q$ est la raison ($ q \in \mathbb{R}$).
On souhaite calculer $S_n = u_0 + u_1 + \ … + \ u_n$.
La formule pour calculer cette somme est la suivante : $S_n = \dfrac{u_0 \times \left(1 – q^{(n +1)} \right)}{1 – q}$ avec $q$ différent de 1.
Avant d’appliquer la formule, il faudra prêter une attention particulière au premier terme de la somme ($S_n$ doit commencer par $u_0$).
Il est aussi possible de retenir cette formule, sans toutefois l’écrire sur une copie, sous la forme :
$S_n = \dfrac{\text{(premier terme)(1 – raison}^{\text{nombre de termes}} )}{1 -\text{raison}}$
Comment montrer qu'une suite est arithmétique ?
Comment montrer qu’une suite est arithmétique ?
La seule méthode pour montrer qu’une suite $(u_n)$ est arithmétique consiste à étudier la différence entre le terme $(n + 1)^{\text{ème}}$ de la suite et le $n^{\text{ème}}$ pour tout $n \in \mathbb{N}$ ou encore à étudier la différence : $u_{n + 1} – u_n$.
Si le résultat de cette différence est une constante, la suite est arithmétique, sinon elle ne l’est pas.
Considérons l’exemple suivant : $u_n = 3n – 8$ pour $n \in \mathbb{N}$.
On étudie donc :
$\begin{aligned}u_{n + 1} – u_n &=& 3(n + 1) – 8 – (3n – 8) \\ &=& 3n + 3 – 8 – 3n + 8 \\ &=& 3 \end{aligned}$
Ainsi, $u_{n + 1} – u_n = 3$, la différence est donc une constante donc $(u_n)$ est une suite arithmétique de raison $3$ et de premier terme $u_0 = 3\times 0 – 8 = -8$.
Considérons à présent l’exemple suivant : $u_n = n^2 – 1$ pour $n \in \mathbb{N}$.
On étudie donc :
$\begin{aligned}u_{n + 1} – u_n &=& (n + 1)^2 – 1 – (n^2 – 1) \\ &=& n^2+2n+1-1-n^2+1 \\ &=& 2n+1 \end{aligned}$
Ainsi, $u_{n + 1} – u_n = 2n+1$, la différence n’est donc pas une constante puisque ce résultat dépend de $n$ donc $(u_n)$ n’est pas une suite arithmétique .
Comment montrer qu'une suite est géométrique ?
Comment montrer qu’une suite est géométrique ?
Afin de montrer qu’une suite $(u_n)$ est géométrique, on commence par calculer les premiers termes en s’assurant qu’ils ne sont pas nuls puis on calcule les rapports des premiers termes : $\dfrac{u_1}{u_0}$ et $\dfrac{u_2}{u_1}$.
Considérons par exemple la suite $u_n = 4 \times 3^n$. On a alors $\dfrac{u_1}{u_0} = 3$ et $\dfrac{u_2}{u_1} = 3$.
Si il apparait que le rapport des premiers termes est une constante $q$: on émet alors une conjecture en supposant que la constante ainsi trouvée est la raison de la suite.
Il faut alors montrer en revenant à la définition d’une suite géométrique que $u_{n + 1} = q \times u_n$ pour tout $n \in \mathbb{N}$.
En revenant à notre exemple, on souhaite montrer que $u_{n + 1} = 3 u_n$.
Or :
$3 u_n = 3 \times ( 4 \times 3^n ) $
$3 u_n= 4 \times 3^{n + 1} $
$3 u_n= u_{n + 1}$.
Donc $(u_n)$ est une suite géométrique de raison $3$ et de premier terme $u_0 = 4 \times 3^0 = 4 \times 1 = 4$.


