Angle orienté et lignes trigonométriques
Angle orienté et lignes trigonométriques
Le cercle trigonométrique est un cercle de centre $O$ et de rayon 1.
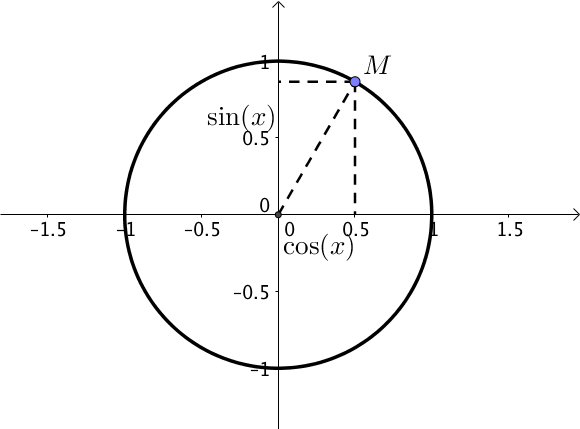
On place le point $M$ sur le cercle défini par un réel en radian, qui correspond à un angle de $\dfrac{\pi}{3}$ ou encore de 60° par rapport à l’axe des abscisses.
Cependant, le point $M$ correspond à d’autres réels. En effet, si on tourne d’un tour autour du cercle, on retrouve le point $M$.
Comme le cercle a un rayon de 1, faire un tour signifie rajouter $2 \pi$.
Ainsi le point $M$ est aussi défini comme le réel $\dfrac{\pi}{3} + 2 \pi = \dfrac{7\pi}{3}$.
Donc le point $M$ correspond à une infinité de point de la forme $\dfrac{\pi}{3} + 2k\pi$ avec $k \in \mathbb{Z}$ ou encore $\dfrac{\pi}{3} (\text{modulo } 2 \pi)$.
Le cosinus correspond à l’abscisse du point $M$ alors que le sinus correspond à son ordonnée.
Application :
On cherche à trouver l’angle entre deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$.
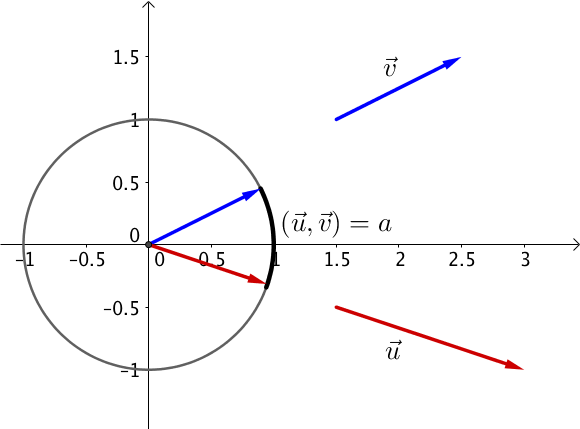
Pour se faire, il faut dans un premier temps les reporter sur le cercle trigonométrique en gardant leur sens et leur direction. L’angle entre les deux vecteurs correspond alors à la longueur de l’arc de cercle compris entre ces deux vecteurs.
On notera ainsi $(\overrightarrow{u}, \overrightarrow{v}) = a + 2k\pi, k \in \mathbb{Z}$.
La mesure principale d’un angle est l’unique valeur de l’angle comprise entre $]- \pi; \pi]$.


