Résolution d'équations trigonométriques
Résolution d’équations trigonométriques
Soit $x$ un réel appartenant au cercle trigonométrique.
On associe à ce réel son cosinus et son sinus.
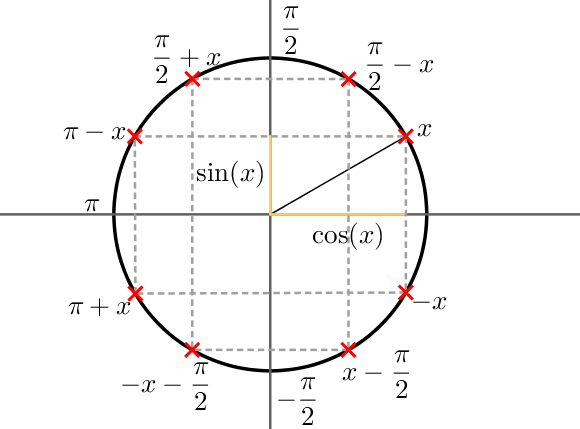
A partir du schéma, on remarque que $\cos \left ( \dfrac{\pi}{2} – x \right ) = \sin(x)$ et $\sin \left ( \dfrac{\pi}{2} – x \right ) = \cos(x)$.
On peut également écrire que $\cos \left ( \dfrac{\pi}{2} + x \right ) = – \sin(x)$ et $\sin \left ( \pi – x \right ) = \sin(x)$.
On peut également retrouver ces formules à partir des formules d’addition.
Les équations trigonométriques
Il s’agit dans un premier temps de résoudre $\cos(x) = \cos(y)$.
Or deux angles ont le même cosinus si et seulement si ils sont égaux ou opposés.
Ainsi, $\cos(x) = \cos(y) \iff \left \{ \begin{array}{c} x = y + 2k \pi \\ x = – y + 2k \pi \end{array} \right. k \in \mathbb{Z}$
L’équation $\sin(x) = \sin(y)$ est équivalente à$ \left \{ \begin{array}{c} x = y + 2k \pi \\ x = \pi – y + 2k \pi \end{array} \right. k \in \mathbb{Z}$


