Vecteurs directeurs d'une droite et équation cartésienne
Vecteurs directeurs d’une droite et équation cartésienne
Définition
Toute droite du plan possède une équation de la forme $ax + by + c = 0$ (avec $a$ ou $b$ non nul) appelée équation cartésienne de la droite.
Réciproquement, l’ensemble des points $M(x, y)$ tel que $ax + by + c = 0$ (avec $a$ ou $b$ non nul) est une droite.
Par exemple, $5x -2y + 1 = 0$ est une équation cartésienne de droite, cependant $10x -4y + 2 = 0$ est aussi une équation de la même droite : on parle donc d’une équation cartésienne, alors qu’il n’existe qu’une seule équation réduite de droite, que l’on trouve en isolant $y$,
$y = \dfrac{5}{2}x + \dfrac{1}{2}$.
Propriété
Une droite d’équation $ax + by + c = 0$ admet comme vecteur directeur $\overrightarrow{u} \left ( \begin{array}{c} -b \\a \end{array} \right )$
Exemple :
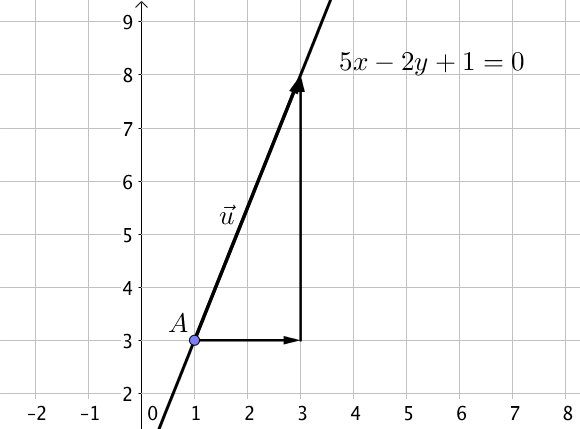
On considère la droite d’équation cartésienne $5x – 2y + 1 = 0$. On souhaite tracer cette droite.
On commence par trouver un vecteur directeur, en appliquant la propriété précédente. $\overrightarrow{u} \left ( \begin{array}{c} 2 \\5 \end{array} \right )$ est un vecteur directeur de la droite.
Il faut ensuite trouver un point appartenant à cette droite.
Pour cela, on choisit une valeur de $x$ quelconque et on calcule la valeur de $y$ correspondante.
Ici, on décide de prendre $x = 1$, et on trouve alors $y = 3$. Le point $A(1; 3)$ appartient donc à la droite.
On place ensuite le point $A$ puis on trace le vecteur directeur à partir de ce point pour obtenir la droite.
Décompositions de vecteurs dans une base
Décompositions de vecteurs dans une base
Lorsque trois points $A, B$ et$ C$ sont non alignés, le triplet $(A; \overrightarrow{AB}; \overrightarrow{AC})$ forme un repère du plan.
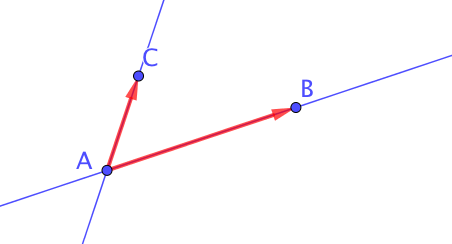
Les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ forment une base du plan et $A$ est l’origine du repère.
Pour mieux visualiser le repère, on peut tracer les axes qui sont les droites $(AB)$ et $(AC)$.
A partir d’un repère quelconque, il est possible de définir les coordonnées d’un point et ceux d’un vecteur.
Théorème
Soit $M$ un point quelconque du plan,
Alors il existe un unique couple de nombres $(x; y)$ tel que $\overrightarrow{AM} = x \overrightarrow{AB} + y \overrightarrow{AC}$.
Le couple $(x; y)$ est les coordonnées de $M$ dans le repère $(A; \overrightarrow{AB}; \overrightarrow{AC})$.
Soit $\overrightarrow{u}$ un vecteur du plan,
Alors il existe un unique couple de nombres $(x; y)$ tel que $\overrightarrow{u} = x \overrightarrow{AB} + y \overrightarrow{AC}$.
Le couple $\left( \begin{array}{c} x \\ y\\ \end{array} \right)$ est les coordonnées de $\overrightarrow{u}$ dans le repère $(A; \overrightarrow{AB}; \overrightarrow{AC})$.
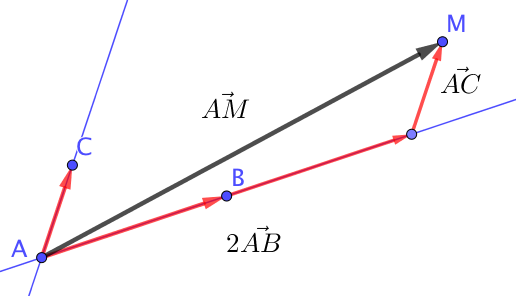
Si l’on doit placer le point $M(2; 1)$, il faut revenir à la définition, c’est à dire $\overrightarrow{AM} = 2 \overrightarrow{AB} + 1 \overrightarrow{AC}$.
On commence alors à tracer le vecteur $2 \overrightarrow{AB}$ puis on lui ajoute $1 \overrightarrow{AC}$, par la méthode des parallélogrammes car les deux vecteurs ont la même origine.
Le vecteur $\overrightarrow{AM}$ est donc la diagonale du parallélogramme ainsi construit et le point $M$ est à l’extrémité de ce vecteur.
Une telle définition permet de se placer désormais dans n’importe quel repère, et donc à partir de n‘importe quelle configuration géométrique, il est possible de définir un repère, permettant de travailler avec les coordonnées.
Vecteurs colinéaires
Vecteurs colinéaires
Définition
Soient $\overrightarrow{u}$ et $\overrightarrow{v}$ deux vecteurs,
$\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires si et seulement si il existe un réel $k$ tel que $\overrightarrow{v} = k \overrightarrow{u}$.
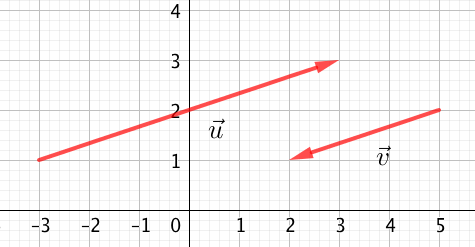
(Dans ce cas, $\overrightarrow{u}=-2\times \overrightarrow{v}$ et le réel $k$ vaut $-2$)
Des vecteurs colinéaires sont portés par des droites parallèles : ils ont donc la même direction mais pas forcément le même sens.
La colinéarité se voit sur un graphique avec la pente des vecteurs, même si cela ne constitue pas une preuve.
Critère de colinéarité (dans un repère)
Soit un repère $(O, \overrightarrow{i}, \overrightarrow{j})$,
Soient deux vecteurs $\overrightarrow{u} \left ( \begin{array}{c} x \\y \\ \end{array} \right )$ et $\overrightarrow{v} \left ( \begin{array}{c} x’ \\ y’ \\ \end{array} \right )$,
$\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires si et seulement si $x\times y’ – y \times x’ = 0$.
Cela revient à dire que les coordonnées des vecteurs sont proportionnelles.
Considérons $\overrightarrow{u} \left ( \begin{array}{c} 3 \\ 2\\ \end{array} \right )$ et $\overrightarrow{v} \left ( \begin{array}{c} 9 \\ 6 \\ \end{array} \right )$, il apparait que $\overrightarrow{v} = 3 \overrightarrow{u}$.
D’après la définition, ces deux vecteurs sont colinéaires.
Si on applique le critère de colinéarité, on trouve $3\times 6 – 2 \times 9 = 18 – 18 = 0$ : les deux vecteurs sont colinéaires.


