Construction de l’image d’un objet par une lentille
Comment construire l’image d’un objet à travers une lentille convergente ?
Voyons trois cas que l’on rencontre régulièrement dans ces constructions d’image d’un objet par une lentille.
Premier cas
Un objet $AB$ est modélisé par une flèche vers le haut pour pouvoir comparer le sens de l’image et celui de l’objet.
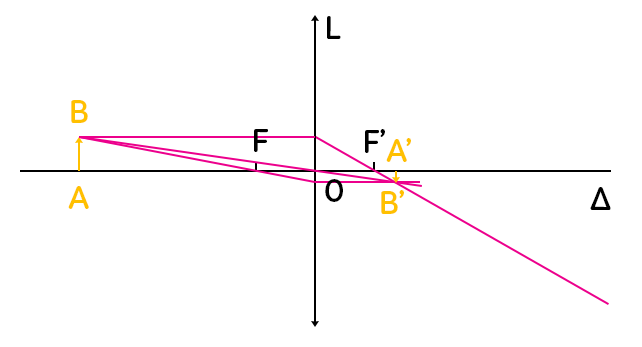
Pour obtenir le tracé de l’image, on trace les trois rayons particuliers qui passent par $B$. Le premier est le rayon qui passe par $B$, qui est parallèle à l’axe optique et qui passe par le foyer $F’$ en sortant de la lentille. Puisqu’on travaille avec des rayons, il faut bien mettre les flèches sur les rayons. On trace ensuite le deuxième rayon, c’est le rayon qui part de $B$ et qui passe par le centre optique, qui lui n’est pas dévié. On obtient alors une intersection et cette intersection correspond à l’image de $B$ par la lentille que l’on appelle $B’$. Pour vérifier que l’on a tracé le bon schéma et la bonne construction, on trace un troisième rayon, celui qui passe par $F$ et qui ressort parallèlement à l’axe optique. On obtient une intersection de ces trois rayons et cette intersection est l’image de $B$ par la lentille notée $B’$. Pour avoir l’image de $A$ par la lentille convergente, on prend la perpendiculaire à l’axe optique qui passe par $B’$. On la note $A’$.
Que remarque-t-on ? L’image est plus petite que l’objet en taille. Cette image est renversée, elle n’a pas le même sens que l’objet. On peut dire que cette image est réelle. Qu’est-ce qu’une image réelle ? C’est une image que l’on peut obtenir sur un écran. On verra que parfois cela ne va pas être le cas et on parlera alors d’image virtuelle.
Deuxième cas
On a rapproché l’objet $AB$ du foyer $F$.
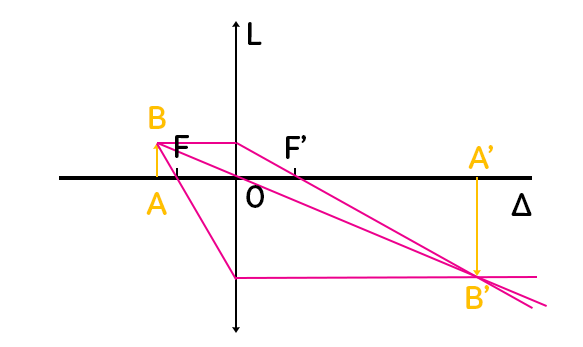
On a fait exactement les mêmes tracés : le rayon parallèle à l’axe optique passant par $B$ et $F’$, le rayon qui passe par le centre optique et qui n’est pas dévié, le rayon qui passe par $F$ et qui ressort parallèlement à l’axe optique. On obtient une image $A’B’$ exactement comme précédemment. On peut dire que l’image est toujours renversée, dans le sens inverse de celui de l’objet. Elle est ici plus grande que l’objet.
Ainsi, on peut avoir les deux cas : plus grande ou plus petite que l’objet. Elle est réelle puisqu’on peut la former sur un écran.
Troisième cas
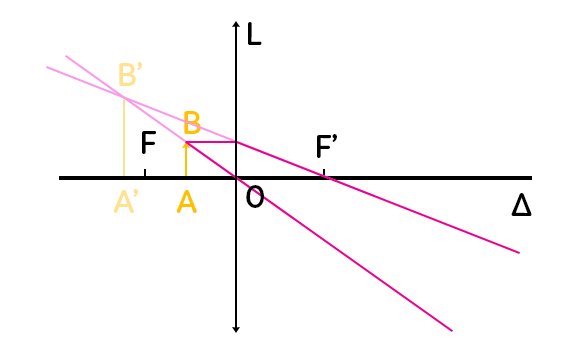
Cette fois-ci on dépasse le foyer $F$. On chercher l’image de l’objet $AB$ mais d’abord l’image de $B$ par la lentille. On trace les premiers rayons : le rayon parallèle à l’axe optique qui ressort par le foyer $F’$, le rayon qui passe par le centre optique de la lentille et qui n’est pas dévié. On se rend compte que ces deux rayons d’éloignent, donc l’intersection ne va pas être à droite, mais à gauche. Pour savoir où est cette intersection, on prolonge ces rayons par des pointillés et à l’intersection de ces deux rayons, on a l’image $B’$ de $B$ par la lentille convergente. On retrouve l’image de $A$ par la lentille convergente en prenant la perpendiculaire à l’axe optique partant de $B’$. On a donc $A’$.
Si on a représenté ces rayons et l’image en pointillés c’est que l’image, cette fois-ci, n’est pas réelle mais virtuelle. Qu’est-ce qu’une image virtuelle ? Une image qu’on ne peut pas observer sur un écran. Cette image est plus grande que l’objet et cette fois-ci dans le même sens que l’objet. Ce cas-ci est assez classique car c’est le cas de la loupe. En effet, c’est une lentille convergente, elle grossit les objets et l’image a le même sens que l’objet.
Relation de conjugaison et grandissement - Ex 1
Relation de conjugaison et grandissement - Ex 2 et 3
Relation de conjugaison de Descartes
Relation de conjugaison de Descartes
Qu’est-ce que la relation de conjugaison de Descartes ?
La relation de conjugaison de Descartes est une relation très importante en optique géométrique.
I. Convention, distances algébriques
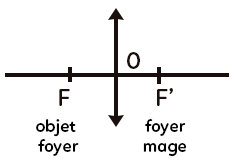
La ligne horizontale correspond à l’axe optique et la lentille ($L$) est représentée par une double flèche verticale. La lentille possède un centre $O,$ un point focal image $F’$ (ou foyer image) et un point focal objet $F$ (ou foyer objet). Les points $F$ et $F’$ sont équidistants de $O.$
Quelle est la convention pour les distances algébriques ?
- On note les distances algébriques avec un trait horizontal au dessus de la distance normale.
- Est compté positif ce qui va de gauche à droite.
- Est compté positif ce qui va de bas en haut.
Exemples
$OF’>0$ distance normale : distance séparant $O$ et $F’$
$\overline{OF’}>0$ distance algébrique positive : pour aller de $O$ à $F’,$ on se déplace selon la convention positive. On a donc $\overline{OF’}=OF’$ (et $OF’$ s’exprime en mètres)
$\overline{OF}<0$ distance algébrique négative : pour aller de $O$ à $F,$ on se déplace selon la convention négative. On a donc $\overline{OF}=-OF$
Définition
$f’=\overline{OF’}$
$f’$ est la distance focale de la lentille : c’est la distance algébrique entre $O$ et $F’.$
$f’$ est positif pour les lentilles convergentes. En effet, pour les lentilles convergentes, le point focal image est à droite du centre de la lentille.
II. Relation de conjugaison de Descartes
L’utilité de la relation de Descartes est de connaître la position de l’image d’un objet à travers une lentille.
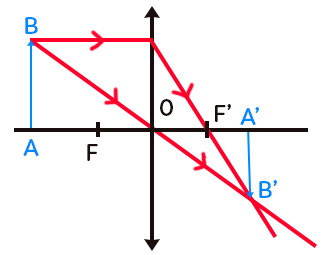
Graphiquement, il est possible de trouver l’image $A’B’$ d’un objet $AB.$ Pour cela, il suffit de faire partir de $B$ des rayons particuliers :
- le rayon passant par $O$ qui n’est jamais dévié ;
- le rayon parallèle à l’axe optique qui ressort de la lentille en passant par le point focal image $F’.$
Le point d’intersection de ces deux rayons particuliers donne $B’,$ l’image de $B$ par la lentille $L.$ On trouve $A’$ l’image de $A$ en projetant verticalement $B’$ sur l’axe optique.
On a donc trouvé graphiquement la position de l’image de $A$ à travers la lentille. Maintenant, il est possible d’utiliser une formule pour trouver la position de $A’$ :
La relation de conjugaison de Descartes $\dfrac{1}{\overline{OA’}}-\dfrac{1}{\overline{OA}}=\dfrac{1}{f’}$
avec $\overline{OA}$: distance algébrique lentille objet.
$\overline{OA’}$: distance algébrique lentille image.
$f’$ : distance focale.
Remarque
$\overline{OA}$, $\overline{OA’}$ et $f’$ sont des distances et s’expriment donc en mètres. Cependant, comme l’équation ne prend en compte que des distances, il est possible de les exprimer en centimètres, en millimètres, etc., du moment que toutes les distances aient la même unité. Attention, l’utilisation des unités autres que celle du système international est possible dans ce cas, mais de manière générale, il est recommandé d’être vigilant sur la cohérence des unités.
Exemple
$f’= 10\text{ cm},$ objet-lentille : $1\text{ m}$
Où est $A’,$ l’image de $A$ par la lentille ?
En utilisant la relation de conjugaison de Descartes, on va isoler $\overline{OA’}$ car c’est la position de $A’$ qui est recherchée.
$\dfrac{1}{\overline{OA’}}-\dfrac{1}{\overline{OA}}=\dfrac{1}{f’}=9{,}0 \text{ m}^{-1}$
On a donc $\overline{OA’}=1{,}1.10^{-1}=11 \text{ cm}$
Remarque
$\dfrac{1}{\overline{OA’}}$ s’exprime en $\text{m}^{-1}$ car c’est $1$ sur des mètres.
L’énoncé donnait la distance objet-lentille. Cependant, l’objet est à gauche de la lentille. Ici, on a donc $\overline{OA}=-1$
$\overline{OA’}>0$ : l’image se situe à droite de $O.$
Grandissement et caractéristique de l’image
Grandissement et caractéristique de l’image
I. Le grandissement
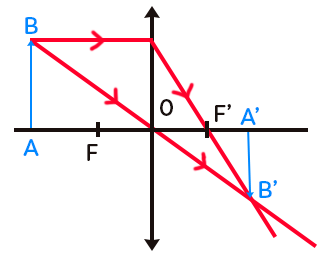
La lentille est représentée avec un chevron de chaque côté : il s’agit ici d’une lentille convergente. On appelle le centre optique $O,$ le point focal objet $F$ et le point focal image $F’.$ L’objet est représenté par $AB.$ On fait partir deux rayons du point $B$ : un passant par le centre optique (non dévié) et un parallèle à l’axe optique (dévié et passant par $F’$).
On constate sur le schéma que l’objet et son image n’ont pas la même taille. Le grandissement correspond au rapport $\dfrac{image}{objet}$. En utilisant également le théorème de Thalès, on a :
$|\gamma| = \dfrac{\overline{A’B’}}{\overline{AB}} = \dfrac{\overline{OA’}}{\overline{OA}}$
Le grandissement est le rapport de la taille de l’image sur celle de l’objet. $\overline{AB}, \overline{A’B’}, \overline{OA}$ et $\overline{OA’}$ sont des distances algébriques : elles peuvent être positives ou négatives.
Remarque : le grandissement est sans unité, à utiliser pour la taille et si l’image est renversée ou non.
II. Position de l’image : réelle vs virtuelle
Comment savoir si une image est réelle ou virtuelle ?
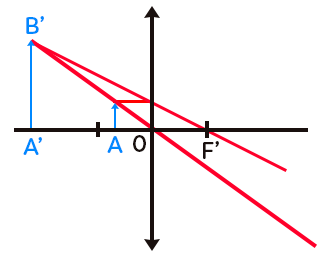
Une image réelle est créée lorsque l’objet $AB$ est placé avant le point focal objet $F.$ On trace les deux mêmes rayons caractéristiques : celui passant par le centre optique et celui parallèle à l’axe optique. Pour une image réelle, $B’$ est l’intersection de rayons réels provenant de $B.$

Une image virtuelle est créée lorsque l’objet $AB$ est entre le point focal objet $F$ et la lentille sur l’axe optique. Les deux rayons tracés ne se croisent pas cette fois. On trouve $B’$ en traçant l’intersection des prolongements des rayons partant de $B$ avant la lentille (côté gauche). L’image virtuelle ne peut pas être observée en plaçant une feuille de papier.
III. La taille de l’image
Renversée ou non
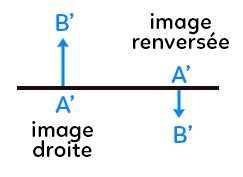
Si $AB$ est vers le haut :
- L’image est droite si $A’B’ > 0$ ($A’B’$ est vers le haut).
- L’image est renversée si $A’B’ < 0$ ($A’B’$ est vers le bas).
Agrandie ou non
Si $|\gamma| > 1,$ l’image est plus grande que l’objet.
Si $|\gamma| = 1,$ l’image est de même taille que l’objet.
Si $|\gamma| < 1,$ l’image est plus petite que l’objet.
Preuve : $|\gamma| = \dfrac{|A’B’|}{|AB|}= \dfrac{A’B’}{AB}$
$|\gamma| > 1 \Leftrightarrow A’B’ > AB$


