Coder une figure
Coder une figure
I) Coder des longueurs
Soit $ABCDE$ un polygone.
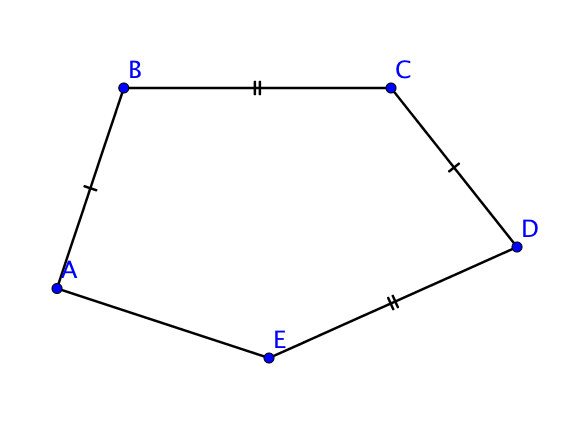
Les deux traits obliques sur la figure présent sur les segment $[BC]$ et $[DE]$ signifient que ces deux segments ont même longueur.
En outre, on voit que $ED = 5$cm, et comme $BC = ED$ on en déduit que $BC = 5$cm également.
Inversement, il est possible que dans l’énoncé, l’information $AB = CD$ apparaisse. Il faut alors la reporter sur le schéma en codant les segments $[AB]$ et $[CD]$ en utilisant un codage différent de celui déjà présent sur la figure car tous les segments ne sont pas égaux, en faisant un seul trait par exemple.
Il existe différents symboles pour signifier l’égalité de longueur : simple trait, double trait, triple trait, des ronds, des vagues,… L’importance est que les segments égaux portent le même codage.
II) Coder des angles
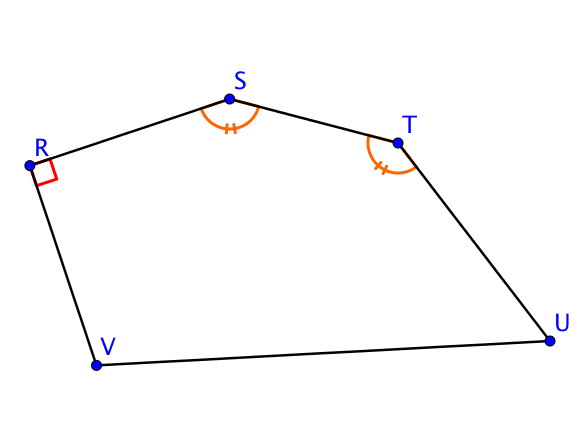
Le codage utilisé au niveau de l’angle $\widehat{SRV}$ signifie qu’il s’agit d’un angle droit ou bien que $\widehat{SRV} = 90$°.
Pour signifier que les angles $\widehat{RST}$ et $\widehat{STU}$ sont égaux, on utilise le même codage au niveau des angles, en utilisant un codage comme celui présent sur la figure par exemple.
Exemples
Il est possible sur une figure de signifier l’égalité d’angles et de longueurs.
Par exemple, on suppose que $ABCD$ est un rectangle.
Si on fait un croquis à main levée, on signifie que le rectangle dispose de quatre angles droits et que les côtés opposés sont égaux par un codage approprié.
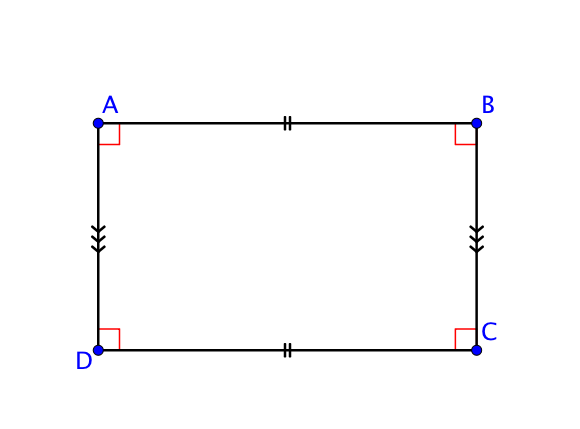
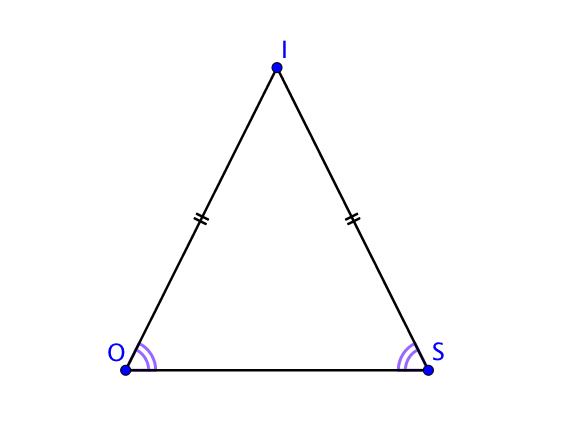
De même, on peut coder le schéma à main levée d’un triangle $ISO$ isocèle en $I$, en indiquant que $IO = IS$ par exemple.
Remarque :
Il faut toutefois se méfier car ce qui est codé n’est pas forcément visible à l’oeil nu, dans le sens où deux longueurs peuvent être égales d’après le codage sans que sur le schéma les deux segments soient de même longueur, ou bien ce que l’on pense voir sur le schéma sans codage n’est pas forcément vrai, c’est à dire que si il n’y a pas de codage, deux segments ne peuvent être égaux.
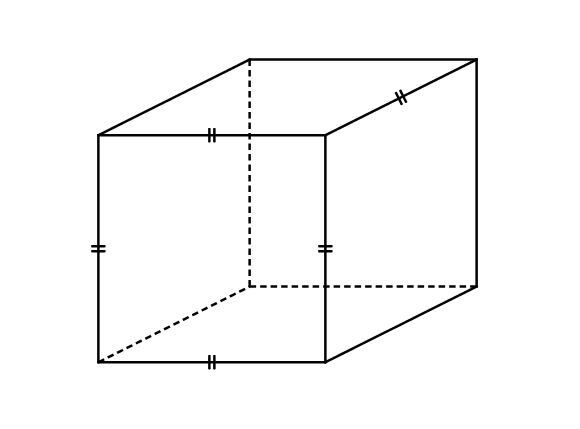
Par exemple, si l’on s’intéresse à un cube, on remarque que seule la face du devant est un vrai carré.
En effet, la perspective fait que les autres faces seront déformées. Même si sur le dessin les longueurs ne sont pas égales, le codage rétablie l’égalité de ces dernières.