Fonction carré
La Fonction carré
Définition
La fonction carré est la fonction qui à tout réel $x$ associe $x^2$, c’est à dire $f(x) = x^2$ pour tout $x \in \mathbb{R}$.
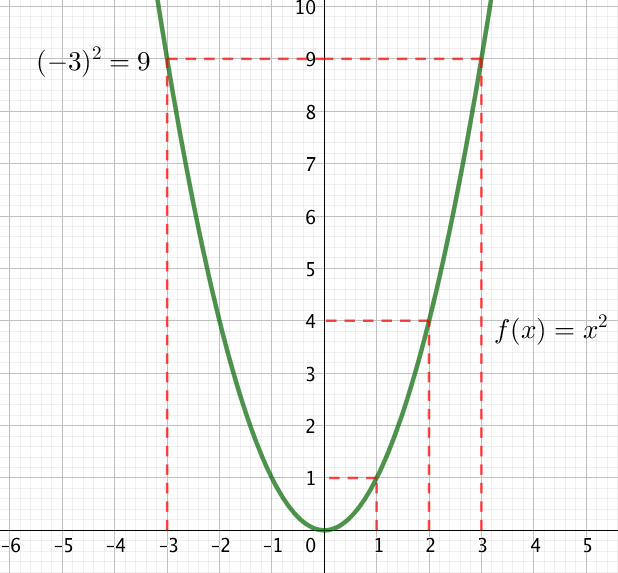
On peut construire sa représentation graphique point par point.
En effet, $0^2 = 0, \ 1^1 = 1, \ 2^2 = 4,…$.
Puis on relit ces différents points.
Sa représentation graphique est une parabole.
Variations
La fonction carré est décroissante pour $x$ négatif et croissante pour $x$ positif.
Son tableau de variation est le suivant :
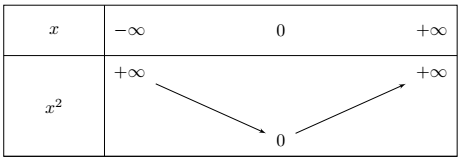
La fonction admet un minimum atteint en $x = 0$. Cette fonction admet un axe de symétrie (l’axe des ordonnées) : c’est une fonction paire.
Résolution graphique d’équations et d’inéquations
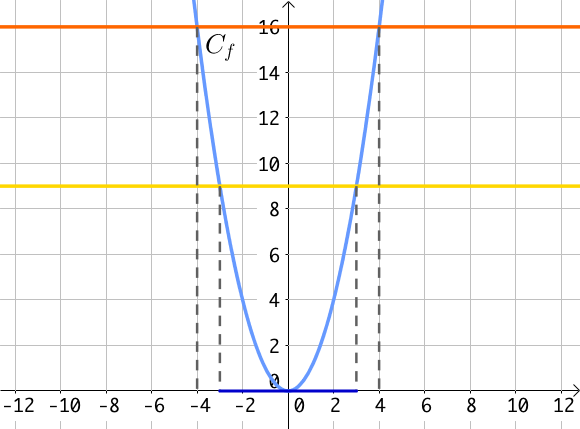
On veut résoudre graphiquement l’équation $f(x) = 16$, c’est à dire on souhaite déterminer les antécédents de 16 par la fonction $f$.
On trace une droite horizontale passant par le point de coordonnées $(0; 16)$ et les solutions de l’équation sont alors les abscisses des points d’intersection entre la droite horizontale et la courbe $C_f$ de la fonction carré.
On trouve alors comme solution $S = \{-4; 4\}$.
On souhaite désormais résoudre l’inéquation $f(x) \leq 9$.
Pour se faire, il faut repérer la portion de courbe pour laquelle les images sont inférieures à $9$ : cela correspond à la zone bleu foncé sur l’axe des abscisses
$S = [-3: 3]$.
Fonction inverse
Fonction inverse
Définition
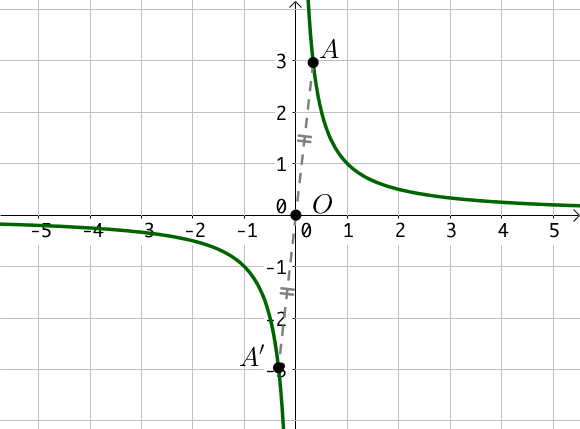
Pour tout $x \in \mathbb{R}^*$, la fonction inverse est la fonction définie par $f(x) = \dfrac{1}{x}$.
On remarquera que l’ensemble de définition de la fonction inverse est $\mathbb{R}^*$ ou encore $\left]-\infty;0\right [\cup \left]0;+\infty\right[$ car on ne peut pas diviser par 0.
La représentation graphique de la fonction inverse est une hyperbole.
Chaque point de la courbe est le symétrique d’un autre par la symétrie centrale de centre $O(0;0)$ : la fonction inverse est une fonction impaire.
Variations
La fonction inverse est décroissante pour $x$ strictement négatif et décroissante pour $x$ strictement positif.
Son tableau de variation est le suivant :
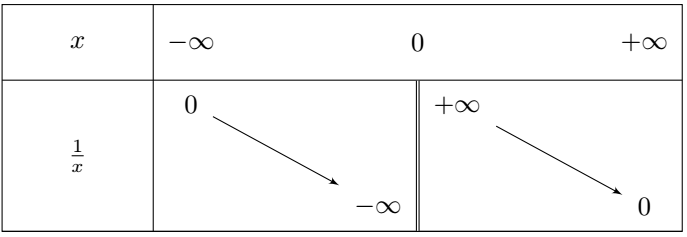
La double barre utilisée signifie que $0$ est une valeur interdite, qui ne peut être prise.
Résolution graphique d’inéquations
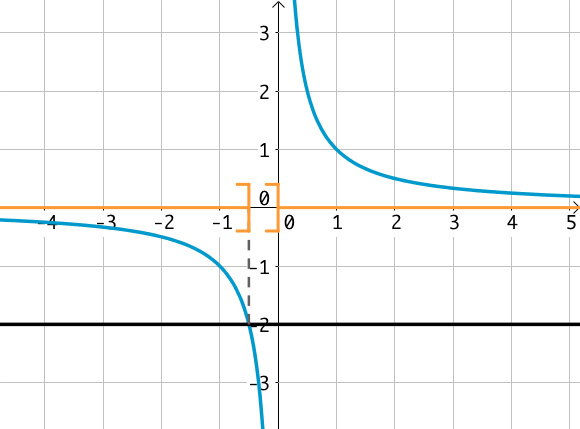
On souhaite par exemple résoudre l’inéquation $f(x) \geq -2$.
On trace pour se faire la droite d’équation $y = -2$ et les solutions sont les antécédents des points de la courbe qui sont au dessus de cette droite.
Graphiquement, les solutions sont donc $S = ]-\infty; -\dfrac{1}{2}]\ \cup \ ]0; +\infty[$ : il s’agit de la réunion de deux intervalles.
Fonction racine carrée
Fonction racine carrée
Définition
Pour tout $x \in [0; +\infty [$, la fonction racine carrée est la fonction $f(x) = \sqrt{x}$.
La racine carrée d’un nombre négatif n’existe pas.
La courbe représentative de la fonction racine carrée est la symétrique par rapport à la droite $y = x$ de la fonction carré pour $x$ positif.
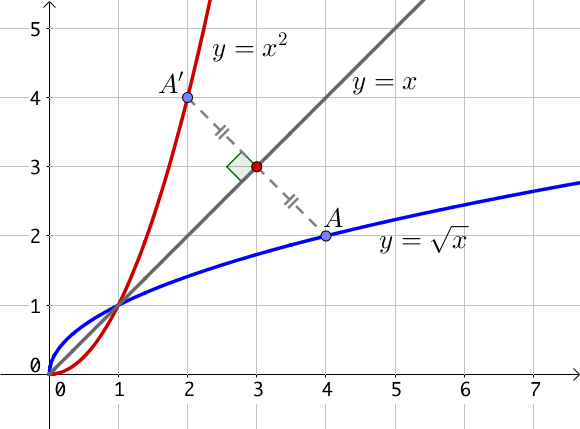
Variations
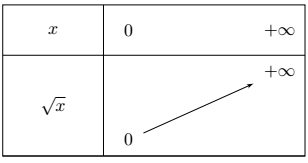
La fonction racine carrée est strictement croissante pour $x$ positif.
Son tableau de variation est le suivant :
Exercice d’Application
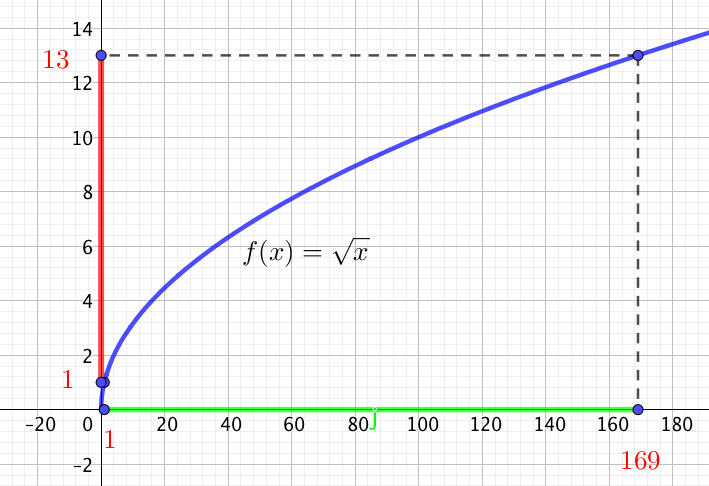
Soit $1 \leq x \leq 169$. Encadrons $\sqrt{x}$.
On sait que la fonction $f$ est croissante pour $x$ positif,
Ainsi, si $1 \leq x \leq 169$ alors $f(1) \leq f(x) \leq f(169)$ (comme $f$ est croissante, le sens des inégalités est préservé)
Ou encore $\sqrt{1} \leq \sqrt{x} \leq \sqrt{169}$
C’est à dire $1 \leq \sqrt{x} \leq 13$.
Voici une représentation graphique pour mieux comprendre :
Fonction du second degré - Le rappel de cours
Fonction du second degré – Le rappel de cours
1) Définition
Pour tout $x \in \mathbb{R}$, une fonction $f$ du second degré peut se mettre sous la forme canonique :
$f(x) = a(x – \alpha)^2 + \beta$, où $a \neq 0$.
2) Variations
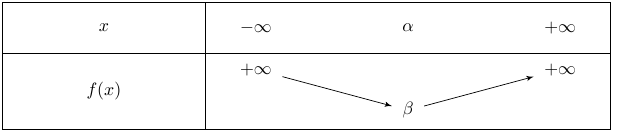
Si $a>0$, la représentation graphique de la fonction est une parabole tournée vers le haut qui admet un minimum atteint en $x= \alpha$ valant $\beta$.
Son tableau de variation est le suivant :
Si $a<0$, la représentation graphique de la fonction est une parabole tournée vers le bas qui admet un maximum atteint en $x= \alpha$ valant $\beta$.
Son tableau de variation est le suivant :
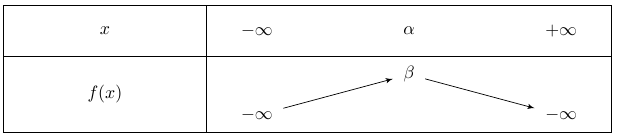
Dans les deux cas, le sommet de la parabole est $S(\alpha; \beta)$.
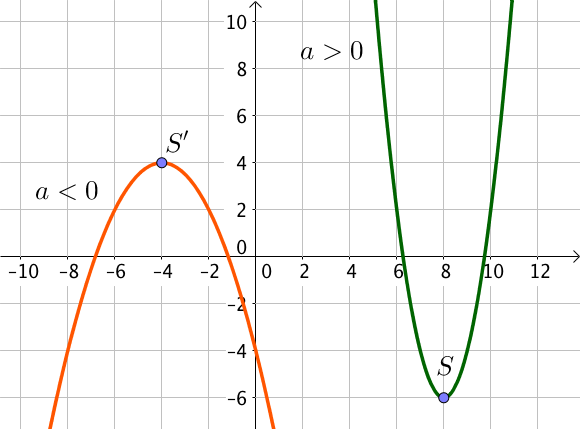
3) Exemple
Soit $f(x) = 2(x + 3)^2 – 4$,
Cette fonction est décroissante puis croissante. Elle admet un minimum ayant pour coordonnées $S(-3; -4)$.
Fonctions linéaires et affines
Fonctions linéaires et affines
Définition
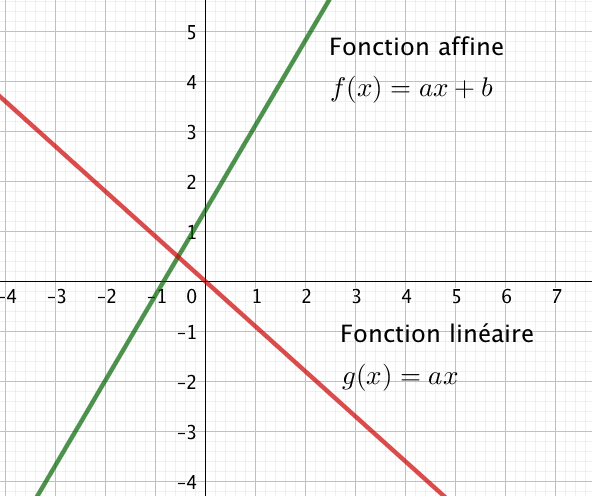
Une fonction affine est une fonction de la forme : $f(x) = ax + b$
Le nombre $a$ est le coefficient directeur de la droite, c’est à dire celui qui donne la pente de la droite, $x$ est la variable.
Le nombre $b$ l’ordonnée à l’origine, c’est à dire la valeur de la fonction lorsque $x = 0$.
Une fonction linéaire est une fonction affine particulière où $b = 0$ :
$g(x) = ax$, il s’agit d’une droite passant par l’origine.
Variations de fonctions affines
Si le coefficient directeur est strictement positif, alors la fonction $f$ est croissante sur $\mathbb{R}$.
Si le coefficient directeur est strictement négatif, alors la fonction $f$ est décroissante sur $\mathbb{R}$.
Si le coefficient directeur est nul, $f$ est constante sur $\mathbb{R}$ dont la représentation graphique est une droite parallèle à l’axe des abscisses.
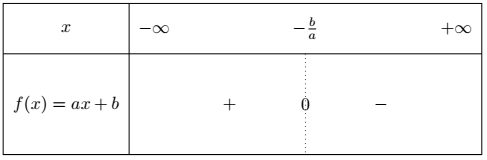
Signe de $f(x)$
On regarde pour quelles valeurs de $x$ la fonction est négative et pour quelles valeurs elle est positive.
Dans les deux cas, si $a \neq 0$, la fonction $f$ s’annule en $x = \dfrac{-b}{a}$.
Si $a>0$, le tableau est le suivant :
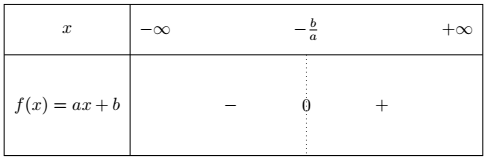
Si $a<0$, le tableau est le suivant :
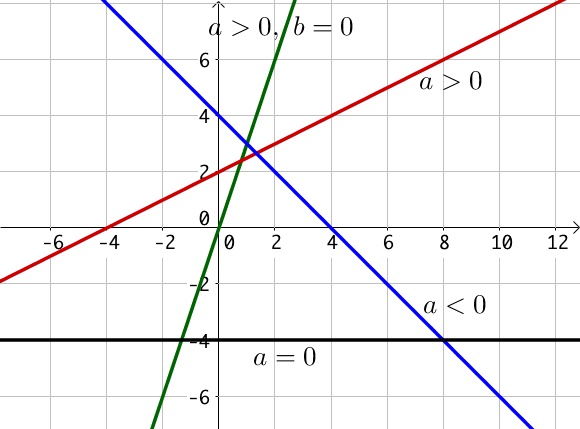
Exemple
La fonction rouge est la fonction $f(x) = 0.5x + 2$. Son ordonnée à l’origine est 2.
Le coefficient directeur vaut $0.5 > 0$ donc $f$ est croissante.
La fonction $f$ s’annule pour $x = \dfrac{-2}{0.5} = -4$. Elle est négative pour $x< -4$ et positive pour $x>-4$.
Fonctions homographiques - Le rappel de cours
Fonctions homographiques
Définition
Pour tout $x \in \mathbb{R} \backslash \left\{\dfrac{-d}{c}\right\}$, on peut définir une fonction homographique comme étant la fonction
$ f(x) = \dfrac{ax+b}{cx+d} $, où $a,b,c$ et $d$ sont des réels. ($c$ et $d$ non tous nuls)
Autre notation
Pour tout $x \in \mathbb{R} \backslash \{\alpha\}$, on peut définir une fonction homographique comme étant la fonction
$ f(x) = \dfrac{a}{x – \alpha} + \beta$, où $a, \alpha, \beta$ sont des réels.
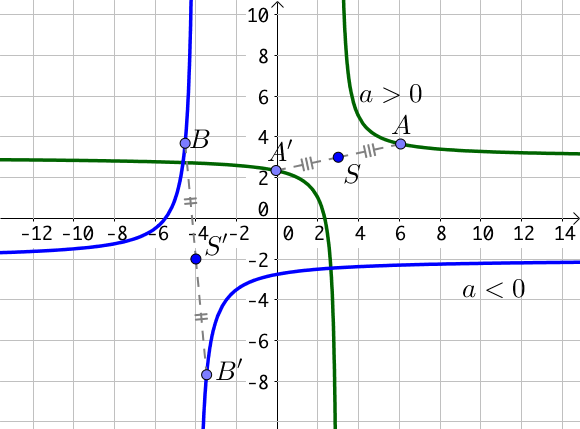
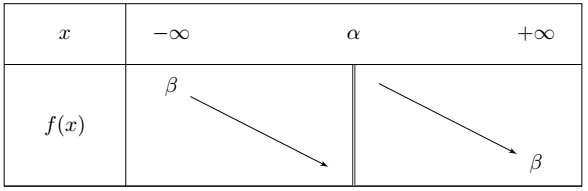
Variations
Les variations sont déterminées à partir du signe de $a$.
Si $a>0$, le tableau de variations est le suivant :
Si $a<0$, le tableau de variations est le suivant :
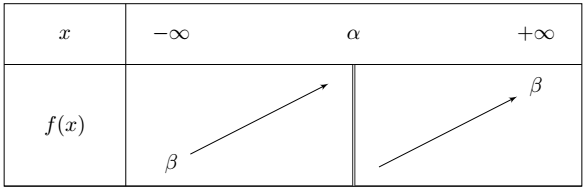
Les doubles barres signifient que la valeur $x = \alpha$ est un valeur interdite car la fonction n’est pas définie pour cette valeur.
Le point $S(\alpha; \beta)$ est le centre de symétrie de l’hyperbole qui est différent de l’origine du repère si $\alpha \neq 0, \beta \neq 0$.