Coordonnées du milieu d'un segment
Coordonnées du milieu d’un segment
Formules
On se place dans un repère.
Soit $I(x_I; y_I)$ le milieu de $[AB]$ avec $A(x_A; y_A)$ et $B(x_B; y_B)$,
Les coordonnées de $I$ sont :
$\left \{ \begin{array}{l} x_I = \dfrac{x_A + x_B}{2} \\ y_I = \dfrac{y_A + y_B}{2} \end{array} \right.$
$ \dfrac{x_A + x_B}{2}$ est appelée une demi-somme.
Exemple
Considérons le schéma suivant et calculons les coordonnées du point $I$ milieu de $[AB]$:
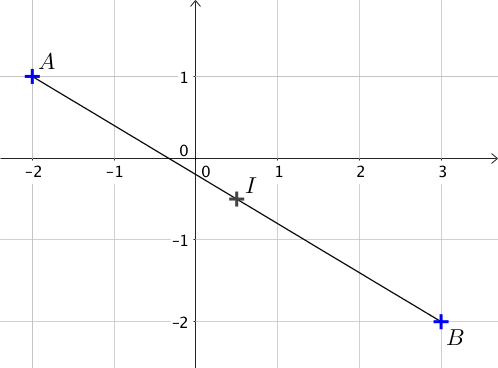
D’après la formule, les coordonnées sont :
$\left \{ \begin{array}{l} x_I = \dfrac{-2 + 3}{2} \\ y_I = \dfrac{1 + (-2)}{2} \end{array} \right.$
Finalement, $I\left(\dfrac{1}{2}; \dfrac{-1}{2}\right)$.
Longueur d’un segment
Longueur d’un segment
Formule
On se place dans un repère orthonormé $(O; I; J)$.
Soient $A(x_A; y_A)$ et $B(x_B; y_B)$ deux points du plan,
la longueur $AB$ est donnée par :
$AB = \sqrt{(x_B – x_A)^2 + (y_B – y_A)^2}$.
Il faudra prêter une attention particulière à l‘ordre lors de la soustraction.
Considérons le schéma suivant et déterminons la longueur $AB$ :
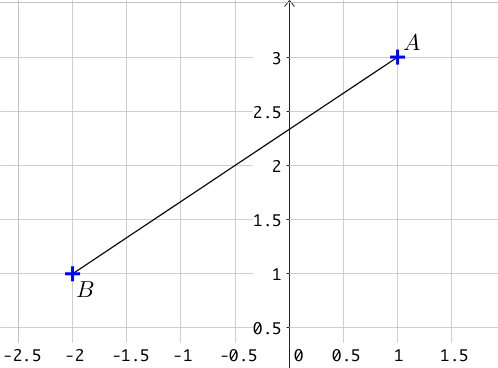
On a:
$AB = \sqrt{(-2 – 1)^2 + (1 – 3)^2} $
$AB= \sqrt{9 + 4} $
$AB= \sqrt{13}$


