Dispersion et réfraction de la lumière
Dispersion et réfraction de la lumière
I. Dispersion de la lumière
La dispersion de la lumière blanche
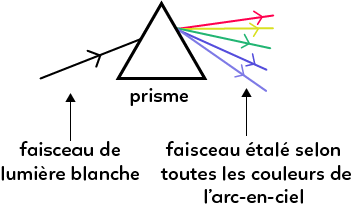
On envoie un faisceau de lumière blanche sur un prisme (c’est un objet en verre). On observe alors à la sortie du prisme un faisceau étalé selon toutes les couleurs de l’arc-en-ciel. Il y a donc une séparation en fonction des longueurs d’onde : cette décomposition est le phénomène de dispersion. La figure obtenue à la sortie du prisme est appelé spectre de la lumière blanche.
La dispersion d’une lumière monochromatique
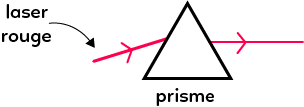
On envoie un laser, par exemple rouge sur un prisme. On observe alors un seul faisceau rouge à la sortie du prisme. Il n’y a pas de décomposition de faisceau. C’est grâce à cette expérience que l’on sait que c’est une lumière monochromatique (une seule couleur). La lumière blanche, quant à elle, est polychromatique (plusieurs couleurs).
Les longueurs d’ondes
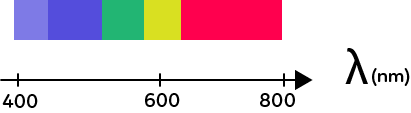
Les couleurs de la lumière sont rattachées à des longueurs d’ondes. Les longueurs d’ondes de la lumière visible vont de 400 nm à 800 nm.
400 nm correspond à une couleur violette et 800 nm à une couleur rouge, et entre il y a les autres couleurs.
II. Réfraction de la lumière
Définition : la réfraction de la lumière est le changement de direction que subit un rayon de lumière lorsqu’il traverse la surface de séparation entre deux milieux transparents.
Un milieu est caractérisé par son indice de réfraction noté $n$ : on peut calculer $n.$ La formule à connaître est : $n=\dfrac{c}{v}$, où $c$ est la célérité de la lumière dans le vide ($3,00\times 10^8 \ m/s$) et $v$ la célérité de la lumière dans le milieu (en $m/s$ ).
En effet la lumière ne va pas à la même vitesse dans le vide que dans l’eau par exemple.
Exemples à connaître :
$n_{air}\simeq 1$
$n_{eau}\simeq 1,33$
$ n_{verre}\simeq 1,5$
Lois de Snell-Descartes
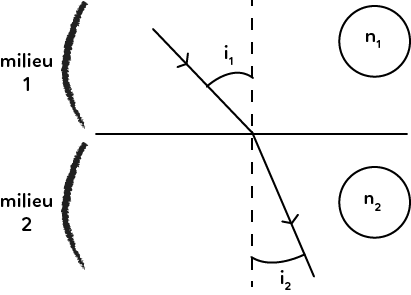
Ce schéma représente le passage d’un rayon lumineux d’un milieu 1 vers un milieu 2. On observe que le faisceau change de direction. Il existe des lois permettant de connaître les angles de réfraction ainsi que les indices de réfraction des milieux. Tout d’abord, il est important de savoir caractériser l’angle d’incidence $i_1$ du faisceau : la référence pour calculer l’angle est la normale à la surface de réfraction (la droite en pointillé).
L’angle d’incidence est donc l’angle entre la normale et le rayon incident. De même l’angle de réfraction $i_2$ est l’angle entre la normale et le rayon réfracté.
Les deux lois à connaître sont donc :
Les rayons incidents, réfractés et la normal sont dans le même plan.
$n_1 \times sin(i_1) = n_2 \times sin(i_2)$.
Attention à bien utiliser la calculette dans le mode radian pour les angles !
Spectres, raies d'émission et d'absorption
Spectres, raies d’émission et d’absorption
I. Spectre d’émission
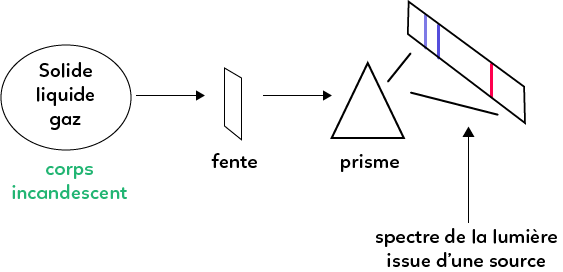
Pour observer un spectre, dans un premier temps, il faut un corps solide, liquide ou gazeux que l’on va chauffer (un corps incandescent) et qui va émettre de la lumière. Après avoir fait passer la lumière émise à travers une fente, la lumière restante va traverser un prisme (un élément qui va disperser les différentes longueurs d’ondes).
Dans cet exemple, on observe trois raies colorées en sortie du prisme, qui correspondent au spectre de la lumière issue de la source. C’est ce qu’on appelle un spectre d’émission.
En fonction de l’objet qui produit la lumière, on distingue deux cas :
– Si c’est un corps chaud (solide, liquide ou un gaz très comprimé), par exemple une étoile qui est un gaz extrêmement chaud et comprimé, alors le spectre est continu. Cela signifie que toutes les couleurs seront présentes, à l’exception de certaines. Pour avoir un spectre continu, il faut avoir l’ensemble des couleurs (rouge, jaune, vert, bleu, violet, etc.) mais plus la source est chaude, plus le spectre s’enrichit en violet. Un spectre continu n’est pas composé de raies.
– Si la source de lumière est un gaz composé d’atomes simples (ou d’ions) qui sont indépendants les uns des autres (il peut y avoir plusieurs atomes différents, mais sans interactions entre eux). Dans ce cas, on observe un spectre de raies d’émission, comme vu avec le schéma. Chaque atome présent dans la source émet un certain nombre de raies et la présence de plusieurs atomes ne change rien au spectre, les raies vont se superposer.
II. Spectre d’absorption
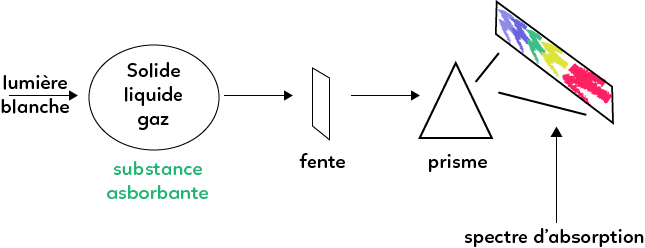
À la différence d’un spectre d’émission, le spectre d’absorption s’intéresse à ce que la source absorbe.
On utilise une lumière blanche qui va être en partie absorbée par le solide/liquide/gaz dont on veut le spectre, ensuite le faisceau passe par une fente, puis par un prisme qui va disperser la lumière, et on observe en sortie le spectre d’absorption.
Supposons dans un premier temps que sur le montage, il n’y a rien qui absorbe. On observe alors en sortie un spectre continu qui correspond au spectre de la lumière blanche. Mais si on interpose un corps (solide, liquide ou gaz) qui va absorber une partie de la lumière, des raies noires vont apparaître dans le spectre, correspondant aux longueurs d’onde absorbées. Les raies noires sont typique du spectre d’absorption.
Le spectre d’absorption d’un gaz sous faible pression est formé de raies noires sur un fond coloré (fond coloré qui correspond au spectre de la lumière blanche).
Si les substances chimiques étudiées sont complexes, ou sous trop haute pression, le spectre ne sera pas forcément composé de raies, mais de bandes beaucoup plus larges. Le spectre n’est alors pas vraiment exploitable.
On remarque qu’un atome donné va émettre des raies précises dans le cas du spectre d’émission, et va en absorber certaines dans le cas du spectre d’absorption. Il sera donc possible d’identifier des identités chimiques.
III. Identification des identités chimiques
La position des raies est caractéristique d’un atome ou d’un ion. On peut donc identifier un atome à partir du spectre des raies. Si on ne dispose que du spectre, on connaît la position des raies, qui sont caractéristiques d’un atome. Il existe des tables identifiant les raies des différents atomes.
Loi de Snell-Descartes
Loi de Snell-Descartes
I. Définitions
L’indice de réfraction d’un milieu donné est noté $n.$ Les milieux sont l’air, l’eau, le verre, le cristal, etc. Chaque milieu qui va pouvoir être traversé par la lumière possède un indice de réfraction.
Il est défini comme étant : $n = \dfrac{c}{v}$.
Avec $c$ la vitesse de la lumière dans le vide ($3,00 \times 10^8 \ m/s$) et $v$ la vitesse de la lumière dans un milieu donné (donnée dans les exercices).
Le dioptre est la surface de séparation entre deux milieux. On imagine une pièce avec de l’air et une fenêtre. La surface de la fenêtre va séparer l’air du verre de la fenêtre : c’est le dioptre. De l’autre côté de la vitre, il y a de nouveau un dioptre entre le verre et l’air extérieur.
La normale est une perpendiculaire.
II. Première loi de Snell-Descartes
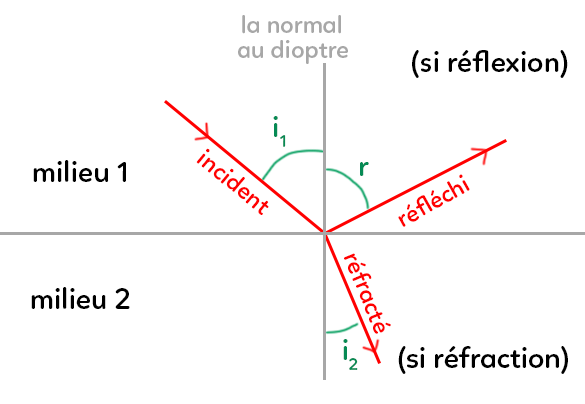
Ce schéma est très important, il faut le connaître et savoir le redessiner. Il est valable pour les deux lois. Dans ce schéma, le trait horizontal est le dioptre. C’est une surface qui sépare les deux milieux (au-dessus et en dessous). Le milieu du dessus s’appelle milieu 1 et celui du dessous milieu 2. Ils sont respectivement caractérisés par leur indice de réfraction $n_1$ et $n_2.$
On envoie un rayon lumineux dans le milieu homogène 1. Le rayon va en ligne droite : c’est le rayon incident. Lorsqu’il arrive au dioptre, il se passe le phénomène de réfraction. Si le rayon est réfracté, c’est qu’il est dévié dans le milieu 2. Le milieu 2 étant aussi un milieu homogène, alors le rayon va aussi en ligne droite. L’angle que le rayon fait avec la normale (perpendiculaire au dioptre) est appelé $i_2.$
L’angle $i_2$ est l’angle de réfraction, tandis que l’angle $i_1$ est l’angle d’incidence.
Il existe une autre possibilité : le rayon peut être réfléchi, il repart du même côté. $r$ est l’angle entre le rayon et la normale : on l’appelle l’angle de réflexion.
Pourquoi les angles se situent entre les rayons et la normale ?
C’est une définition à connaître ! Il peut y avoir soit réflexion, soit réfraction, soit les deux en même temps. La première loi de Snell-Descartes dit que le rayon réfracté et le rayon incident sont dans le plan d’incidence. Le plan d’incidence est le plan formé par la normale et le rayon incident. Deux droites engendrent un plan car elles sont contenues dans ce plan.
III. Deuxième loi de Snell-Descartes
Concernant le rayon réfléchi, la deuxième loi de Snell-Descartes indique que $i_1 = r$.
Concernant le rayon réfracté, on a : $n_1\times sin (i_1) = n_2\times sin (i_2)$. La fonction sinus est sur la calculatrice. On prend toujours le sinus d’un nombre.
Exemple 1
$n_1 = 1,0 \ ;\ n_2 = 1,3 \ ; \ i_1 = 30°.$ Que vaut $i_2$ ?
Dans un premier temps, on calcule le sinus de l’angle $i_2 : sin(i_2) = \dfrac{n_1}{n_2} \times sin(i_1) \approx 3,8.10^{-1}$
Attention car l’angle est en degré ! Il peut être en radian ou en degré, mais il ne faut pas oublier de l’intégrer dans la calculatrice. On va pouvoir maintenant calculer $i_2.$ On doit utiliser la fonction arcsinus.
On a alors : $i_2 = arcsin(3,8.10^{-1}) = 22°$
Exemple 2
On a $n_1 = 1,3 \ ; \ n_2 = 1,0.$ Que vaut l’angle d’incidence limite $i_1$ ?
C’est quelque chose de récurrent qui pourra se retrouver en exercices. C’est un angle particulier qui correspond au moment où l’angle de réfraction correspond à un angle de 90°. C’est l’étape juste avant qu’il y ait réflexion totale.
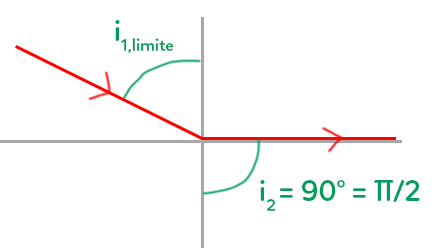
Si jamais on éclaire cette surface d’un rayon qui descend bien verticalement, il ne sera pas dévié. Quand $i_1 = 0, sin(i_1) = 0$ donc $sin(i_2) = 0$ et $i_2 = 0.$
Quand un rayon a un certain angle, il va être dévié, de plus en plus jusqu’à atteindre l’horizontale. On ne peut pas aller au-delà de l’horizontale donc on passe dans la réflexion : c’est la réflexion totale. Quel est cet angle limite où l’on va passer du phénomène de réfraction au phénomène de réflexion ?
Il faut se servir du schéma (voir les notations).
On isole $sin(i_{1,limite}) \ : \ sin(i_{1,limite}) = \dfrac{n_2}{n_1}\times sin(90°) = \dfrac{n_2}{n_1} \approx 7,7.10^{-1}$
$i_{1,limite} = arcsin(7,7.10^{-1}) = 50°$


