Étude de la fonction cosinus
Etude de la fonction cosinus
Domaine de définition et dérivée
La fonction cosinus est définie sur $\mathbb{R}$.
Elle est, en outre, $2\pi$-périodique (ce qui signifie que pour tout $x\in\mathbb{R}, \cos(x+2\pi)=\cos(x)$)
et paire (pour tout $x\in\mathbb{R}, \cos(-x)=\cos(x)$) ce qui permet de restreindre son étude à $[0,\pi]$.
Son domaine de dérivabilité est $\mathbb{R}$ et pour tout $x\in\mathbb{R}, \cos'(x)=-\sin(x)$.
Variations sur $[0,\pi]$
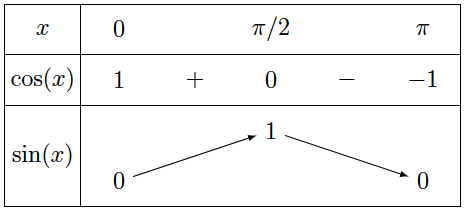
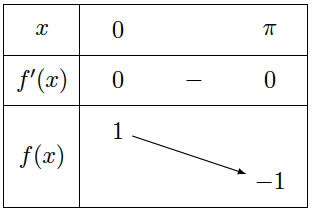
Pour étudier les variations de la fonction cosinus, on étudie le signe de sa dérivée c’est-à-dire le signe de $-\sin(x)$ sur $[0,\pi]$.
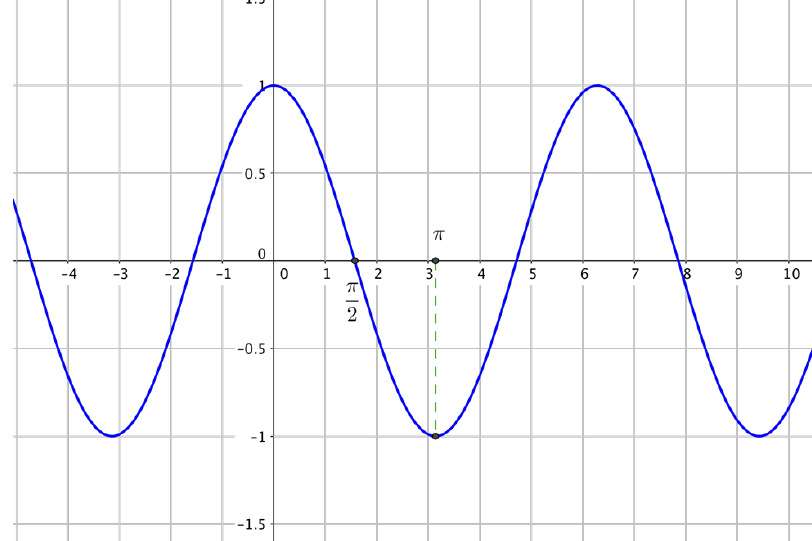
Représentation graphique
Courbe représentative de la fonction cosinus obtenue avec les propriétés de parité et de périodicité de la fonction:
Propriétés algébriques et autres formules
Pour tout $x\in\mathbb{R}$, $\cos^2(x)+\sin^2(x)=1$.
Pour tout $x\in\mathbb{R}$, $\cos(2x)=2\cos^2(x)-1$.
Pour tous $a,b$ réels, $\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)$.
Formule d’Euler : $\cos(\theta)= \dfrac{e^{i\theta}+e^{-i\theta}}{2}$, où $e^{i\theta}$ est le nombre complexe de module 1 et
d’argument $\theta$ : $e^{i\theta}=\cos ({\theta}) +i\sin({\theta})$.
$\cos(-x) =\cos(x)$
$\cos(x+\pi)= -\cos(x)$
$\cos(\frac{\pi}{2}-x)= \sin(x)$
Étude de la fonction sinus
Etude de la fonction sinus
Domaine de définition et dérivée
La fonction sinus est définie sur $\mathbb{R}$.
Elle est impaire (pour tout $x\in\mathbb{R}, \sin(-x)=-\sin(x)$) et $2\pi$-périodique (pour tout $x\in\mathbb{R}, \sin(x+2\pi)=\sin(x)$) ce qui permet de restreindre son étude à $[0,\pi]$.
Son domaine de dérivabilité est $\mathbb{R}$ et pour tout $x\in\mathbb{R}, \sin'(x)=\cos(x)$.
Variations sur $[0,\pi]$
Pour étudier les variations de la fonction sinus, on étudie le signe de sa dérivée c’est-à-dire le signe de $\cos(x)$ sur $[0,\pi]$.
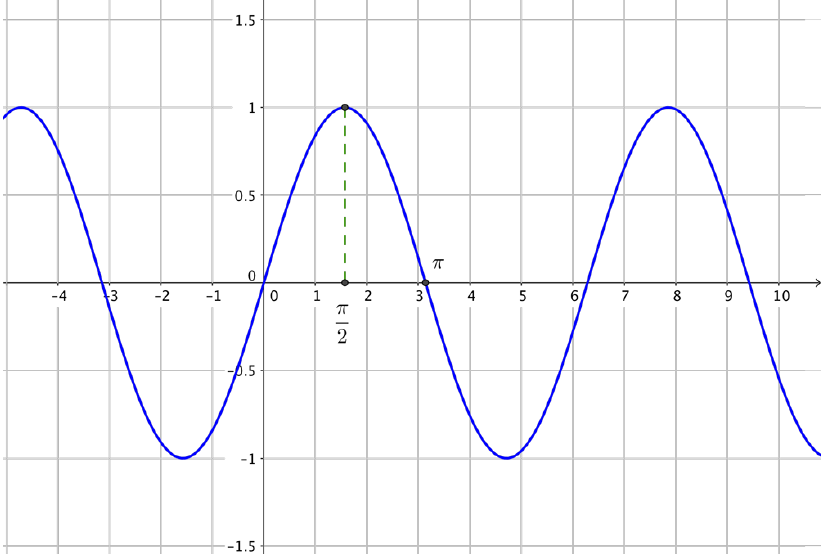
Représentation graphique
Courbe représentative de la fonction sinus obtenue avec les propriétés de parité et de périodicité de la fonction :
Propriétés algébriques et autres formules
Pour tout $x\in\mathbb{R}$, $\cos^2(x)+\sin^2(x)=1$.
Pour tout $x\in\mathbb{R}$, $\sin(2x)=2\cos(x)\sin(x)$
Pour tous $a,b$ réels, $\sin(a+b)=\cos(a)\sin(b)+\cos(b)\sin(a)$.
Formule d’Euler : $\sin(\theta)= \dfrac{e^{i\theta}-e^{-i\theta}}{2i}$.
$\sin(-x)=-\sin(x)$
$\sin(x+\pi)= -\sin(x)$
$\sin(\frac{\pi}{2}-x)= \cos(x)$
Équations trigonométriques
Equations trigonométriques
Egalité de cosinus ou de sinus
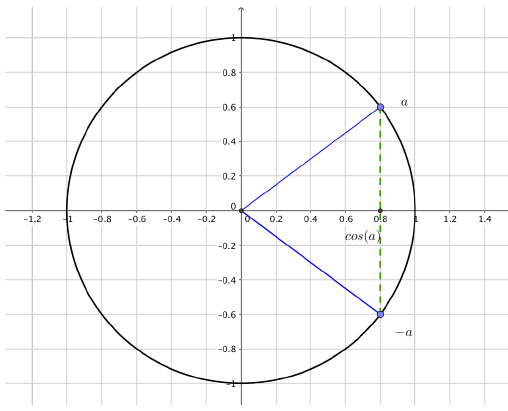
Conditions d’égalité de deux cosinus :
$ \cos(x)=\cos(a) \Leftrightarrow x=a+2k\pi \text{ ou } x=-a+2k\pi \text{ avec } k\in \mathbb{Z}$
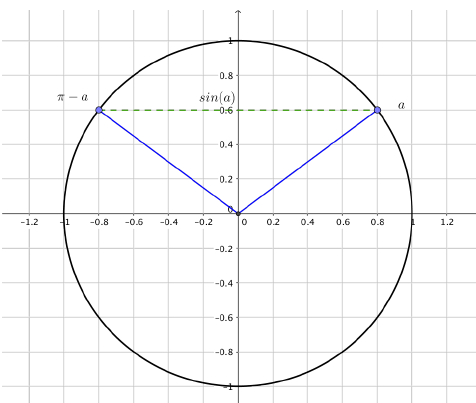
Conditions d’égalité de deux sinus :
$\sin(x)=\sin(a) \Leftrightarrow x=a+2k\pi \text{ ou } x=(\pi-a)+2k\pi \text{ avec } k\in\mathbb{Z}$
Exemple
Résoudre dans $\mathbb{R}$ l’équation $\sin(3x)=\dfrac{\sqrt2}{2}$
On a $\dfrac{\sqrt2}{2}=\sin\left( \dfrac{\pi}{4}\right)$ d’après le cours, donc :
$\sin(3x)=\dfrac{\sqrt2}{2} \Leftrightarrow 3x=\dfrac{\pi}{4}+2k\pi$ ou $3x=\left(\pi-\dfrac{\pi}{4}\right)+2k\pi = \dfrac{3\pi}{4}+2k\pi $
C’est à dire :
$x=\dfrac{\pi}{12}+\dfrac{2k\pi}{3}$ ou $x=\dfrac{\pi}{4}+\dfrac{2k\pi}{3}$ avec $k\in\mathbb{Z}$
Équations trigonométriques - Exercice
Résoudre dans \( \mathbb{R}\) les équations suivantes :
1) \(cos \ x = -\frac{\sqrt{3}}{2}\)
2) \(sin \ 3x = \frac{\sqrt{2}}{2}\)
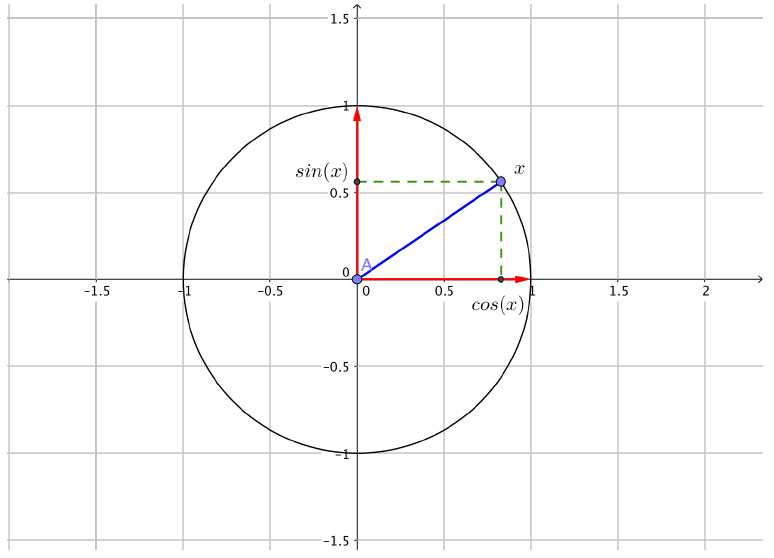
Cosinus et sinus d'un nombre réel
Cosinus et sinus d’un nombre réel
Définition
Soit $x\in\mathbb{R}$.
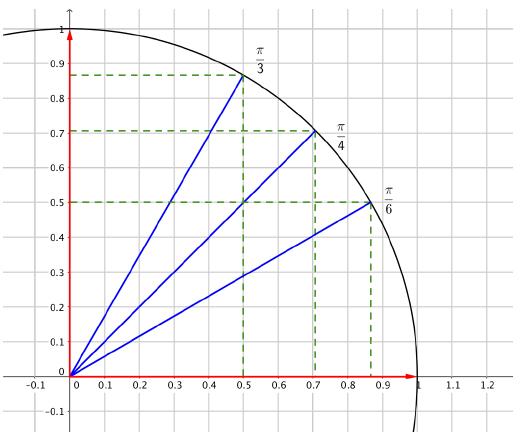
En plaçant le point $x$ sur le cercle trigonométrique, le cosinus de $x$ est l’abscisse de ce point et le sinus de $x$ est son ordonnée.
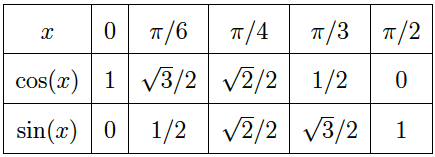
Valeurs remarquables à connaître