Chaîne de Markov - Première notion
Chaîne de Markov – Première notion
On se propose à travers un exemple d’illustrer les premières notions d’introduction aux chaînes de Markov : déterminer si une situation est une chaine de Markov, déterminer une matrice de transition et le graphe pondéré des états ainsi que la matrice de l’état initial.
Exemple :
Esope le chat n’a que trois activités chaque jour : Manger, Dormir et Jouer. Ses journées sont semblables et indépendantes. Toutes les minutes il peut soit changer d’activité soit continuer celle en cours mais sans que ses activités précédentes de la journée n’influent sur sa décision.
Quand il dort, il a 9 chances sur 10 de ne pas se réveiller la minute suivante.
Quand il se réveille, il a 1 chance sur 2 qu’il aille manger et 1 sur 2 qu’il aille jouer.
Le repas ne dure qu’une minute.
Après avoir mangé, il a 3 chances sur 10 de jouer et 7 sur 10 de dormir.
Il y a 8 chances sur 10 qu’il dorme la minute après avoir joué.
On suppose qu’Esope dorme initialement.
On souhaite former une chaine de Markov à partir de cette situation et déterminer son état initial, sa matrice de transition et son graphe pondéré.
On commence par donner l’ensemble des états possibles pour Esope le chat, en prenant les majuscules de chaque état : $E = \{M, D, J\}$.
Puisque l’activité du chat ne dépend que de la minute précédente et pas des minutes antérieures et que chaque minute est indépendante, il s’agit bien d’une chaine de Markov.
Par définition une chaine de Markov est sans mémoire, c’est à dire une chaine dont l’évolution ne dépend pas du passé mais seulement du présent.
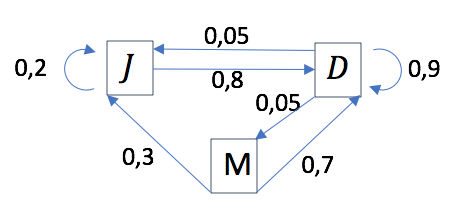
Le graphe des états fait intervenir trois sommets correspondant aux trois états. Ces sommets sont reliés par des arrêtes pondérés de la probabilité de passer d’un état à un autre la minute d’après.
Si il dort, il a 9 chances sur 10 de rendormir : on indique cela par une arrête partant de $D$ et revenant à $D$ avec une probabilité de 0,9.
Quand il se réveille, il a 1 chance sur 2 qu’il aille manger : cela correspond à une probabilité de $0,1 \times 0,5 = 0,05$ (on se souvient que dans 9 cas sur 10 il dort). On trace donc une arrête de $D$ vers $M$ avec une probabilité de $0,05$. Les flèches sur les arrêtes orientent le sens de parcours et sont donc indispensables.
Comme le repas ne dure qu’une minute, il ne peut pas remanger la minute d’après. On indique par une arrête allant de $M$ vers $J$ avec une probabilité de $0,3$ le fait qu’il a 3 chances sur 10 de jouer après mangé. De même, on indique par une arrête allant de $M$ vers $D$ avec une probabilité de $0,7$ le fait qu’il a 7 chances sur 10 de jouer après mangé.
On procède de la même manière en partant du sommet $J$.
Un moyen d’éviter les erreurs est de calculer la somme des probabilités des arrêtes sortantes d’un sommet qui doit valoir $1$.
La matrice de transition associé à la situation est notée $P$ et est de dimensions $3 \times 3$ car la chaine de Markov contient $3$ états.
Le nombre contenu à l’intersection de la ligne $i$ et de la colonne $j$ donne la probabilité de passer de l’état de la ligne $i$ à l’état de la ligne $j$.
L’ordre des états est le même pour les lignes et les colonnes et on prend ici l’ordre dans lequel on a listé les états.
$P = \left ( \begin{array}{ccc} 0,9 & 0,05 & 0,05 \\ 0,7 & 0 & 0,3 \\ 0,8 & 0 & 0,2 \end{array} \right )$
Ainsi, le nombre de la première ligne et première colonne correspond à la probabilité de passer de l’état $D$ à l’état $D$, c’est à dire $0,9$.
Le nombre de la deuxième ligne troisième colonne donne la probabilité de passer de l’état $M$ à l’état $J$ c’est à dire $0,3$.
On vérifiera après avoir complété la matrice que la somme d’une ligne vaut $1$.
L’état initial $\Pi_0$ est donné sous forme d’une matrice ligne. On suppose qu’Esope dort lorsque la journée commence. Il est donc forcément dans l’état $D$. Ainsi, $\Pi_0 = ( \begin{array}{ccc} 1 & 0 & 0 \end{array})$


