Identifier une espèce chimique
Identifier une espèce chimique
I. La chromatographie sur couche mince (CCM)
La chromatographie sur couche mince (CCM) est une méthode permettant d’identifier une espèce chimique. Cette méthode est utilisée en TP et demande du travail.
Principe
Les espèces chimiques ont des affinités différentes avec la phase fixe et la phase mobile (l’éluant).
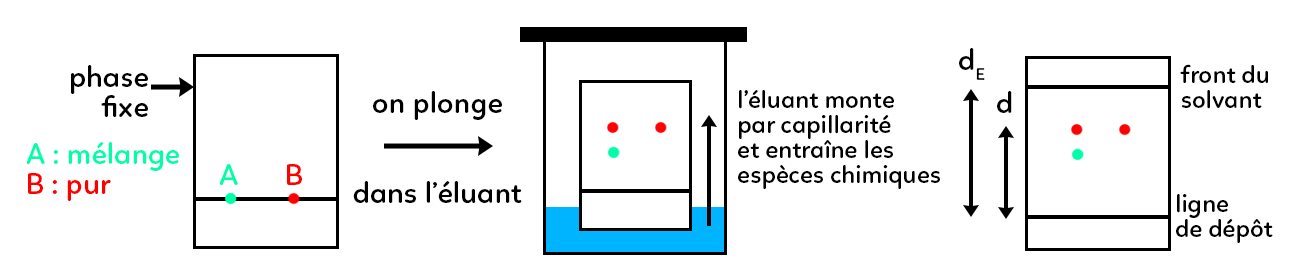
La phase fixe est le rectangle, cela peut être du papier Whatman ou une couche de silice. Pendant l’expérience cette phase ne va pas bouger. Sur cette phase fixe on dépose, au niveau de la ligne de dépôt, le mélange formé lors de la réaction ainsi que l’élément pur que l’on souhaite identifier : une goutte A et une goutte B. Ensuite la plaque est plongée dans l’éluant. L’éluant est un liquide qui va monter le long de la plaque par capillarité : c’est la phase mobile. En montant, l’éluant va entraîner les espèces chimiques contenues dans A et B. Dans cet exemple, il a 2 tâches qui sont montés de la goutte A et une tâche de la goutte B. On peut donc constater que A contenait 2 espèces chimiques différentes et B une seule (en effet, B est pur). Il faut arrêter la montée de l’éluant avant que celui-ci n’atteigne le haut de la plaque. Le front de l’éluant doit se trouver à environ 1 cm du haut de la plaque lorsque l’on stoppe celui-ci. On obtient au final la dernière figure.
Bilan
Pour chaque espèce chimique, il y a une tâche, et pour chacune de ces tâches, il existe un rapport frontal qui est caractéristique de l’espèce chimique.
Calcul du rapport frontal
On note $d$ la distance entre la tâche et la ligne de dépôt et on note $d_E$ la distance entre la ligne de dépôt et le front de l’éluant.
Le rapport frontal est : $R_f=\dfrac{d}{d_E}$
II. Les grandeurs caractéristiques d’une espèce chimique
Il existe d’autres méthodes pour identifier une espèce chimique. En effet, on peut se baser sur des grandeurs caractéristiques d’une espèce chimique :
– la température de fusion (solide $\to$ liquide). Exemple : l’eau a une température de fusion T = 0 °C, donc si un solide que l’on veut identifier fond à 0 °C, on peut en déduire que c’est de l’eau.
– la température d’ébullition (liquide $\to$ gaz). Exemple : l’eau a une température d’ébullition de 100 °C, donc si un liquide transparent bout à partir de 100 °C, alors on en déduit que c’est de l’eau.
Attention : Toutes les températures de fusion et d’ébullition sont indiquées sous une pression atmosphérique et à 20 °C.
Protocole
Pour mesurer ces grandeurs, il faut par exemple une plaque chauffante et un thermomètre pour la température d’ébullition. Pour la température de fusion on utilise un banc Kofler : c’est une plaque de métal sur laquelle la température n’est pas la même en tout point.
Les groupes caractéristiques
Les groupes caractéristiques
I. Définition
Un groupe caractéristique est une partie d’une molécule. Elle est composée d’un ou plusieurs atomes qui ne sont pas du carbone : en effet le carbone forme la structure principale des molécules et les autres atomes forment ces groupes qui sont accrochés au squelette carboné. Un groupe caractéristique est donc nécessairement relié à un atome de carbone (c’est ce qui lui permet de s’accrocher à la molécule).
II. Fonctions importantes
Il est intéressant de s’intéresser aux groupes caractéristiques car ils sont la signature d’une molécule et sa spécificité. En effet ce sont les groupes caractéristiques qui vont déterminer la réactivité d’une molécule vis à vis des autres molécules et son comportement en général (par exemple le fait qu’il soit solide, liquide ou gazeux.
Un groupe caractéristique peut aussi être appelé « fonction caractéristique » ou simplement « fonction ».
Fonction alcool
– C – OH
Fonction acide
– C = O
\( \ \ \) |
\( \) OH
Fonction cétone
– C = O
Fonction amine
– NH2
Fonction ester
– C – O –
\( \ \) ||
\( \ \) O
Concentration molaire et massique
I. La concentration molaire
Tout d’abord, la concentration molaire est égale à la quantité de matière de soluté dissous par litre de solution.
Ainsi on a la formule :
$C= \dfrac{n}{V}$
Où $C$ est la concentration molaire (en $mol.L^{-1}$), $n$ est la quantité de matière du soluté (en $mol$) et $V $est le volume dans lequel est le soluté (en L).
Exemple
On dissout $0,1mol$ de NaCl (sel) dans 2 L d’eau. La concentration molaire est donc :
$C(NaCl)=[NaCl]=\dfrac{n(NaCl)}{V_{solution}}=\dfrac{0,1}{2}=0,05 mol.L^{-1}$
II. Relation entre la concentration molaire et la concentration massique
La concentration massique et la concentration molaire sont reliés par cette relation : $C_m=C \times M$
Où $C_m$ est la concentration massique, $C$ la concentration molaire et $ M$ la masse molaire du soluté.
Démonstration
On a $C=\dfrac{n}{V}$ et $n=\dfrac{m}{M}$
Ainsi, si on injecte l’équation de $n,$ on a $C= \dfrac{m}{M \times V}$
On a alors $C_m=\dfrac{m}{V}$
Ainsi, $C = \dfrac{C_m}{M}$
D’où $C_m = C \times M$
Cette équation est bien homogène en unité car $C_m$ est en $g/L$ et $C \times M $ a pour unité $\dfrac{mol}{L} \times \dfrac{g}{mol}=g/L$


