Variation d’énergie interne d’un système : définitions, formule, calcul ΔU
Le système thermodynamique
Ce cours du chapitre L’énergie : conversions et transferts traite du système en thermodynamique et de l’énergie interne U. Il t’explique ce qu’est un système et quels en sont les différents types (système ouvert, système fermé, système isolé), mais aussi ce qu’est l’énergie interne, comment elle varie et comment calculer ΔU.
Le système thermodynamique : ce que tu vas réviser
I. Définition d’un système
Système : un corps ou un ensemble de corps qui est l’objet de notre étude, de l’exercice. Parfois, on note Σ le système.
II. Exemple concret d’un système
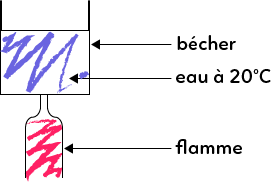
Imaginons que nous avons une flamme qui vient chauffer de l’eau qui se trouve dans un bécher. Le support du bécher et de la flamme ne sont pas représentés ici car c’est purement schématique.
Il y a plusieurs possibilités :
|
Système |
eau |
eau + bécher |
eau + bécher + flamme |
|
échange d’énergie |
reçoit de l’énergie termique ΔU>O |
reçoit de l’énergie termique ΔU>O |
ne reçoit pas d’énergie termique ΔU=O |
On peut soit considérer que le système est uniquement l’eau ou alors l’eau plus le bécher ou alors l’eau plus le bécher plus la flamme. C’est extrêmement important de faire ce choix là dès le début de l’exercice parce que, de cela dépend tout le traitement de l’exercice.
Voici un exemple : si on se pose la question s’il y a échange d’énergie. Est-ce qu’il y a de l’énergie qui arrive ou qui part du système ?
Si le système est l’eau, très clairement, l’eau reçoit de l’énergie car le bécher est réchauffé grâce à l’action de la flamme.
Si le système est l’eau + bécher, les deux vont se faire réchauffer par la flamme donc le système eau + bécher reçoit de l’énergie, sa température va monter.
Et, si le système c’est l’eau + bécher + flamme, est-ce qu’il y a de l’énergie qui vient de l’extérieur ? Non !
Alors, on peut dire qu’il y a un échange énergétique avec le gaz qui se trouve dans la pièce, mais on fait abstraction de cet échange possible. Il n’y a pas d’énergie qui provient de la flamme car la flamme fait elle-même partie du système. Si on raisonne en termes d’énergie interne, l’énergie interne du premier et du second système augmente puisque l’énergie augmente (ΔU>0). Mais, l’énergie interne de ce troisième système, qui ne subit aucune source de chaleur extérieure, est constante : ΔU=0.
C’est donc extrêmement important de bien déterminer le système dès le départ.
III. Les différents types de systèmes
Mots de vocabulaire sur le système qu’il faut absolument connaître ainsi que leur signification :
A. Le système ouvert
Un système qui est ouvert peut vouloir dire qu’il peut échanger de l’énergie avec l’extérieur (pas obligatoire) : énergie thermique (quantité de chaleur), mécanique (travail), électrique (générateur par exemple) ou chimique (réactions exothermiques). Un système ouvert peut aussi échanger de la matière car il est justement ouvert. Sa quantité de matière reçue peut augmenter ou diminuer. Par exemple, un gaz dans une tuyère d’avion. À chaque instant il y a de l’injection de gaz qui a lieu, et à chaque instant il y a des échanges énergétiques car il y a de la combustion, décompression, etc.
B. Le système fermé
Celui-ci ne peut qu’échanger de l’énergie, mais ça n’est pas une obligation. Par exemple, à l’intérieur d’une cocotte-minute fermée hermétique, les parois sont solides et ne peuvent pas bouger. Il ne peut pas y avoir de l’eau qui rentre ou de l’eau qui sort. On fait l’hypothèse que la cocotte-minute soit vraiment fermée hermétiquement avec le bouchon scotché, qui ne bouge pas. C’est un système fermé, donc, car la seule chose qui peut lui arriver c’est recevoir de l’énergie de l’extérieur, par la conduction thermique par la partie métallique de la cocotte-minute. En aucun cas il n’y aura échange de matière.
C. Le système isolé
On parle de système isolé dans le cas où le système ne peut ni recevoir ni échanger de la matière. Pas d’échanges avec l’extérieur ! Par exemple, à l’intérieur des parois solides et calorifugées. C’est un exemple qui revient souvent dans les exercices. « Calorifugé » signifie qu’il n’y a pas d’échange de chaleur, pas d’échange thermique. Pas d’échange mécanique et si les parois sont fermées, il n’y a pas d’échange de matière.
Pour aller plus loin dans L’énergie : conversions et transferts
Après avoir étudié ce cours, nous te conseillons de poursuivre avec ces autres notions :
L'énergie interne U
L’énergie interne U : ce que tu vas réviser
I. Définition de l’énergie interne
Comment calculer la variation d’énergie interne ?
L’énergie interne d’un système représente l’ensemble de toutes les énergies qui se manifestent à l’échelle microscopique : l’énergie cinétique des particules, les énergies d’interaction, etc. Pour calculer la variation de l’énergie interne entre deux instants, il faut connaître sa formule notée $ΔU$. $ΔU= U2-U1$ ou $U(final)-U(initial)$.
II. Calcul de ΔU
Comment calculer l’énergie interne ?
Pour calculer ΔU, il faut connaître cette formule. On doit savoir que : $ ΔU = m\times c\times (T_f-T_i)$
avec $m$ la masse du système, $c$ la capacité thermique du système, $T$ les températures.
$(T_f-T_i)$ correspond bien à une variation de température, donc, tout comme on avait noté $ΔU$ pour parler de la variation de l’énergie interne d’un système on peut utiliser $ΔT$ pour parler de la variation de température.
Donc la variation de l’énergie interne est proportionnelle à la variation de température : $ΔU = m\times c\times (T_f-T_i) = m\times c\times ΔT$.
Concernant les unités, la variation de l’énergie interne est en Joules (J), la masse est en kilogrammes (kg), la capacité thermique est en J.kg-1.K-1 (on l’appelle parfois d’ailleurs capacité thermique massique), les températures sont en Kelvin (K) mais le delta de température peut être aussi exprimé en degrés Celsius car ce n’est pas la valeur absolue des températures mais l’écart entre celles-ci. Il est le même peu importe l’unité utilisée.
Première remarque : le système doit être un corps pur. En fait, la valeur de la capacité thermique change en fonction des matériaux : eau, béton, verre, etc. À chaque corps pur correspond une capacité thermique. Si, par exemple, dans un système donné, on se retrouve avec un mélange de deux matériaux complètement différents, on ne peut pas calculer $ΔU$ sinon on ne pourra pas choisir de valeur pour $c$.
Dans ces cas-là, il faut décomposer le système en deux sous-systèmes et calculer séparément la variation d’énergie interne de chacun des sous-systèmes. Ce qui compte quand on applique cette formule c’est que ça s’applique à un bloc. Le corps est pur, rien n’empêche d’additionner les $ΔU$ des différents sous-systèmes pour avoir le $ΔU$ total.
Deuxième remarque : concernant le signe de $ΔU$. Si on se fie à la formule, si la température augmente, la différence $T_f-T_i$ est positive, la masse est toujours positive ainsi que la capacité thermique donc $ΔU$ est positif. Cela veut dire que l’énergie interne augmente. Est-ce logique ?
Oui, car si la température augmente, l’agitation microscopique des molécules augmente elle aussi. La température correspond à l’agitation des molécules. Si l’agitation augmente, l’énergie cinétique des molécules augmente. Justement, dans la définition on dit que l’énergie interne est l’énergie cinétique des particules élémentaires. Si l’énergie cinétique augmente, $U$ augmente et donc $ΔU$ est positif.
Troisième remarque : par contre si la température diminue, on a l’inverse : la température diminue, l’énergie microscopique diminue, donc $U$ diminue et $ΔU$ est négatif.
III. Exemple concret de l’énergie interne
On part d’un réfrigérateur qui permet à 2,0 kg de viande de passer de 20 °C à 4 °C. Quelle énergie est absorbée par le réfrigérateur ?
On raisonne sur le système étant la viande. On considère que la viande c’est de l’eau. Et on calcule la variation de son énergie interne :
$ΔU = m\times c\times ΔT$
$ΔU = -2\times 4185\times 16$
$ΔU = -130kJ$
On remarque que l’on a un signe « – » donc cela veut dire que le système a perdu de l’énergie. Comment l’interprète-t-on ? Ce système « viande » a perdu de l’énergie et l’énergie perdue a été absorbée par le réfrigérateur. Pour répondre à la question « quelle énergie est absorbée par le réfrigérateur ? », on peut dire que le réfrigérateur a absorbé 130 kJ.
Pour aller plus loin dans L’énergie : conversions et transferts
Après avoir étudié ce cours, nous te conseillons de poursuivre avec ces autres notions :


