Flux thermique : système en contact avec un thermostat
I. Flux thermique
Rappel : lorsqu’on a une température à l’extérieur d’une zone notée T1 et une température T2 à intérieur de la zone, si T1>T2, alors on a un flux thermique de la zone chaude vers la zone froide. C’est un transfert d’énergie thermique (en Joule).
Le flux thermique $\phi$ : $\phi = \dfrac{Q}{\Delta t}$, avec $Q$ la quantité de chaleur échangé sur une durée $\Delta t$.
Si on a 10J échangé pendant 5secondes, on aura un flux thermique de 2J.s-1. On peut avoir par exemple 30J.s-1.
II. Cas du thermostat
C’est un système à température constante. Si la zone T1 est à température constante, on dira que la zone est un thermostat. La zone intérieure sera le système et on dira que le système est entouré d’un thermostat.
On a un rectangle avec une température $T$ et autour une zone à température $T_{ext}.$ En supposant que la température extérieure est plus grande, on aura un flux thermique de l’extérieur vers l’intérieur. Il existe une formule qui permet de mesurer le flux entre le thermostat et le système :
$\phi = h\times S \times (T_{paroi} – T)$ (on suppose que la paroi est à même température que la température du thermostat).
$h$ est le coefficient de Newton. On a un flux proportionnel à une température. On peut retrouver les unités facilement dans la formule.
III. Remarque : lien entre coefficient de Newton et résistance thermique
On a vu que $\phi = \dfrac{Text-T}{Rth}$.
On vient de voir que dans le cas du thermostat $\phi = h\times S \times (T_{paroi} – T)$
Donc on a : $\phi = \dfrac{Text-T}{Rth} = h\times S \times (T_{paroi} – T)$.
D’où $\dfrac{Text-T}{Rth} = h\times S \times (T_{paroi} – T)$.
Donc : $\dfrac{1}{Rth} = h\times S$.
La première formule $\phi = \dfrac{Text-T}{Rth}$ n’est pas spécifique du thermostat elle est générale. La dernière formule trouvée peut être très utile dans les exercices. On se sert toujours d’hypothèse par rapport au flux thermique. On suppose toujours que la température extérieure est plus chaude que celle de l’intérieur. Mais que se passe-t-il si c’est l’inverse ?
Aucun problème, puisqu’on se sert de convention. On se place dans le cas où le flux est positif. Si on a l’inverse, la différence de température est négative et le flux aussi. Le flux est donc dans le sens inverse. Il faudra s’adapter avec le signe pour connaître le sens du flux.
Flux thermique, résistance thermique
I. Flux thermique
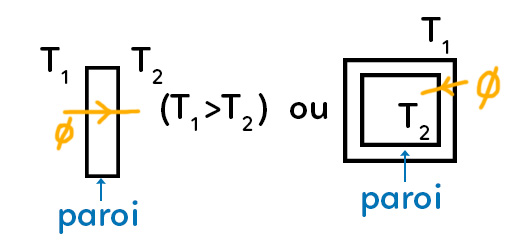
Il y a un transfert d’énergie d’une zone à une autre. Pourquoi ?
Imaginons le cas où une paroi (un mur par exemple) sépare deux pièces. De part et d’autre du mur, on n'a pas la même température : T1 d’un côté et T2 de l’autre. On admet que T1>T2. Il va y avoir un flux thermique qui va de la zone chaude vers la zone froide. Ce flux thermique est noté $\phi$.
On peut s’imaginer aussi une zone intérieure à la température T2 et une zone extérieure à la température T1 avec des parois qui renferment cette zone centrale à la température T2. De même on aura un flux $\phi$ qui va de la zone chaude vers la zone froide. Pendant une durée $\Delta t$, il va y avoir une quantité de chaleur $Q$ transférée de la zone chaude vers la zone froide.
$\phi = \dfrac{Q}{\Delta t}$.
$Q$ est une quantité de chaleur transférée en Joules, $\Delta t$ est en secondes et $\phi$ en Watts.
II. Lien entre flux thermique et résistance thermique.
Le flux thermique est proportionnel à la différence de température entre les deux compartiments : $\phi = k \times (T1-T2)$.
C’est la différence de température qui créé le flux thermique. Si les deux compartiments étaient à la même température, il n’y aurait pas d’échange. Plus la différence est importante plus le flux thermique est important. Au lieu d’écrire $k$ le coefficient de proportionnalité, on va écrire $\dfrac{1}{R_{th}}$.
C’est donc $R_{th}$ la résistance thermique.
On a alors : $\phi = \dfrac{T1-T2}{R_{th}}$.
Les températures sont en Kelvin, $\phi$ en Watts et la résistance thermique $R_{th}$ en K.W-1.
Le coefficient de proportionnalité est égal à : $\dfrac{1}{Rth}$.
Remarque :
En électricité, pour un conducteur ohmique, on a $I = \dfrac{U}{R}$. Il y a donc une similitude entre ces deux équations. $I$ en électricité correspond au transfert d’électrons, des charges. $\phi$ est le transport d’énergie. $U $ est la différence de potentiel de part et d’autre du résistor et $T1-T2$ la différence de température de part et d’autre de la paroi. On a donc appelé la résistance thermique par analogie à la résistance thermique.
Attention, dans les exercices on donne parfois la résistance thermique surfacique $r_{th}$.
On aura alors : $r_{th} = R_{th}\times S$, avec $R_{th}$ en K.W-1, $r_{th}$ en K.W-1.m-2 et la surface S en m2.
Cette formule est un vrai piège. Ce qu’on appelle une quantité surfacique, on le divise par la surface. Si on ne fait pas attention, on peut se dire que la résistance thermique surfacique est la même chose que résistance divisée par la surface. Ici c’est la résistance thermique multipliée par la surface.
Reprenons le flux thermique $\phi = \dfrac{T1-T2}{R_{th}}$.
Le « vrai » flux surfacique, celui par unité de surface s’écrit comme ceci : $\dfrac{\phi}{S} = \dfrac{T1-T2}{S\times R_{th}} = \dfrac{T1-T2}{r_{th}}$.
Donc, rth est liée au flux surfacique. On retrouve finalement la formule : $r_{th} = R_{th}\times S$.
Si l’exercice ne donne pas la résistance thermique surfacique mais la conductivité thermique $\lambda$, on peut retrouver la résistance thermique grâce à la formule suivante : $R_{th} = \dfrac{e}{\lambda \times S}$. L’épaisseur $e$ est en mètres, la surface de la paroi en m2 et la conductivité $t$ hermique en W.m-1.K-1. On peut ensuite, par exemple, calculer le flux thermique.


