Les référentiels galiléens
En Physique, les exercices commencent souvent par cette phrase : « On considère le référentiel terrestre comme galiléen » ou alors par la question « Ce référentiel est-il galiléen ? ». En effet, toutes les lois mécaniques vues au lycée ne fonctionnent que dans les référentiels galiléens.
I. Définition théorique mais peu exploitable
Un référentiel galiléen est un référentiel où le principe d’inertie est vérifié. On dit parfois aussi un référentiel inertiel.
Rappel : si sur un objet, il y a soit des forces extérieures qui se compensent (vecteur nul), soit pas de forces qui s’exercent sur cet objet, alors cet objet sera soit en mouvement rectiligne uniforme (MRU) soit immobile. La réciproque est vraie. Le référentiel est galiléen s’il remplit ces conditions.
II. Autre définition
Un référentiel est galiléen s’il est en translation rectiligne uniforme par rapport à un autre référentiel galiléen.
III. Quelques exemples courants
A. Référentiel terrestre
Le référentiel terrestre est très apprécié car il permet d’étudier facilement les mouvements. Il suffit d’être posé sur Terre et de regarder un objet se mouvoir pour être dans le référentiel terrestre. Est-il galiléen ?
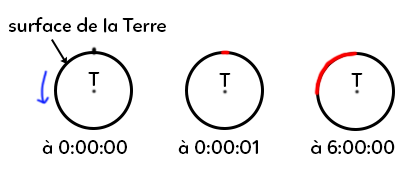
$T$ est le centre de la Terre, le cercle noir autour est la surface de la Terre. On va donc regarder ce qu’il se passe au niveau de sa surface. On a placé un observateur qui présente des positions différentes en fonction des heures (minuit, minuit et une seconde, 6 h. La trajectoire en rouge à minuit et une seconde représente un petit trait. C’est un segment. Il est donc bien en mouvement rectiligne uniforme. Par contre, si on regarde la trajectoire à 6 h, c’est un arc de cercle. On est donc plus dans la définition car le référentiel terrestre n’a pas eu un mouvement de trajectoire rectiligne uniforme. Donc, sur une longue période le référentiel terrestre n’est pas galiléen. Par contre, sur une toute petite durée, le référentiel terrestre est galiléen. Qu’est-ce qu’une petite durée ? C’est une petite durée comparée à 24 h, quelques secondes par exemple.
B. Référentiel géocentrique
C’est un référentiel donc le centre est le centre de la Terre, et les axes pointent vers les étoiles lointaines.
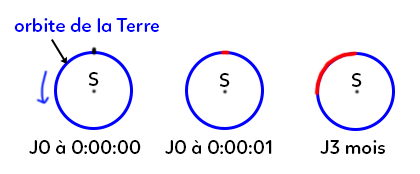
Ici, on va suivre le centre de la Terre au cours du temps. La Terre tourne autour du Soleil S et en bleu on a l’orbite de la Terre (trajectoire de la Terre autour du Soleil). La Terre présente des positions différentes selon les heures : minuit à J0, minuit et une seconde à J0 et J = 3 mois. A minuit et une seconde, la Terre a bougé si peu qu’on peut considérer sa trajectoire comme rectiligne. Si la durée est courte, le référentiel géocentrique est galiléen. Par contre, au bout de 3 mois, la trajectoire de la Terre est un arc de cercle, n’est pas rectiligne et donc le référentiel n’est pas galiléen. On peut imaginer que l’on regarde la situation du point de vue du référentiel héliocentrique, qui est un meilleur référentiel galiléen.
C. Référentiel de Copernic
C’est un meilleur référentiel galiléen que les deux autres car le référentiel est le centre du système solaire et donc son mouvement va être très faible. Le système solaire a un mouvement elliptique mais son rayon est si énorme que la trajectoire n’est qu’une droite. C’est pour cela que c’est un très bon référentiel galiléen, meilleur que le référentiel terrestre ou géocentrique.
La deuxième loi de Newton
Cette deuxième loi de Newton est le point de départ pour résoudre un problème de mécanique : par exemple lorsqu’il s’agit de trouver la trajectoire d’un mobile en considérant les forces qu’il subit.
I. La deuxième loi de Newton
Il faut être dans un référentiel galiléen pour pouvoir l’utiliser. Il faut donc le préciser au début.
La loi dit que : $\sum_{\overrightarrow{F}_{ext}} = \dfrac{d\overrightarrow{p}}{dt}$.
$\overrightarrow{p}$ est la quantité de mouvement et vaut $\overrightarrow{p} = m\times \overrightarrow{v_G}$.
La masse du système est en kilogrammes, la vitesse du centre de masse du système est en $m.s^{-1}$ et la somme des forces extérieures qui s’appliquent est en Newton. Il existe deux cas particuliers :
– Si la masse est constante : c’est le cas de la plupart des cas. En effet, une balle possède toujours la même masse. Par contre, la fusée est un objet dont la masse varie car elle décolle avec des réserves pour sa propulsion et les réserves sont brûlées et éjectées sous forme de gaz. La masse de la fusée varie donc au cours du temps. Dans ce cas, si la masse est une constante elle sort de la dérivée et on a juste la dérivée de la vitesse.
$\sum_{\overrightarrow{F}_{ext}} = m\times \dfrac{d\overrightarrow{v}}{dt} = m\times \overrightarrow{a_G}$.
– Si le système est juste un point : dans ce cas, le centre de masse est ce point.
On a alors : $\sum_{\overrightarrow{F}_{ext}} = m\times \dfrac{d\overrightarrow{v}}{dt} = m\times \overrightarrow{a}$.
II. Centre de masse
Le centre de masse est le barycentre des masses. C’est le point d’équilibre des masses.
Attention ! Si le champ de pesanteur est uniforme, c’est aussi le centre de gravité. Si le champ de pesanteur n’est pas uniforme, le centre de masse est le centre de la masse mais le centre de gravité est le centre du poids et donc ne sera pas identique. Dans les exercices cette année, le champ de pesanteur sera uniforme.
Le centre de masse est aussi le centre inertiel ou centre d’inertie. On le note $G$ est on a : $m_{tot} \times \overrightarrow{OG} = \sum_i {m_i} \times \overrightarrow{OM_i}$.
$O$ étant le centre d’un repère, $G$ le centre de masse et $m_i$ la masse du $ième$ point et $\overrightarrow{OM_i}$ la position de ce $ième$ point qui constitue le système.
Exemple simple : un système composé de deux points $M1$ et $M2.$ Dans la somme précédente, $i$ vaut $1$ puis $2.$ On place un point $O$ centre d’un repère et on applique la formule.
On a : $\sum {m} \times \overrightarrow{OG} = m\overrightarrow{OM1} + m\overrightarrow{OM2}$. $\sum {m( \overrightarrow{OM1}+\overrightarrow{M1G})} = m\overrightarrow{OM1} + m\overrightarrow{OM2}$. $\sum{\overrightarrow{M1G}} = -m\overrightarrow{OM1}+m\overrightarrow{OM2} = m\overrightarrow{M1M2}$. $\overrightarrow{M1G} = \dfrac{\overrightarrow{M1M2}}{2}$.
A titre d’entrainement, on peut poser un point $M1$ de masse $2m$ à droite d’une barre et à gauche un point $M2 $de masse $m.$ On peut ensuite montrer que le point $G$ est à un tiers de la distance $M1M2.$
III. Exemple
A. La chute libre
Notre système est une balle de centre $M$ sur un repère $(O ;x ;y).$ Le mouvement est plan donc on n’a pas besoin d’axe $z.$
$\overrightarrow{g}$ est le vecteur de pesanteur, qui est vers le bas. Que vaut $\overrightarrow{a}$ ?
Dans un référentiel galiléen, $\sum_{F_{ext}} = m\times \overrightarrow{a(M)}$. $M$ est le centre de la balle donc le centre de masse.
On va d’abord faire le bilan des forces : on a le poids et la force de frottement de l’air (comme la balle est en train de tomber) que l’on va négliger. Donc on a $\sum_{F_{ext}} = \overrightarrow{P} = m\times \overrightarrow{g} = m\times \overrightarrow{a(M)}$.
On peut simplifier les masses qui sont les mêmes et on a alors : $\overrightarrow{a} = \overrightarrow{g}$. Le vecteur accélération est placé en $ax$ et $ay.$ Et le vecteur de pesanteur est purement vertical donc a pour coordonnées en abscisses $0$ et en ordonnées $-g$ (avec $g = 9,81 m.s^{-2}$ à Paris).
Une fois qu’on a l’accélération, on peut avoir la vitesse et la position. On peut déterminer la trajectoire de cette balle qui va tomber. La vitesse est la primitive de l’accélération car l’accélération est la dérivée de la vitesse. De même on peut trouver la position en ayant la primitive de la vitesse.
B. Un bateau
On suppose que le mouvement est rectiligne uniforme. Que valent les forces qui s’exercent sur ce bateau ?
On a un bateau à voiles qui navigue sur l’eau à l’horizontale. Le poids s’applique sur le centre de gravité, vers le bas. Il y a aussi la poussée d’Archimède, vers le haut. La force de traction s’applique vers la droite au niveau des voiles. L’eau exerce un frottement sur la coque du bateau et se trouve vers la gauche.
Si la vitesse est constante, l’accélération qui est la dérivée de la vitesse vaut zéro. Dans le référentiel galiléen, on a dit que $\sum_{\overrightarrow{F_{ext}}} = m\overrightarrow{a}$.
D’où $\sum_{\overrightarrow{F_{ext}}} = \overrightarrow{0}$.
Donc, la poussée d’Archimède est compensée par le poids (même sens). Les forces de traction et de frottements se compensent également. Cela nous rappelle le principe d’inertie ! Le principe d’inertie est un cas particulier de la deuxième loi de Newton.


