Sections de solides par des plans
Sections de solides par des plans
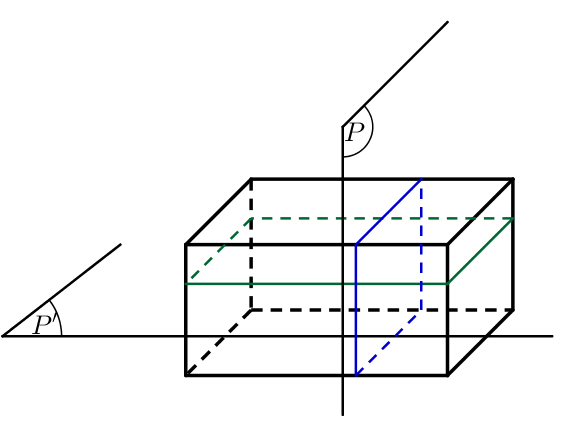
Section d’un pavé par un plan parallèle à l’une des faces :
On ne considère que des plans parallèles aux faces. Les traits pleins correspondent à des arrêtes visibles, les traits en pointillés sont des arrêtes cachées.
La section du pavé par un plan parallèle à la face de droite donne un rectangle, de même dimension que le rectangle de la face de droite.
La section du pavé par un plan parallèle à la face supérieure donne un rectangle, de même dimension que le rectangle de la face supérieure.
Section d’une sphère :
Une sphère est l’ensemble des points qui sont à égale distance du centre.
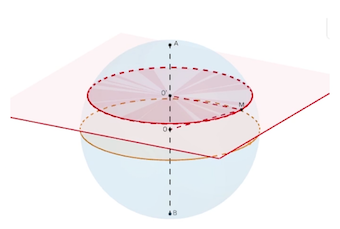
On considère la section par un plan, on obtient un disque de rayon plus petit que celui de la sphère. On peut observer ce phénomène lorsque l’on coupe une orange par exemple.
Lorsque le plan contient le centre $O$ de la sphère, la section est alors le grand disque. Pour la Terre, il s’agira de l’équateur.
Exemples de sections de solides par des plans
Exemples de sections de solides par des plans
Cette fiche de cours est un complément au programme de géométrie dans l’espace. Toutes les notions ne sont pas exigibles pour les élèves.
Définition
Une section est la figure plane que l’on obtient après avoir coupé un solide par un plan.
Lorsque l’on coupe une orange par exemple, on obtient un disque.
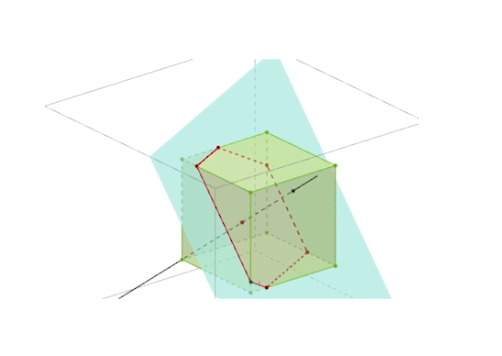
La section d’un cube par un plan parallèle à une des faces est un carré ayant les mêmes dimensions que les faces latérales.
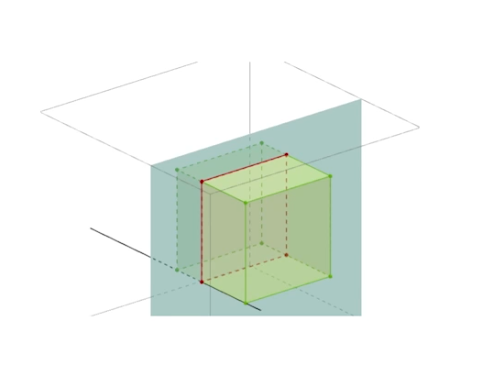
La section d’un cube par un plan quelconque, hors programme, est un polygone quelconque et parfois un triangle.
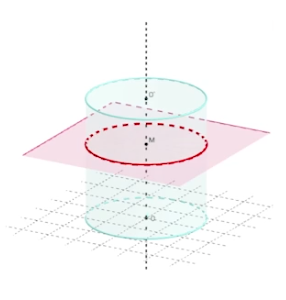
La section d’un cylindre par un plan parallèle aux bases est un disque superposable aux bases.
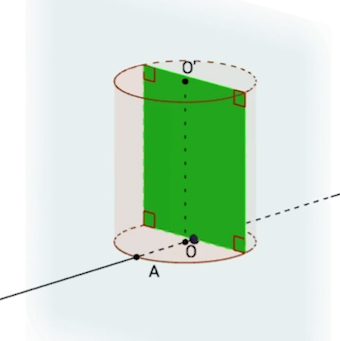
La section d’un cylindre par un plan parallèle à l’axe du cylindre, la droite $(OO’)$, est un rectangle.
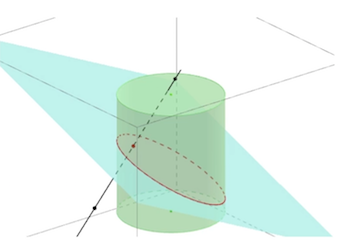
La section d’un cylindre par un plan quelconque, hors programme, peut être une ellipse.
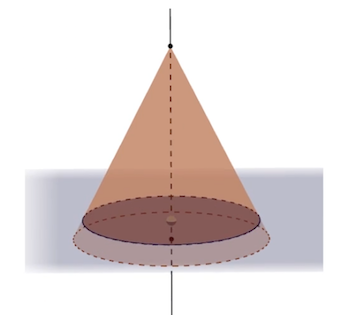
La section d’un cône par un plan parallèle à la base est un disque dont le rayon est variable selon la position du plan.
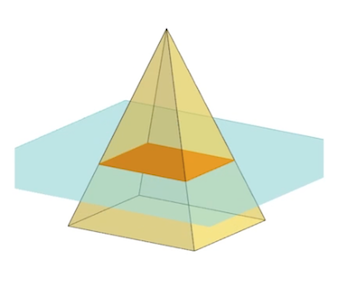
La section d’une pyramide à base rectangulaire par un plan parallèle à la base est un rectangle dont les dimensions sont proportionnelles à la base mais varient selon la position du plan.
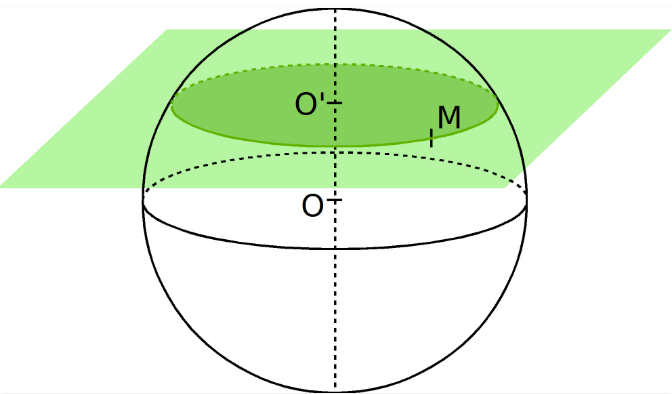
La section d’une sphère par un plan est un disque de dimension variable. Lorsque le plan contient le centre de la sphère, la section est appelée le grand disque. En se plaçant dans le triangle ${OO}’M$, on peut trouver en appliquant le théorème de pythagore la longueur $O’M$ qui est le rayon du petit disque.