Transformation chimique
On a représenté trois schémas avec : le triangle pour l’entité microscopique qui est contenue dans l’eau, le rond pour l’entité microscopique qui est comprise dans le sucre. A quoi correspondent ces trois transformations ?

Dans la première transformation, on a des entités disposées de manière organisée à gauche et désorganisée à droite, mais les entités n’ont pas changé entre le début et la fin de la transformation. Il s’agit d’une transformation physique qui est la fusion de l’eau par exemple.
Dans la deuxième transformation, on a le sucre à l’état solide ajouté dans de l’eau. On remarque qu’après la transformation, on a un mélange de sucre et d’eau qui est obtenu, mais les entités microscopiques n’ont pas été modifiées entre le début et la fin de la transformation.
Dans la troisième transformation, on a le cas d’une transformation chimique. Le mélange évolue pour donner de nouvelles entités qui n’étaient pas présentes au début. C’est une transformation chimique qui peut se détecter par l’apparition d’un solide, la disparition d’un solide, un dégagement gazeux, un changement de couleur, etc. Il y a différentes façons d’identifier une transformation chimique.
Une transformation chimique peut être écrite avec une équation de la réaction chimique. Les réactifs sont les espèces présentes avant la transformation chimique et les produits les espèces présentes après la transformation chimique. L’équation de la réaction chimique s’écrit de la manière suivante :
réactifs (+) → produits (+).
Exemple : la combustion du carbone
Les réactifs de la combustion du carbone (quand le carbone brûle) sont le carbone et le dioxygène. Le produit est le dioxyde de carbone. L’équation de la réaction chimique s’écrit, en toutes lettres, de la manière suivante : carbone + dioxygène → dioxyde de carbone.
On peut aussi écrire cette équation de la réaction chimique avec les formules chimiques des réactifs et des produits. Dans le cas du carbone, la formule chimique est C. Le dioxygène a pour formule O2 et le dioxyde de carbone CO2. On remarque dans cette équation chimique, et c’est le cas pour toutes les équations de réactions chimiques, qu’il y a le même nombre de carbone dans les réactifs et pour les produits. On remarque qu’il y a le même nombre d’oxygène dans les réactifs et dans les produits. On dit que, pendant une transformation chimique, les atomes se conservent.
Atomes et ions
Atomes et ions
La matière est constituée de tous petits grains de matière appelés les atomes.
I. Atomes
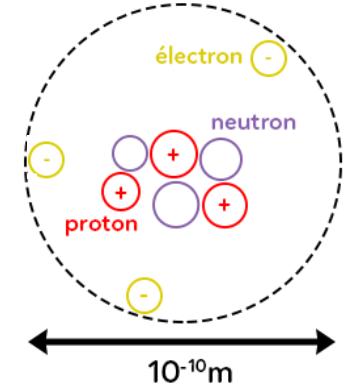
Les atomes sont eux-mêmes constitués d’un noyau, constitué de protons, chargés positivement, et de neutrons de charge nulle. Autour de ce noyau sont en mouvement des électrons, chargés négativement. La frontière de l’atome est ici représentée en pointillés et pour les dimensions de l’atome, on a environ un ordre de grandeur de 10-10 m. Ce sont des objets de très petites tailles.
Comment passe-t-on des atomes aux ions ?
II. Ions
Un ion est un atome qui a gagné ou perdu des électrons.
Exemple de l’atome de fluor
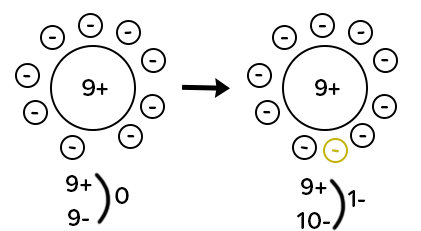
L’atome de fluor est représenté avec neuf charges positives dans son noyau (neuf protons), et neuf électrons en mouvement autour du noyau. Au niveau de la charge, on a neuf charges positives, neuf charges négatives donc on a une charge globale égale à zéro puisque tous les « plus » s’annulent avec les « moins ». C’est le cas de tous les atomes : ils sont dits électriquement neutres.
Si maintenant le fluor gagne un électron, on a un électron excédentaire. Donc on obtient neuf charges positives dans le noyau et dix charges positives autour du noyau. Il y a une charge négative excédentaire. On note l’ion qui a été obtenu : F– (la charge négative excédentaire notée en exposant). Les ions chargés négativement sont appelés les anions. Pour passer d’un atome à un anion, il faut gagner des électrons.
Exemple de l’atome de béryllium
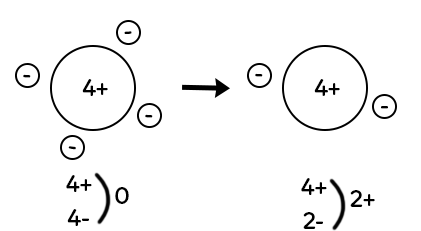
L’atome de béryllium a quatre charges positives dans son noyau et quatre électrons autour du noyau (quatre charges négatives). L’atome de béryllium, comme tous les atomes est électriquement neutre.
Si on enlève deux électrons, il ne reste plus que deux électrons autour du noyau de l’atome de béryllium. On a quatre charges positives dans le noyau et deux charges négatives autour du noyau, ce qui donne deux charges positives excédentaires. On note cet ion : Be2+ (deux charges plus excédentaires notées en exposant). Pour passer d’un atome à un ion chargé positivement, il faut une perte d’électrons. Les ions chargés positivement sont eux appelés cations.
Atomes et molécules
Atomes et molécules
Dans ce cours, nous étudions la notion d’atome et de molécule et les représentations des atomes et des molécules courantes. La matière est constituée de petits grains de matière appelés les atomes.
I. Atomes
Il existe une centaine d’atomes différents et chaque atome porte un nom, a un symbole et un modèle moléculaire. Il faut connaître le symbole et le modèle moléculaire des quatre atomes les plus courants :
Hydrogène
Son symbole est H, qui correspond à la première lettre de son nom. Son modèle est une sphère blanche.
Carbone
Son symbole est C, la première lettre de son nom. Son modèle est une sphère noire.
Oxygène
Son symbole est O, la première lettre de son nom. Son modèle est une sphère rouge.
Azote
Son symbole est N, c’est le seul pour lequel son symbole ne correspond pas à la première lettre de son nom. Son modèle est une sphère bleue.
II. Molécules
Une molécule est un ensemble d’atomes liés entre eux. Voyons le modèle des molécules, et comment, à partir du modèle, établir la formule chimique des molécules.
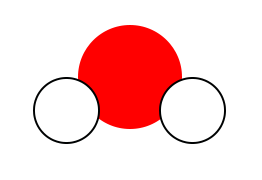
Le premier modèle est la molécule d’eau. On constate qu’elle a un atome d’oxygène et deux atomes d’hydrogène. Pour la formule, on va donc écrire le symbole des deux atomes présents : HO (par ordre alphabétique). On a deux hydrogènes donc on va préciser en indice, en bas à droite du H, le chiffre 2. On a qu’un seul atome d’oxygène : on ne l’écrit pas en indice car c’est sous-entendu qu’il n’y a qu’un seul atome. Molécule d’eau = H2O
Le deuxième modèle est celui du méthane. On a la formule et on va représenter le modèle moléculaire. Dans la formule, on a CH4. On a donc un seul atome de carbone (aucun chiffre indiqué) et quatre atomes d’hydrogène. On va alors la représenter comme ceci :
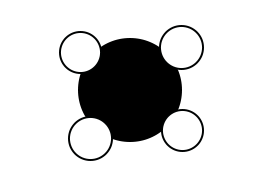
Un atome de carbone au centre et quatre molécules d’hydrogène de part et d’autre de l’atome de carbone, de façon symétrique.
Précision : les atomes d’hydrogène sont, dans les représentations, plus petits que les atomes de carbone, d’hydrogène et d’azote qui sont, eux, à peu près de la même taille.
Masse volumique
Masse volumique
I. Masse et volume
La masse $m$ s’exprime en kg et mesure la quantité de matière qu’il y a dans un objet. Plus un objet est massique et plus il y a de matière à l’intérieur. Le volume qui se note $V$ et qui s’exprime en m3 ou en L, mesure l’espace pris par un objet.
II. Formule de la masse volumique
Pour introduire ce qu’est la masse volumique et bien comprendre ce qu’elle représente, on fait l’expérience suivante :
On prend 1 m3 d’or et 1 m3 d’aluminium, on a donc le même volume d’or que celui d’aluminium. On veut mesurer leur masse respective. On constate que la masse d’1 m3 d’or est de 19 300 kg et la masse d’1 m3 d’aluminium est de 27 00 kg.
Même si on a le même volume, on n’a pas forcément la même masse. La masse volumique exprime cela, en voici la formule : $m = \rho \times V.$
$\rho$ est une espèce de p recourbé qui représente la masse volumique. La masse s’exprime en kg dans son unité officielle, le volume V s’exprime en m3 et la masse volumique $\rho$ s’exprime en kg/m3 ou en kg/L si le volume est en L.
III. Mesure de la masse volumique
Pour mesurer la masse volumique d’un liquide, il faut avoir la masse et le volume. On prend une éprouvette graduée que l’on place sur une balance, on appuie sur « tare » et ensuite on verse un certain volume de liquide puis on relève la masse indiquée. Le volume est indiqué sur l’éprouvette graduée et la masse sur la balance. Pour déterminer la masse volumique, on a la relation :
$\rho = \dfrac{m}{V}$, puisque $m = \rho \times V.$
Exemple pour un liquide
On a une masse de 0,1 kg et un volume de 0,1 L. On a alors : $\rho = \dfrac{0,1}{0,1}= 1 \ kg/L$. C’est le cas de l’eau par exemple.
Exemple pour un solide
Si le solide a une forme géométrique simple, dont on peut calculer facilement le volume, comme un cylindre par exemple, alors il suffit de mesurer la hauteur et le rayon du cylindre.On calcule à partir de cela le volume et on le pose sur une balance pour avoir la masse. Pour déterminer la masse volumique, on fait le même calcul que précédemment.
Si maintenant on a un solide de forme indéfinie : pour la masse, on va toujours utiliser une balance. Pour le volume, on peut utiliser la méthode suivante : on met une certaine quantité de liquide, un volume $V_1,$ on immerge entièrement l’objet ici et on mesure le volume $V_2.$ Pour avoir le volume de l’objet, il suffit de faire $V = V_2-V_1.$ Cette technique est possible uniquement si l’objet coule et ne flotte pas dans l’eau.


