Expression de l'aire d'un triangle
Expression de l’aire d’un triangle : $A = \dfrac{1}{2} ab \sin(\widehat{C})$
I) Expression de l’aire d’un triangle à l’aide du sinus d’un angle du triangle
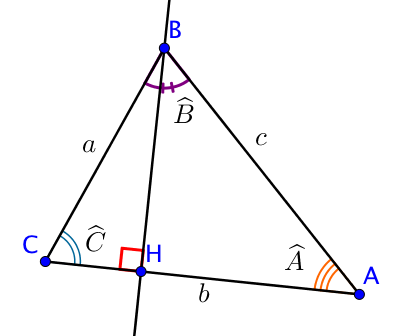
Soit $ABC$ un triangle quelconque,
on note $a$ la longueur $[BC]$, située en face du point $A$,
on note $b$ la longueur $[AC]$, située en face du point $B$,
on note $c$ la longueur $[AB]$, située en face du point $C$,
on trace la hauteur issue de $B$ (ou relative à $[CA]$) et on note $H$ le point d’intersection de la hauteur et du segment $[AC]$.
L’aire du triangle $ABC$ est donnée par la formule : $A = \dfrac{1}{2} ab \sin(\widehat{C})$
Preuve :
La formule usuelle pour calculer l’aire d’un triangle est : $\dfrac{\text{base} \times \text{hauteur}}{2} = \dfrac{b \times BH}{2}$.
On cherche à exprimer la valeur de la hauteur $[BH]$ à partir des données précédentes.
On se place alors dans le triangle rectangle $BCH$, rectangle en $H$ et on utilise l’angle $\widehat{C}$.
On souhaite alors relier $a, \, BH$ et $\widehat{C}$ : on utilise donc la formule du sinus :
$\sin(\widehat{C}) = \dfrac{\text{côté opposé}}{\text{hypoténuse}} = \dfrac{BH}{a}$.
Ainsi, $BH = a \times \sin(\widehat{C})$.
En remplaçant dans la formule de l’aire la valeur de $BH$ par celle trouvée précédemment, on obtient la formule suivante :
$\text{Aire } = \dfrac{1}{2} ab \sin(\widehat{C})$
II) Application
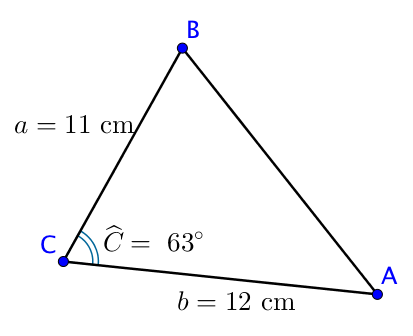
Soit $ABC$ un triangle dont certaines dimensions sont données sur le schéma suivant.
1) Calcul de l’aire du triangle $ABC$
On applique pour se faire la formule précédente.
$\text{Aire } = \dfrac{1}{2} ab \sin(\widehat{C}) = \dfrac{11 \times 12 \times \sin(63°)}{2} \approx 58,8 $ cm$^2$.
2) Calcul de la hauteur
Pour calculer la hauteur, on utilise la formule usuelle de l’aire qui fait intervenir la hauteur :
$\mathcal{A} = \dfrac{\text{base} \times \text{hauteur}}{2}$
On isole alors la hauteur de cette équation car les autres valeurs qui interviennent sont connues :
$h = \dfrac{2 \mathcal{A}}{\text{base}}$
Ainsi, $h \approx \dfrac{2 \times 58,8}{12} \approx 9,8$ cm.