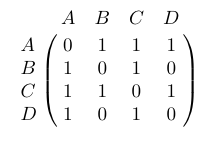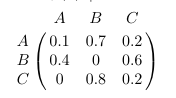Vocabulaire des graphes
Vocabulaire des graphes
Définition
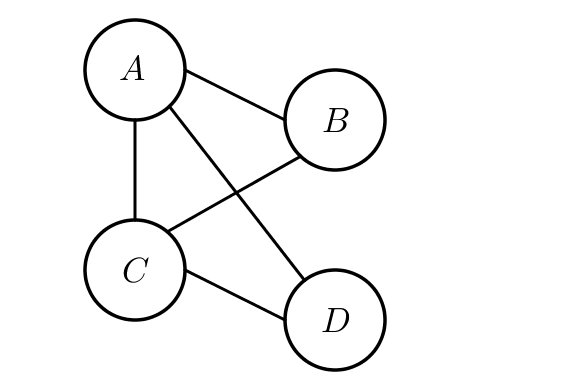
Un graphe est un ensemble de points reliés entre eux.
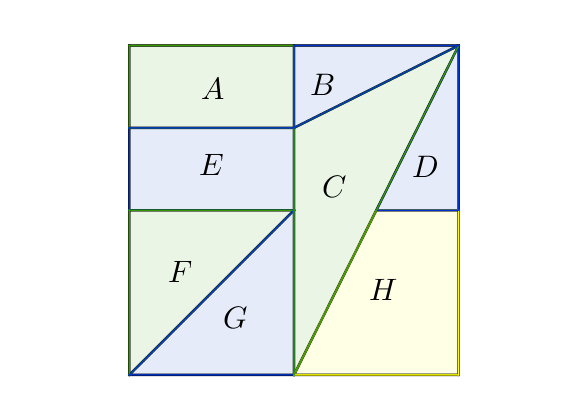
Dans la suite, on considéra comme exemple le graphe suivant.
Les points sont appelés des sommets. Le nombre total de sommets est appelé l’ordre : ici l’ordre vaut 4.
Deux sommets sont adjacents si ils sont reliés entre eux. Par exemple, $B$ et $D$ ne sont pas adjacents.
Les segments reliant deux sommets sont des arêtes.
Le degré d’un sommet correspond au nombre d’arêtes partant de ce commet. Par exemple, trois arêtes partent du sommet $A$ : $A$ est de degré 3.
Une chaîne de sommets est une liste de sommets reliés par des arêtes. Un cycle est une chaîne débutant par un sommet et terminant par ce même sommet. Par exemple $ABCD$ est une chaîne et $ABCA$ est un cycle.
La longueur d’une chaîne est le nombre d’arêtes composant cette chaine. Il ne faut donc pas compter le nombre de sommets ! Ainsi, la longueur de la chaine $ABCD$ est 3.
Un graphe est complet si tous les sommets sont reliés entre eux par une arête. Ici, $B$ et $D$ ne sont pas reliés entre eux, le graphe n’est donc pas complet.
Un graphe est connexe si tous les sommets sont reliés par une chaine quelconque. Ici le graphe est connexe.
Une chaine eulérienne est une chaine qui passe par chaque arête une seule fois : c’est le cas de la chaine $CDACBA$.
Un cycle eulérien est une chaîne fermée passant par chaque arête d’un graphe. Ici, il n’existe pas de cycle eulérien.
La matrice du graphe contient des 0 et des 1. Si il y a un 1 à l’intersection de la ligne $i$ et de la colonne $j$, alors il existe une arête reliant le sommet $i$ au sommet $j$. Sinon, aucune arête relit ces deux sommets et on l’indique alors par un 0.
Propriétés :
La somme des degrés des sommets vaut le double du nombre d’arêtes.
Si sur l’ensemble des sommets, seulement deux sont de degré impair, alors il existe une chaîne eulérienne. Cette propriété montre l’existence d’une telle chaîne mais ne la donne pas.
Si tous les degrés sont pairs, alors il existe un cycle eulérien.
Colorier un graphe
Colorier un graphe
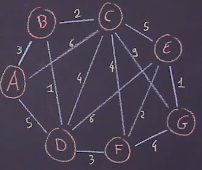
On souhaite colorier un graphe avec un minimum de couleurs en ayant comme contrainte que deux sommets voisins aient des couleurs différentes. Le nombre minimal de couleurs est appelé le nombre chromatique.
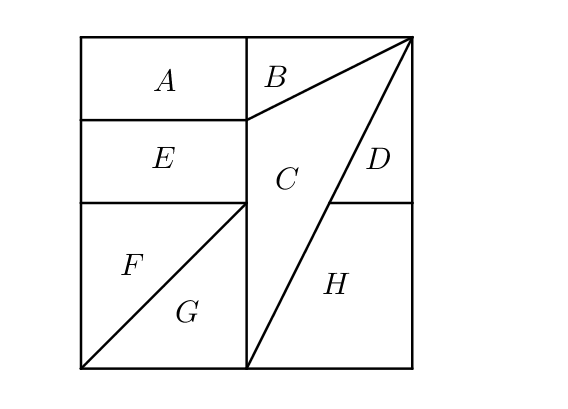
On dispose du drapeau suivant que l’on souhaite colorier.
Pour se faire, on réécrit ce drapeau sous forme d’un graphe dont les sommets représentent les différentes zones et les arêtes traduisent que deux zones se touchent.
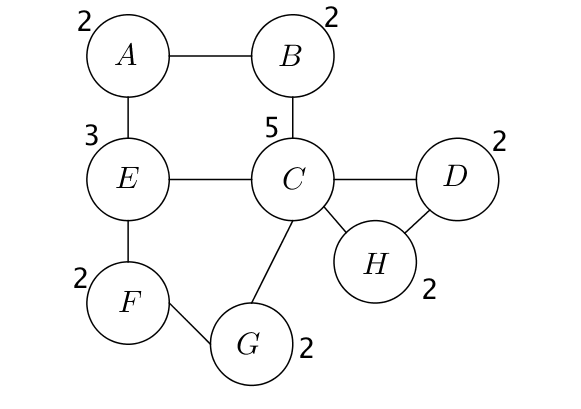
On écrit sur chaque sommet son degré.
Pour colorier le graphe, on utilise l‘algorithme de Welsh-Powell.
On classe par ordre décroissant du degré les différents sommets sur la première ligne du tableau et par ordre alphabétique.
On associe au sommet de plus haut degré la première couleur $c_1$ puis on donne à tous les sommets qui ne sont pas adjacents à ce sommet la couleur $c_1$.
Ici, le sommet de plus haut degré est le sommet $C$. Les sommets qui ne sont pas voisins avec lui sont $A$ et $F$.
On complète ensuite une nouvelle ligne du tableau en attribuant au premier sommet qui n’a pas encore été coloré une nouvelle couleur $c_2$, ainsi qu’aux autres sommets qui ne lui sont pas voisins.
C’est donc le sommet $E$ qui reçoit la couleur $c_2$ puis $B, D$ et $G$.
Enfin, on continue de même l’algorithme. Ici, on attribue au dernier sommet $H$ une nouvelle couleur $c_3$.
| $C$ | $E$ | $A$ | $B$ | $D$ | $F$ | $G$ | $H$ | Sommet |
| 5 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | Degré |
| $c_1$ | x | $c_1$ | x | x | $c_1$ | x | x | Couleur 1 |
| $c_2$ | x | $c_2$ | $c_2$ | x | $c_2$ | x | Couleur 2 | |
| $c_3$ | Couleur 3 |
Le nombre chromatique est donc 3.
Vocabulaire des graphes orientés
Vocabulaire des graphes orientés
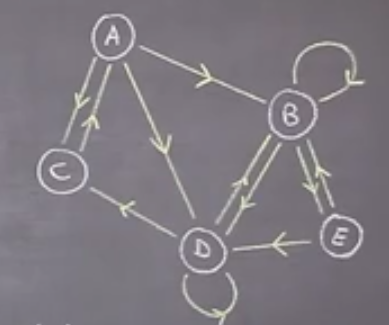
On considère dans la suite le graphe orienté suivant :
Vocabulaire
Un graphe orienté est un graphe dans lequel chaque arête a un sens.
Une arête s’appelle alors un arc.
Une boucle est un arc pour lequel l’événement de départ et l’événement d’arrivée sont identiques : on part de l’événement et on revient sur lui même.
Un chemin est une chaîne formée d’arcs, en respectant le sens des flèches, comme par exemple $ABED$. Un chemin peut être fermé, comme par exemple $ADCA$.
Un circuit est un chemin fermé pour lequel chaque arc est utilisé exactement une fois : on ne passe pas deux fois au même endroit et tous les arcs sont différents.
Matrice associée
On peut également représenter le graphe sous forme d’une matrice.
On voyage des lignes vers les colonnes et on indique par un 1 si il existe un arc liant les deux sommets et par un 0 sinon.
La diagonale peut contenir des 1 car il peut y avoir des boucles dans le graphe.
Il est possible de complexifier le graphe en ajoutant des étiquettes qui peuvent être des mots, des couleurs, des lettres…
Enfin, il est possible de rajouter sur chaque arc un poids : il s’agit d’un nombre positif ou nul que l’on indique aussi dans la matrice.
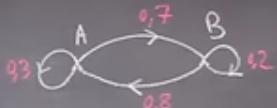
Les graphes probabilistes
Les graphes probabilistes
Les graphes probabilistes permettent de transformer une étude probabiliste en un graphe et sa matrice.
Il existe des graphes d’ordre 2 ou d’ordre 3.
Les poids sur chaque arc correspondent à la probabilité de passer d’un événement à un autre en suivant le sens de parcours imposé par la flèche.
La somme des probabilités inscrites sur les arcs partant d’un événement doit être égale à 1.
Exemples :
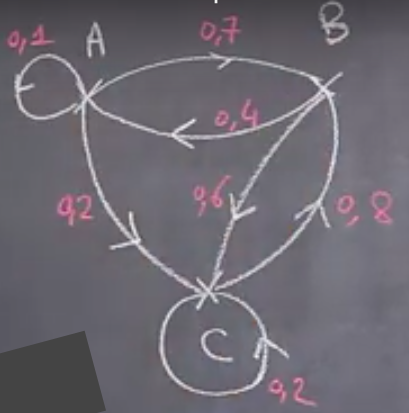
On considère le graphe d’ordre 3 suivant, et on le représente également par une matrice, contenant à l’intersection de la ligne $i$ avec la colonne $j$ la probabilité pour passer de l’événement $i$ à l’événement $j$.
En additionnant les probabilité d’une ligne, on vérifie que le résultat vaut 1.
On peut aussi considérer un graphe d’ordre 2.
$M = \left ( \begin{array}{cc} 0.3 & 0.7 \\ 0.8 & 0.2 \end{array} \right )$
Application :
On suppose que la situation que l’on étudie se traduit par le graphe d’ordre 2 précédent, que l’on peut traduire sous forme matricielle.
On considère un état $P_0 = (a \ \; b)$ initial. Pour connaitre l’état $P_1$, on multiplie $P_0$ par $M$ et ainsi de suite.
On trouve alors que pour tout $n \in \mathbb{N}, \ P_{n + 1} = P_n \times M$.
L’état $n + 1$ correspond à l’état $n$ multiplié par la matrice $M$.
Il s’agit d’une suite géométrique de raison $M$ et de terme initial $P_0$.
Ainsi, pour tout $n \in \mathbb{N}, P_n = P_0 \times M^n$. On veillera à ce que l’énoncé donne un premier terme pour $n = 0$.
On essaie de savoir si en regardant pour des états $n$ lointains, le comportement de $P_n$ atteint un état stable, c’est à dire qu’il ne bouge plus, ou encore si la suite $(P_n)$ converge.
Or si aucun des 4 coefficients n’est égal à 0, il existe un état stable, que l’on appelle $P = (x \ \ y)$.
Pour connaitre les valeurs de $x$ et $y$, on sait que la somme des probabilités vaut $1$ et comme il s’agit d’un état stable, il ne change pas lorsque on le multiplie pat la matrice $M$.
On obtient alors le système suivant : $\left \{ \begin{array}{c} PM = P \\ x + y = 1 \end{array} \right.$
Les graphes probabilistes - Exercice
Algorithme de Dijkstra
Algorithme de Dijkstra
Définition
L’algorithme de Dijkstra est un algorithme qui permet de calculer le plus court chemin entre deux sommets.
Exemple
On considère le graphe suivant, et on souhaite trouver le chemin le plus court entre $A$ et $G$.
On dessine un tableau pour représenter les différentes étapes de l’algorithme et on écrit sur la première ligne le nom des sommets par ordre alphabétiques.
La dernière colonne représente le choix à l’issue de chaque étape de l’algorithme.
On part de $A$ : on dispose de trois possibilités : soit on va en $B$, soit en $D$ soit en $C$.
En dessous de chacun des ces sommets, on inscrit sur la premier ligne les poids de chaque arrête puis on choisit le sommet qui présente l’arrête de poids moindre.
Si aucune arrête relit deux sommets, on indique une distance infinie dans le tableau.
On choisit donc le sommet $B$, et on peut ensuite rejoindre le sommet $C$ ou le sommet $D$ : on ne peut pas revenir en $A$.
Lors de l’étape précédente, on avait choisit un chemin de longueur 3, donc à chacune des distances inscrites sur les arêtes, on ajoute la distance déjà parcourue pour atteindre le point $B$.
On suppose donc que l’on part de $D$. On remplit à nouveau la ligne de $D$.
On remarque que à l’étape précédente, on aurait pu passer par $C$.
On regarde donc les possibilités offertes par $C$ que l’on compare à celles offertes par $D$ : finalement, la distance la plus courte est celle allant en $F$ depuis $D$.
On choisit donc $F$ et on regarde les possibilités de chemin depuis ce sommet. On complète la fin du tableau en suivant le même principe.
Afin d’obtenir le chemin le plus court, il ne s’agit pas d’écrire tous les sommets inscrits dans la colonne “choix”, mais de remonter le raisonnement.
Ici, le chemin le plus court est $A-B-D-F-E-G$.
| $A$ | $B$ | $C$ | $D$ | $E$ | $F$ | $G$ | Choix |
| X | $3A$ | $6A$ | $5A$ | $\infty$ | $\infty$ | $\infty$ | $B$ |
| $5B$ | $4B$ | $\infty$ | $\infty$ | $\infty$ | $D$ | ||
| $8D$ | $10D$ | $7D$ | $\infty$ | on choisit $C$ depuis $B$ | |||
| $5B$ | $C$ | ||||||
| $10C$ | $9C$ | $14C$ | on choisit $F$ depuis $D$ | ||||
| $7D$ | $F$ | ||||||
| $9F$ | $11F$ | $E$ | |||||
| $10E$ | $G$ |