Le principe d'inertie
Le principe d’inertie
I. Qu’est-ce qu’un principe ?
Définition : Un principe est une loi qu’aucune expérience n’a invalidée.
Cette loi est considérée comme valable tant qu’aucune expérience n’a montré qu’elle est fausse. Un principe ne se démontre pas.
II. Principe d’inertie
Dans un référentiel Galiléen, si un système est en mouvement rectiligne uniforme ou est immobile, alors les forces qui s’appliquent sur lui se compensent ou aucune force ne s’applique.
La réciproque est elle aussi vraie : si les forces qui s’appliquent sur un système se compensent ou qu’aucune force ne s’applique, alors il est en mouvement rectiligne uniforme ou est immobile.
Mouvement rectiligne : mouvement dont le trajectoire est une droite.
Mouvement uniforme : mouvement à vitesse constante.
III. Application : saut en parachute
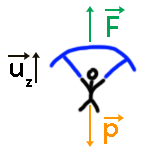
$u_z$ est le vecteur unitaire qui indique l’axe vertical. On considère le système {Homme + parachute}.
Deux forces s’appliquent sur le système :
$\overrightarrow{F}$, la force de l’aire sur la voile dirigée vers le haut.
$\overrightarrow{P}$, le poids de l’ensemble {homme + parachute} dirigé vers le bas.
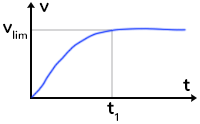
Sur ce graphique on trouve $t$ le temps en abscisse et $v$ la vitesse verticale en ordonnée.
Au départ (t=0) la vitesse est nulle car l’homme ne tombe pas. Puis sa vitesse augmente jusqu’à atteindre une vitesse limite $v_{lim}$ à la date $t_1$.
À partir de cette date ($t>t_1$) la vitesse est constante et égale à $v_{lim}$. On est donc en mouvement rectiligne uniforme car le parachutiste et sa voile tombent verticalement (ligne droite) et à vitesse constante.
En appliquant le principe d’inertie on déduit que les forces qui s’appliquent au système se compensent. Cela s’écrit mathématiquement : $\overrightarrow{P} + \overrightarrow{F} = \overrightarrow{0}$.
On peut donc calculer la valeur de la force de l’air : $\overrightarrow{F} = – \overrightarrow{P} = m_{tot} \times g \times \overrightarrow{u_z}$ (on rappelle $\overrightarrow{P} = – m_{tot} \times g \times u_z$).
Durant la phase d’accélération ($t<t_1$), la vitesse n’est pas constante. D’après le principe d’inertie, les forces ne se compensent pas :
$\overrightarrow{P} + \overrightarrow{F} \neq \overrightarrow{0}$.
Cela s’explique par la fait qu’au début du saut, la force de frottement de l’air est faible. Elle augmente progressivement jusqu’à atteindre à $t_1$ la valeur que l’on a calculé précédemment lorsqu’elle compense le poids.
Variation de la vitesse et forces : la contraposée du principe d'inertie
Variation de la vitesse et forces : la contraposée du principe d’inertie
I. Principe d’inertie
Pour rappel, dans une situation où un mobile est en mouvement rectiligne uniforme (MRU) ou immobile, cela implique que les forces se compensent (la somme vectorielle des forces vaut le vecteur nul), ou qu’aucune force ne s’applique sur le système. L’inverse est vraie aussi : si aucune force ne s’applique ou si les forces se compensent, alors le système est en mouvement rectiligne uniforme ou alors immobile.
II. Conséquence du MRU
Voici un schéma d’un mouvement rectiligne uniforme :
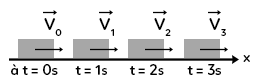
Un système rectangulaire est en MRU vers la droite. Cela veut dire que c’est une trajectoire rectiligne à vitesse constante.
On a quatre instants : $t=0\ s, 1\ s, 2 \ s, 3 \ s.$ A chaque fois, il y a une seconde entre chaque étape donc cela veut dire que la distance entre chaque boîte est la même. La vitesse à chaque instant est la même car nous sommes dans le cas d’un MRU. Le vecteur vitesse a la même direction, car c’est un mouvement rectiligne.
Si le vecteur $\overrightarrow{v_1}$ était un peu vers le haut, le mobile serait en train de monter et ce ne serait pas un mouvement rectiligne.
On a alors : $\overrightarrow{v_0} = \overrightarrow{v_1} = \overrightarrow{v_2} = \overrightarrow{v_3}$.
Le vecteur variation de vitesse $\Delta\overrightarrow{v}$ vaut $\overrightarrow{v_{après}}-\overrightarrow{v_{avant}}$.
Si on prend $\Delta \overrightarrow{v} (t=0)=\overrightarrow{v_1} – \overrightarrow{v_0} = \overrightarrow{0}$.
On a également à t = 1 s, $\Delta\overrightarrow{v} (t=0)=\overrightarrow{v_2} – \overrightarrow{v_1} = \overrightarrow{0}$.
De manière générale, peu importe le temps où l’on calcule $\Delta \overrightarrow{v}$, $\overrightarrow{v} = \overrightarrow{0}$.
On peut donc en conclure qu’un MRU implique $\Delta \overrightarrow{v} = \overrightarrow{0}$.
S’il est immobile, c’est encore plus simple puisque sa vitesse est toujours nulle donc $\Delta \overrightarrow{v} = \overrightarrow{0}$. Réciproquement, si $\Delta \overrightarrow{v} = \overrightarrow{0}$, on se trouve dans un MRU.
III. Contraposée du principe d’inertie
Si $ \Delta \overrightarrow{v} \ne \overrightarrow{0},$ alors les forces qui s’appliquent sur le système ne se compensent plus. C’est la contraposée du principe d’inertie.
Réciproquement, si les forces qui s’appliquent sur un système ne se compensent pas alors $\Delta \overrightarrow{v} \ne \overrightarrow{0}$.
Exemple : la chute libre
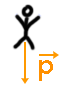
On prend un homme qui saute d’un avion, et, la seule force qui l’attire est le poids. On a négligé les forces de l’air. Le poids est une force d’attraction vers le bas. Puisqu’il n’y a qu’une force, il n’y a pas moyen de compenser. On se trouve bien dans la contraposée du principe d’inertie.
Comme il n’y a qu’une force, qui ne se compense pas avec elle-même alors $\Delta\overrightarrow{v} \ne \overrightarrow{0}$. Cela veut dire que le vecteur vitesse évolue avec le temps puisque la différence des vecteurs vitesse est différente de $0.$
En effet, si on regarde ce qui se passe dans la chute, à $t = 0 \ s$ c’est le moment où l’homme quitte l’avion. Sa vitesse est encore nulle. Il n’a pas encore commencé à tomber. Une seconde plus tard, il a pris de la vitesse : on l’appelle $\overrightarrow{v_1}$. Deux secondes plus tard, il a pris encore de la vitesse : c’est $\overrightarrow{v_2}$.Quand il tombe, il accélère. La flèche est plus grande.
On va s’intéresser aux $\Delta\overrightarrow{v}.$
Au début, $\Delta\overrightarrow{v} = \overrightarrow{v_1}-\overrightarrow{v_0} \ne \overrightarrow{0}$.
Les deux vecteurs ne se compensent pas car il ne reste que $\overrightarrow{v_1}.$
Donc c’est bien différent du vecteur nul. A l’étape suivante, la différence des deux vecteurs m’en donne un autre. Donc, on n’a pas non plus un vecteur nul. En conclusion, ce que l’on avait prévu avec la contraposée du principe d’inertie est tout à fait exact.