Solides et volumes
Patrons de solides
Patrons de solides
Définition
Un patron est une figure plane, que l’on peut découper, et qui une fois pliée reconstitue un solide de l’espace.
Tous les solides n’ont pas de patron. En effet, la sphère ne possède pas de patron.
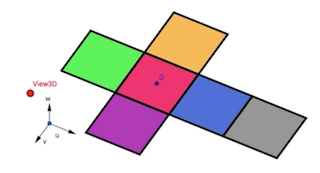
Patron d’un cube
On remarque les 6 faces identiques du cube. Il existe 11 patrons possibles.
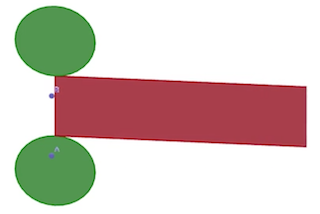
Patron d’un cylindre
Les bases sont des disques et la face latérale est un rectangle. La largeur du rectangle est la hauteur du cylindre, et la longueur du rectangle est le périmètre de chacune des deux bases.
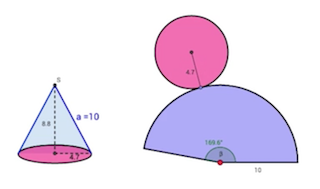
Patron d’un cône
L’apothème du cône qui est la longueur en bleue sur le schéma correspond au rayon de la portion de disque qui donne une fois plié la surface latérale. La base du cône est un disque.
La longueur de l’arc de cercle issu la portion de disque est égale au périmètre de la base.
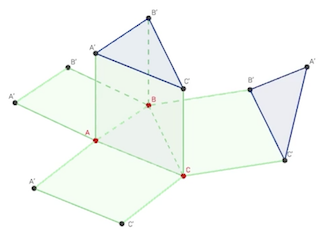
Patron d’un prisme droit
On considère ici un prisme à base triangulaire. Son patron est composé de deux triangles superposables et de trois rectangles.
Patron d’un pyramide
On considère dans la suite une pyramide à base carrée. La base est un carré et les faces latérales sont des triangles isocèles égaux.