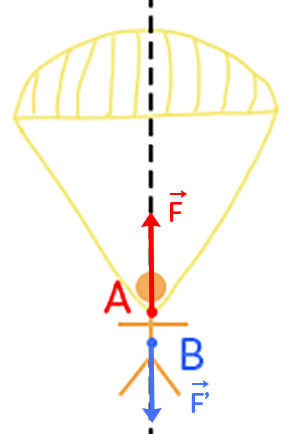
Représentation des forces
Voyons comment représenter des forces à travers l’exemple d’un homme qui effectue un saut en parachute.
Une force modélise une action mécanique. Pour représenter des forces, il faut voir les actions que subit l’objet d’étude. Ici, l’objet d’étude est l’homme qui effectue son saut en parachute. Cet homme est en interaction de contact avec le parachute puisqu’il est en contact direct avec le parachute. Il est en interaction à distance avec la Terre puisqu’il est attiré par le centre de la Terre. L’homme qui est l’objet d’étude subit une interaction avec le parachute et une interaction de la part de la Terre.
On modélise ces deux actions par deux forces, qui sont en fait des flèches. Pour représenter ces flèches, il faut préciser le point d’application, la direction, le sens et la valeur ou intensité.
Pour la représentation de la première force, qui est la force exercée par le parachute sur l’homme, on va d’abord voir le point d’application. C’est le point de contact entre l’homme et le parachute, qui est le point A. De manière générale, quand on a une interaction ou action de contact, le point d’application de la force qui la représente se trouve toujours au niveau du contact. La direction est verticale, puisque le parachute soutient l’homme. C’est la droite représentée en pointillés noirs. Le sens c’est celui du parachute puisque le parachute tire l’homme vers le haut. Pour la valeur, on suppose qu’elle est de 500 N. Pour représenter la force, on utilise une échelle : par exemple 1 cm vaut 100 N. Sur la feuille, comme on a 500 N cela fera 5 cm. Pour représenter cette force, on part du point A, ont suit la direction et on va vers le haut pour faire une flèche de 5 cm. On aura la force exercée par le parachute sur l’homme.
Voyons la deuxième force, celle exercée par la Terre sur l’homme. Par définition, le point d’application va s’appliquer au centre puisque c’est une interaction à distance. La direction est verticale puisque la Terre attire verticalement les corps. Cette fois-ci, le sens n’est pas vers le haut mais vers le bas. Par exemple, la valeur de cette force est ici de 700 N. Puisqu’on a l’échelle 1 cm qui vaut 100 N et pour représenter cette force, on va partir du point B, on va suivre la direction verticale en prenant le sens vers le bas et on va faire une flèche de 7 cm.
Dans cet exemple, on constate que la force exercée par la Terre est supérieure à celle exercée par le parachute donc celui-ci va descendre.
Représentation de forces : cas du poids
Représentation de forces : cas du poids
Comment représenter le poids d’un objet ?
Le poids est la force qui modélise l’attraction gravitationnelle exercée par la Terre sur les objets qui sont à sa surface. Pour représenter cette force, que l’on appelle le poids, il faut préciser, comme à chaque fois :
– le point d’application,
– la direction,
– le sens,
– la valeur ou intensité.
Exemple
Une pomme de masse m = 0,15 kg. C’est un cas très général que l’on peut appliquer à tous les objets dont il faut représenter le poids.
Le point d’application sera toujours le centre de l’objet puisqu’il s’agit d’une interaction à distance. On l’appelle couramment le centre de gravité et on le note souvent G. Ici, on va l’appliquer au niveau du centre de la pomme.
La direction sera toujours verticale pour le poids et le sens vers le bas.
Pour la valeur ou intensité du poids, on utilise la formule : $P = m \times g.$
$m$ étant la masse de l’objet, ici la masse de la pomme donc : 0,15 kg, et $g$ étant l’intensité de la pesanteur que l’on donnera (9,8 N/kg sur Terre).
On obtient : $P = 0,15 \times 9,8 = 1,47 \ N.$
Pour représenter le poids, il faut choisir une échelle ou alors elle sera imposée. Ici, on a choisi l’échelle 1 N vaut 10 cm. Donc 1,47 N vaut 14,7 cm. Il suffit de faire un produit en croix :
$\dfrac{1,47 \times 10}{1} = 14,7 \ cm.$
Pour représenter le poids de la pomme, on part ensuite du point d’application G, on va à la verticale, vers le bas et on fait un segment fléché de 14,7 cm. On peut aussi noter P avec une petite flèche dessus.
Mouvements et vitesse
Comment décrire des mouvements et représenter la vitesse sur une trajectoire ? Pour décrire un mouvement, il faut préciser sa trajectoire et l’évolution de la valeur de la vitesse.
I. Trajectoire
La trajectoire est l’ensemble des positions qui sont prises par un objet. Il y a deux types de trajectoires spécifiques :
– Lorsque l’on peut relier les positions prises par l’objet par une droite. Elle peut être horizontale, verticale ou oblique. A ce moment-là, on va dire que la trajectoire est rectiligne.
– Lorsque l’on peut relier les positions de l’objet par un cercle, à ce moment-là, on dit que la trajectoire de l’objet est circulaire.
– Si on n’a ni une droite, ni un cercle, on peut dire que la trajectoire est variée.
II. Évolution de la valeur de la vitesse
Si la vitesse ne varie pas, c’est-à-dire, qu’elle reste la même tout au long du mouvement, on dit que le mouvement est uniforme. Si la vitesse augmente, on dit que le mouvement est accéléré. S’il diminue, on dit qu’il est ralenti. Dans certains cas, on ne voit pas la distinction uniforme-accéléré-ralenti mais uniquement uniforme et non uniforme. Les deux derniers cas sont donc les cas où la vitesse est non uniforme et donc non constante. Elle change de valeur au court du temps.
III. Représentation de la vitesse en un point
On a un mouvement qui a une trajectoire de courbe. Le mouvement étant de A vers B. On représente la vitesse au point A. On représente cette vitesse par une flèche. Il faut donc préciser le point d’application, la direction, le sens et la valeur.
Le point d’application est le point A puisqu’on veut représenter la vitesse au point A. La direction est tangente à la trajectoire au point A. En pratique, on prend une règle, on part du point A et on longe la trajectoire. Ensuite on poursuit la droite pour avoir la direction. Le sens est le sens de la trajectoire, c’est-à-dire, de A vers B. Il est représenté par une flèche. La longueur de la flèche doit être proportionnelle à la valeur de la vitesse. Cela veut dire que plus la vitesse sera importante, plus la flèche représentée aura une longueur importante.