Codage des entiers
Codage des entiers
En binaire, un nombre correspond à une suite de 0 et de 1, que l’on convertit en une écriture en puissance de 10 usuelle en sommant le produit des chiffres du nombre par des puissances de 2 successives.
On considère $n = overline{x_nx_{n-1}…x_1x_0}^2$ avec $x_n in {0; 1 }$.
Alors, $n = displaystyle sum_limits{k = 0}^n x_k 2^k = x_0 times 2^0 + x_1 times 2^1 + … +x_n times 2^n$.
Pour coder un tel entier, on utilise une mémoire composée de $n + 1$ bits, avec $n + 1 geq 8$.
Le bit de rang 0 est appelé bit de poids faible.
Le bit de rang $n$ est appelé bit de poids fort.
Il y a $n + 1$ bits.
| n | n-1 | n-2 | 2 | 1 | 0 |
I. Codage des entiers naturels
On souhaite par exemple coder $19$. On sait que $19 = overline{10011}^2$.
On écrit donc ces chiffres en partant de la droite et du bit de poids faible. On remplit le reste des cases par des 0.
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| n | n-1 | n-2 | … | 4 | 3 | 2 | 1 | 0 |
On suppose que $n + 1 = 8$.
Dans une telle situation, le nombre maximal que l’on peut coder correspond au nombre où tous les chiffres sont des 1 :
$displaystyle sum_limits{k = 0}^7 2^k = 2^{7 + 1} – 1 = 2^8 – 1 = 255$.
En utilisant 8 bits on peut coder tous les entiers compris entre 0 et 255.
De même, si on suppose que $n + 1 = 16$, on peut écrire tous les entiers compris entre 0 et $2^{16} – 1 = 65535$.
II. Codage des entiers relatifs
1. Méthode du nombre binaire signé
Une des solutions est l’utilisation de nombre binaire signé.
Dans ce cas, le $n + 1$ème bit (qui correspond au bit de rang $n$) est réservé pour coder le signe du nombre considéré.
L’usage du $1$ dans le bit de poids fort indique que le nombre est négatif.
Exemple :
On veut coder l’entier $-10 = – overline{1010}^2$.
On écrit alors dans les bits la série suivante, en inscrivant dans le bit de poids fort le chiffre $1$ car le nombre codé est négatif.
| 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| n | n-1 | n-2 | … | 4 | 3 | 2 | 1 | 0 |
L’usage de réserver le bit de poids fort au signe implique la perte d’un bit et donc une réduction des possibilités de codage des nombres positifs.
En effet, si $n + 1 = 8$, il n’y a que 7 bits pour coder les nombres.
Le plus grand nombre vaut alors $displaystyle sum_limits{k = 0}^6 2^k = 2^{6 + 1} – 1 = 2^7 – 1 = 127$.
On peut alors coder tous les entiers relatifs compris entre $-127$ et $+127$.
Si $n+ 1 = 16$, il est alors possible de coder tous les entiers relatifs compris entre $-32767$ et $32767$.
En informatique, $0$ est considéré comme un nombre positif et est donc codé en n’utilisant que des $0$.
Il reste donc une possibilité qui correspond au $0$ négatif et codé en utilisant un $1$ dans le bit de poids fort et des $0$ ailleurs, qui est utilisé pour coder l’entier $-2^n$.
On code alors tous les entiers relatifs compris entre $-2^n$ et $-2^{n-1}$.
2. Méthode des compléments à 2
Principe
Une autre solution est l’utilisation de la méthode des compléments à 2.
Si l’entier est positif, la méthode ne change pas.
Si l’entier est négatif, on commence par coder sa valeur absolue, c’est à dire son opposé qui est positif.
On code alors selon la méthode binaire signé positif puis on complémente tous les bits non utilisé à 1 puis on ajoute 1.
Exemple
On souhaite coder l’entier relatif $-14$.
On sait que $|-14| = 14$.
On commence donc par coder sa valeur absolue donc $14$, le bit de poids fort contient un 0 car 14 est positif.
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
Dans une nouvelle ligne, on remplace les 0 par des 1 et réciproquement.
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
A ce nouveau nombre on ajoute $1$ dans le bit de poids faible, en se souvenant que $1 + 1$ correspond à une retenue de 1 pour la colonne suivante.
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 |
Remarque
Dans la méthode précédente, on voit qu’en ajoutant 1, il est possible de propager la retenue dans chaque colonne si tous les bits contenaient des 1.
Se faisant, on obtiendrait alors un chiffre qui devrait être stocké plus loin que le bit de poids fort.
Or, si tous les bits contenaient des 1, cela signifie que l’on codait le nombre de contenant que des 0, c’est à dire l’entier 0 qui n’est pas négatif : il ne sera donc jamais codé en utilisant la méthode des compléments à 2.
Si les entiers codés sont différents de 0, alors le codage de la valeur absolue fait au moins apparaitre un 1, donc le complément fait apparaitre au moins un 0 : la propagation de la retenue éventuelle est donc forcément stoppée.
Exemple
Codage de $-1$ en reprenant ces trois étapes.
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
On se propose de regarder d’un point de vue mathématique les opérations que l’on réalise pour le codage.
La première étape correspond au codage de la valeur absolue $|x|$ du nombre $x$, qui ne contient que des 0 sauf le bit de poids faible qui contient un 1.
Pour trouver le complément à 1 de ce nombre, on soustrait en réalité le nombre ne contenant que des 1 et la valeur absolue du nombre codé.
Le nombre ne contenant que des 1 correspond à $2^8 – 1$.
On vient donc de coder l’entier naturel $2^8 – 1 – |x|$.
Si on ajoute $1$ à ce nombre, on trouve alors $2^8 – |x|$, dans le codage des entiers naturels.
Finalement, il ne s’agit donc pas du complément à 2 mais à $2^8$ que l’on code, mais pour simplifier, on dira complément à 2.
Technique pour écrire rapidement le complément à 2
Pour écrire plus rapidement le complément à 2, il existe des techniques.
Une technique consiste à coder la valeur absolue du nombre, puis de partir du bit de poids faible et de recopier les chiffres jusqu’au premier 1 inclus.
Les chiffres suivants sont inversés par rapport au codage de la valeur absolue.
Exemple avec le codage de -20 :
On code 20 :
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
Puis on obtient:
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
Intérêt d’une telle méthode
On code par exemple par la méthode du binaire signé les entiers 3 et $-4$.
Si on somme les deux séries de 8 bits obtenus deux à deux, on obtient alors un nouveau nombre qui n’est pas égal à $-1$
En utilisant la méthode des compléments à 2, on obtient en addition bit à bit le nombre -1.
Nombres flottants 2
Nombres flottants 2
On pourra se référer au cours Nombres flottants 1 pour revoir les notions d’écriture de nombres réels en base 2 avec une partie décimale, de mantisse et d’exposant normalisés ou non.
Pour coder un nombre flottant, on fait ici l’hypothèse de travail d’un code sur 8 bits.
Le premier bit, le bit de poids fort, est réservé au bit de signe. On attribue 4 bits pour la mantisse. On se rappellera qu’en écriture normalisée, la mantisse ne contient qu’un 1 à gauche de la virgule ce qui permet de l’omettre dans le codage et donc de gagner un bit avec cette convention. On écrit en résumé les décimales du nombre en écriture normalisée.
Le nombre minimal que l’on peut écrire en ne considérant que la mantisse correspond à des 0 sur les 4 bits de la mantisse. Or, l’écriture étant normalisée, cela revient à écrire le nombre $overline{1,0000}^2$ c’est à dire 1.
Le nombre le plus grand correspond au nombre avec des 1 pour chacun des bits, soit $overline{1,1111}^2 = 1 + dfrac{1}{2} + dfrac{1}{4} + dfrac{1}{8} + dfrac{1}{16} = 1,9375$.
L’exposant est codé sur les bits restants : $8 – 1 – 4 = 3$. Or chaque bit peut prendre deux valeurs.
Ainsi 3 bits permettent de représenter $2^3 = 8$ entiers consécutifs, que l’on prendra pour l’exemple variant de $-3$ à $4$.
Le nombre flottant maximal que l’on peut coder correspond donc au produit de la mantisse maximale par l’exposant maximal : $x_{max} = overline{1,1111}^2 times 2^4 = left ( 1 + dfrac{1}{2} + dfrac{1}{4} + dfrac{1}{8} + dfrac{1}{16} right ) times 2^4 = 2^4 + 2^3 + 2^2 + 2^1 + 1 = 31$.
De même, le nombre flottant positif minimal que l’on peut coder correspond au produit de la mantisse minimal par l’exposant minimal, soit $x_{min} = overline{1,0000}^2 times 2^{-3} = 2^{-3} = 0,125$
L’écart minimal correspond à la soustraction du deuxième plus petit nombre flottant positif et du plus petit nombre flottant positif.
$epsilon = overline{1,0001}^2 times 2^{-3} – overline{1,0000}^2 times 2^{-3} = left (1 + dfrac{1}{16} right ) times 2^{-3} – 0,125 = 0,1328125 – 0,125 = 0,0078125. $
Cet écart correspond à différence minimale que doivent avoir deux nombres pour être considérés comme différents par l’ordinateur.
Dans la pratique, en notamment avec Python, le codage des nombres flottants se fait avec le code IEEE 754, en double précision. La répartition des bits se fait comme suit : 1 bit de signe, 54 bits pour la mantisse et 11 bits pour l’exposant, ce qui permet de coder des exposants variant de -1023 à 1024.
Ainsi, le plus grand nombre que l’on peut coder vaut $x_{max} = 10^{308}$ et le plus petit positif $x_{min} = 10^{-308}$. De plus, l’écart minimal vaut $epsilon = 2^{-1077} approx 10^{-325}$.
Codons par exemple le nombre flottant $x = -0,25$ sur 8 bits.
Il faut d’abord écrire le nombre en binaire. On peut alors remarquer que $x = -dfrac{1}{4} = -dfrac{1}{2^2} = -2^{-2} = -overline{0,01}^2$. En écriture normalisée, on a : $-overline{1,0000}^2 times 2^{-2}$.
Il reste à présent à coder l’exposant -2 selon la méthode du complémentation à 2. Pour cela, on commence par coder la valeur absolue de -2 c’est à dire 2. Sur 3 bits, l’écriture binaire vaut $010$. Pour coder le signe, on utilise le complémentation à 2, à savoir inverser les 0 et les 1 puis ajouter 1 sur le bit de poids faible. Cela donne alors $110$.
Finalement, le code de $x$ est le suivant 1 110 0000. Le premier 1 correspond au bit de signe, les bits 110 correspondent à l’exposant, et 0000 correspondent à la mantisse (on se rappellera que l’on n’écrit pas le 1 à gauche de la virgule en écriture normalisée).
A présent, on suppose que $x = 0,1$. Cependant, on remarque que le développement en base 2 de ce nombre est illimité périodique, ou encore $x = overline{0,00011001100110011…}^2$.
On code désormais sur 16 bits, et on donne la répartition suivante : l’exposant sur 6 bits pour coder des entiers de -31 à 32 et la mantisse sur 9 bits.
Pour pouvoir coder ce nombre, on commence par le transformer en écriture normalisée : $x = overline{1,1001100110011…}^2 times 2^{-4}$. Le codage de l’exposant se fait de la même manière que dans l’exemple précédent avec la méthode de complémentation à 2 et on trouve que $-4 = overline{111100}^2$.
Il reste à présent à coder la mantisse. Cependant, comme le développement est illimité, il faut nécessairement effectuer un arrondi car on ne peut garder qu’un nombre fini de bits (9 ici). On conserve alors 9 chiffres après la virgule et $x$ vaut alors : $x approx overline{1,100110011}^2 times 2^{-4}$.
Le codage de ce nombre est alors 0 111100 100110011. On a donc du procédé à un arrondi du nombre pour pouvoir le coder. Cet exemple a donc permis de soulever une des limites du codage en flottant, que nous allons maintenant développer.
Le calcul avec les flottants est un calcul approché. Cela s’explique tout d’abord par l’écart minimal : si deux nombres ont un écart en deçà de cet écart, alors ils sont considérés comme égaux. Une autre explication de calcul approché est l’obligation d’avoir recours à des arrondis car les écritures décimales des nombres en base 2 peuvent être illimitées et potentiellement apériodiques si le nombre n’est pas rationnel.
Si un nombre dépasse $x_{max}$ ou $x_{min}$, l’ordinateur ne peut plus les coder : c’est une erreur de dépassement de capacité, respectivement signalée par overflow et underflow.
En informatique, deux nombres sont considérés comme égaux si leur différence est inférieure à l’écart minimal $epsilon$. Ainsi $x$ et $x + dfrac{1}{2} epsilon$ sont considérés comme égaux car leur différence vaut la moitié de l’écart minimal. Dans la mesure du possible, on évitera donc d’effectuer des tests d’égalité entre flottants.
Une autre limite est le phénomène d’absorption.
On se propose d’aborder cette notion avec un exemple, en limitant la mantisse à 5 bits et en supposant qu’il n’y a pas de limite pour l’exposant pour simplifier.
On commence par calculer la somme $overline{1,10000}^2 + overline{0,000001}^2$ à la main. Le résultat est immédiat et donne $overline{1,10000}^2 + overline{0,000001}^2 = overline{1,100001}^2$.
On s’intéresse à présent à la manière dont l’ordinateur effectue ce calcul.
Il faut tout d’abord écrire les termes en écriture normalisée : $overline{1,10000}^2 + overline{0,000001}^2 = overline{1,10000}^2 times 2^0 + overline{1,00000}^2 times 2^{-6}$. On somme ensuite les deux nombres et le résultat vaut alors $overline{1,10000}^2 times 2^0$ en ne conservant que 5 chiffres pour la mantisse. On remarque alors que le résultat est différent du calcul exact, car le dernier chiffre du résultat théorique n’a pas pu être représenté : on dit alors que $overline{0,000001}^2$ a été absorbé par $ overline{1,10000}^2$.
Le phénomène de non associativité est une illustration du phénomène d’absorption.
Pour simplifier davantage, on suppose ici que la mantisse est codée sur 2 bits.
On souhaite calculer la somme $overline{1,00}^2 +overline{0,001}^2 +overline{0,001}^2 $. Le calcul direct à la main donne $overline{1,010}^2 $, en se rappelant que le calcul se fait en base 2. On a pu ici sommer le premier et le deuxième terme ensemble puis sommer le résultat avec le troisième ou bien sommer le deuxième et le troisième ensemble puis sommer le résultat avec le premier terme : c’est la propriété d’associativité de l’addition.
On s’intéresse à la manière dont va être effectué ce calcul par un ordinateur.
On effectue ce calcul de deux manières, en associant deux nombres différents à chaque fois.
$begin{aligned} overline{1,00}^2 + (overline{0,001}^2 +overline{0,001}^2) &=& overline{1,00}^2 times 2^0 + (overline{1,00}^2 times 2^{-3} +overline{1,00}^2 times 2^{-3}) \ &=& overline{1,00}^2 times 2^0 + overline{1,00}^2 times 2^{-2} \ &=& overline{1,01}^2 times 2^0 end{aligned}$
Une autre manière d’effectuer ce calcul est $(overline{1,00}^2 + overline{0,001}^2) +overline{0,001}^2 = (overline{1,00}^2 times 2^0 + overline{1,00}^2 times 2^{-3}) +overline{1,00}^2 times 2^{-3}$. En ne conservant que deux bits pour la mantisse, on constate que le phénomène d’absorption se produit pour la première somme : $(overline{1,00}^2 times 2^0 + overline{0,001}^2) +overline{0,001}^2 = overline{1,00}^2 times 2^0 + overline{1,00}^2 times 2^{-3}$. Il en est de même pour la deuxième somme.
Finalement le résultat est $(overline{1,00}^2 + overline{0,001}^2) +overline{0,001}^2 = overline{1,00}^2times 2^0 = 1$ : il n’y a donc pas associativité dans le cadre de l’addition entre flottants.
Nombres flottants 1
Nombres flottants 1
1) Notion de développement décimal d’un nombre réel
Avant de débuter la théorie sur le codage des nombres décimaux, on commence par présenter la notion de développement d’un nombre décimal à travers des exemples.
Si on considère un entier naturel, comme $x=1$, son écriture est connue et ne présente pas de difficultés.
Si on considère un nombre rationnel, comme $y = dfrac{1}{2}$, il est possible d’écrire $y$ sous une écriture décimale. En effet, $y = 0,5$. Il s’agit d’une écriture décimale finie.
Cependant, tout les nombres rationnels n’ont pas une écriture décimale finie. En effet, $z = dfrac{1}{3} = 0,3overline{3}…$. On symbolise que le développement est infini en ajoutant une barre sur le $3$ signifiant que le $3$ se répète indéfiniment. De plus, le développement décimal est périodique, c’est à dire que le motif $3$ se répète indéfiniment.
Considérons à présent le nombre $a$ dont le développement décimal est $a = 0,34overline{34}…$. Il s’agit donc d’un nombre dont le développement décimal est une répétition du motif $34$ indéfiniment. En multipliant $a$ par $100$ on obtient alors le nombre $100a = 34,overline{34}$. Il apparait alors qu’en soustrayant à ce nouveau nombre le nombre $a$, la partie décimale disparait: $100a – a = 34,overline{34} – 0,overline{34} = 34$. Or, $100a – a = 99a$.
Finalement, on a donc $99a = 34$ c’est à dire $a = dfrac{34}{99}$.
On peut montrer que l’ensemble des nombres possédant un développement décimal fini ou infinie périodique est exactement l’ensemble des nombres rationnels.
Enfin, il existe des nombres possédant un développement décimal infini non périodique (ou apériodique). Ceux sont les nombres irrationnels comme par exemple $pi =3,14…$ ou $sqrt{2} = 1,41421…$
Nous admettrons après avoir considéré l’ensemble de ces exemples que tout nombre réel $x$ peut s’écrire sous la forme :
$x = a_2a_1a_0, b_1b_2b_3…b_n… = a_2 10^2 + a_1 10^1+a_010^0 + b_1 10^{-1} + b_2 10^{-2} + b_3 10^{-3}+…+b_n10^{-n}+…$, avec $a_i in {0, 1, 2, …, 8, 9 }$, $b_i in {0, 1, 2, …, 8, 9 }$.
Il existe un nombre fini de $a_i$ mais un nombre infini de $b_i$. Si $x$ admet un développement décimal fini, les $b_i$ sont nuls à partir d’un certain rang.
Il est bon de noter toutefois que cette écriture n’est pas unique. En effet, si on s’intéresse au nombre $x = 0,overline{9}$, alors en regardant le nombre $10x – x = 9,overline{9} – 0,overline{9} = 9$, on trouve que $9x = 9$ soit $x = 1$. On retiendra alors que les développements décimaux composés d’une infinité de 9 à partir d’un certain rang sont appelés développements décimaux impropres.
Exemple :
Soit $x = 1234,56780…$,
$1234$ est la partie entière de $x$.
Il est possible d’écrire $x$ un introduisant une puissance de $10$ :
$x = 1234,56780 times 1 = 1234,56780 times 10^0$.
On peut également décaler la virgule, qui devient alors flottante (on pourra alors faire un parallèle avec l’appellation nombre flottant) :
$x = 1,2345678 times 10^3$ ou encore $x = 0,0012345678 times 10^6$.
Le nombre $x$ écrit à l’aide d’une puissance de $10$ possède donc plusieurs écritures.
Chaque écriture est composée d’une mantisse (exemple : $0,0012345678$) et d’un exposant (exemple : $6$). On remarque que chaque écriture possède un couple mantisse-exposant différent : le couple mantisse-exposant n’est pas unique.
En informatique, la règle d’écriture des nombres est d’utiliser une mantisse ne comportant qu’un nombre à gauche de la virgule, non nul.
Exemple :
$23,21 = 2,321 times 10^1$
$0,134 = 1,34 times 10^{-1}$
2) Base deux
On admet la propriété suivante :
Tout nombre réel $x$ s’écrit sous la forme :
$x = a_3a_2a_1a_0, b_1b_2b_3…b_n… $ avec $a_i in {0, 1}$; $b_i in {0, 1}$. Il existe un nombre fini de $a_i$ mais un nombre infini de $b_i$. Si $x$ admet un développement décimal fini, les $b_i$ sont nuls à partir d’un certain rang.
On peut aussi faire apparaitre les puissances de $2$ successives :
$x = a_32^3 + a_22^2 + a_12^1 +a_02^0 + b_12^{-1} + b_22^{-2}+…+b_n2^{-n}+…$.
Exemple :
Soit $x = 3,625$,
On cherche l’écriture en base $2$ de $x$.
Il s’agit pour cela de connaitre les puissances de $2$.
On remarque que $3 = 1 + 2$.
On s’intéresse à présent à la partie décimale :
$0,625 = 0,5 + 0,125$.
Or, $0,5 = dfrac{1}{2} = 2^{-1}$ et $0,125 = dfrac{1}{8} = dfrac{1}{2^3} = 2^{-3}$.
Ainsi, $x = 2 + 1 + 0,5 + 0,125 = 1times 2^1 + 1 times 2^0 + 1 times 2^{-1} + 0 times 2^{-2} + 1 times 2^{-3}$.
C’est à dire $x = overline{11,101}^2$.
En adoptant le choix standard pour l’écriture à l’aide d’une mantisse on a : $x = overline{1,1101}^2times 2^1$
Propriété :
Tout réel est représenté par son signe ($+$ ou $-$), codé par un bit de signe que l’on place sur le bit de poids fort, la mantisse $m$ et l’exposant $e$, écrits en base $2$. Le couple $(m, e)$ est normalisé, en considérant l’écriture qui fait apparaitre un seul chiffre non nul à gauche de la virgule.
Or, comme les calculs en informatiques sont effectués en base $2$, il n’y a que deux chiffres possibles $0$ ou $1$. Si le premier chiffre de la mantisse est non nul, il vaut forcément $1$. Il n’est donc pas nécessaire de coder le premier chiffre dont on connait toujours la valeur : 1.
On remarquera qu’un réel peut avoir un développement décimal illimité. En informatique, un développement décimal illimité n’a pas de sens : on procède donc à une première approximation afin d’écrire ce réel à l’aide d’un développement décimal fini.
On considère que l’exposant varie entre deux bornes $L$ (low), négatif, et $U$ (up) telles que :
$L leq e leq U$
On désigne par $t$ le nombre de chiffres de la mantisse.
Finalement, un nombre réel est codé :
– à l’aide d’un bit de signe (le bit de poids fort)
– d’un exposant
– et d’une mantisse contenant $t$ chiffres.
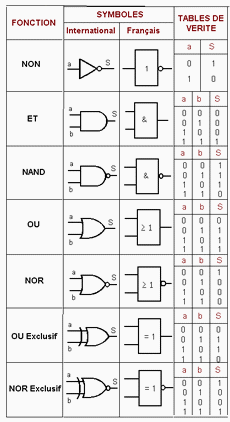
Calculs Booléens
Booléens
Un booléen est une variable informatique à deux états logiques : Vrai ou Faux, ou bien 1 ou 0. Le calcul booléen fut inventé par George Boole en XIXe siècle.
Exemple :
La proposition $1 > 2$ est une proposition fausse.
La proposition $1 neq 2$ est une proposition vraie.
D’une manière générale en informatique, les opérateurs de comparaison retournent une valeur booléenne. Les variables booléennes permettent de formaliser les raisonnements logiques pratiqués en informatique.
Les opérateurs logiques
Soient $x$ et $y$ deux propositions,
Il est possible de définir différents opérateurs logiques :
– la négation de $x$, noté $overline{x}$, que l’on appelle not $x$. Cette proposition prend la valeur logique opposée à celle de $x$
Exemple :
Lorsque $x$ est fausse, $overline{x}$ est vraie.
Lorsque $x$ est vraie, $overline{x}$ est fausse.
– la conjonction de $x$ et $y$, notée $x$ ET $y$ ou $x.y$. Cette proposition est vraie uniquement lorsque $x$ et $y$ sont simultanément vraies.
Exemple :
Si $x$ est fausse et $y$ est vraie, alors $x.y$ est fausse.
– la disjonction de $x$ et $y$ que l’on note $x$ OU $y$, $x + y$. Il est aussi possible de définir cet opérateur à l’aide de la négation et de la conjonction $overline{overline{x}.overline{y}}$.
Exemples :
Considérons que $x$ et $y$ sont fausses, alors $overline{x}$ et $overline{y}$ sont vraies, donc $overline{x}.overline{y}$ est vraie. Or la négation d’une proposition vraie est une proposition fausse, donc $overline{overline{x}.overline{y}}$ est fausse. Ainsi, $x+y$ est fausse.
Considérons que $x$ est vraie et que $y$ est fausse, alors $overline{x}$ est fausse et $overline{y}$ est vraie, donc $overline{x}.overline{y}$ est fausse. Or la négation d’une proposition fausse est une proposition vraie, donc $overline{overline{x}.overline{y}}$ est vraie. Ainsi, $x+y$ est vraie.
On fera cependant attention que $+$ n’a pas toujours le sens d’une addition au sens mathématique du terme.
En effet, si $x$ et $y$ sont vraies et valent donc $1$, alors $x+y$ est vraie aussi et vaut $1$.
De plus, on peut remarquer que le OU n’a pas toujours le même sens qu’en français. Il s’agit en effet d’un OU inclusif : quand $x$ et $y$ sont toutes deux vraies, $x$ OU $y$ est vraie.
On retiendra que la disjonction n’est fausse uniquement lorsque $x$ et $y$ sont fausses.
– l’implication, que l’on note $x Rightarrow y$, qui correspond par définition à la proposition $overline{x}+y$.
Exemple :
Supposons que $x$ et $y$ sont fausses, alors $overline{x}$ est vraie donc $overline{x}+y$ est vraie. Ainsi, $x Rightarrow y$ est vraie.
On remarque que dès lors que l’hypothèse initiale est fausse, l’assertion totale est juste. On retiendra que l’implication est toujours vraie sauf lorsque $x$ est vraie et $y$ fausse.
– la disjonction exclusive de $x$ et $y$, que l’on note $x oplus y$, qui correspond au OU exclusif en français : les deux propositions ne peuvent pas être vraies en même temps.
Exemple :
Supposons $x$ vraie et $y$ fausse, alors $xoplus y$ est vraie.
Supposons $x$ et $y$ vraies, alors $xoplus y$ est fausse.
On regroupe l’ensemble des résultats précédents dans la table de vérité suivante
| $x$ | $y$ | $overline{x}$ | $x.y$ | $x+y$ | $x Rightarrow y$ | $xoplus y$ |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 |
Exemple :
On se propose ici d’appliquer à un exemple concret les différents opérateurs décrits précédemment.
Soient $x$ la proposition “je suis sec” et $y$ la proposition “je suis mouillé”,
On peut remarquer que si je ne suis pas sec, alors je suis mouillé, ce qui signifie que $y$ est la négation de $x$ et réciproquement, ce que l’on écrit en mathématiques $overline{x} = y$ et $overline{y} = x$.
La proposition “je suis sec OU je suis mouillé” est vraie car toute personne est forcément dans l’un des deux états, ainsi $x+y =1$.
La proposition “je suis sec ET je suis mouillé” est fausse car toute personne ne peut pas être dans le même état simultanément, ainsi $x.y =0$.
Plus généralement, on peut remarquer que :
– la proposition $x$ ou $overline{x}$ est fausse, c’est à dire $x.overline{x} = 0$ : c’est ce qu’on appelle le principe de non-contradiction.
– la proposition $x$ et $overline{x}$ est vraie, c’est à dire $x + overline{x} = 1$ : c’est ce qu’on appelle le principe du tiers exclu.
– la négation de la négation prend les mêmes valeurs logiques que la proposition initiale.
– l’implication $x Rightarrow y$ prend les mêmes valeurs logiques que l’implication $overline{y} Rightarrow overline{x}$ : c’est la contraposée.
En effet, supposons par exemple que l’assertion “s’il pleut alors j’ai mon parapluie” est vraie. Alors, “si je n’ai pas mon parapluie alors il ne pleut pas” est vraie car si il avait plu j’aurai eu mon parapluie.
– la négation de la disjonction de $x$ ou $y$ prend les mêmes valeurs logiques que la conjonction de $overline{x}$ et $overline{y}$. On note donc : $overline{x+y} = overline{x} . overline{y}$.
– de même, la négation de la conjonction de $x$ et $y$ prend les mêmes valeurs logiques que la disjonction de $overline{x}$ ou $overline{y}$. On note donc : $overline{x.y} = overline{x} + overline{y}$.
Enfin, on s’intéresse à la négation de l’implication $x Rightarrow y$, qui vaut par définition $overline{overline{x}+y}$. D’après une propriété précédente, $overline{overline{x}+y} = overline{overline{x}}.overline{y}$. Enfin, $overline{overline{x}} = x$ donc $overline{overline{x}}.overline{y} = x.overline{y}$
Les fonctions booléennes peuvent être réalisées par des circuits électroniques.