Taux global & taux réciproque
Taux global & taux réciproque
Taux global, évolutions successives
Un nombre $V_0$ peut évoluer, il peut subir des augmentations ou des diminutions successives jusqu’à une valeur finale $V_n$ que l’on souhaite déterminer.
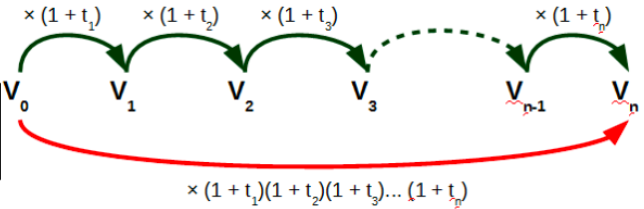
Pour ce faire, il s’agit de multiplier la valeur initiale par le coefficient multiplicateur global, défini par :
$ 1 +t_g = (1 + t_1) \times (1 + t_2) \times (1+t_3) \times …\times (1+t_n)$
où $( 1 + t_1)$ est le coefficient multiplicateur de la première évolution, $(1 + t_2)$ le coefficient multiplicateur de la seconde évolution, etc.
Ainsi pour obtenir le coefficient multiplicateur global, il faut multiplier les coefficients multiplicateurs des évolutions entre-eux.
Par exemple, un salaire de 2547,5 € baisse de 3% puis augmente de 12%, il en résulte alors qu’il vaut
$S = 2547,5 \times \left ( 1 – \dfrac{3}{100} \right ) \times \left ( 1 + \dfrac{12}{100} \right ) $
$S= 2547,5 \times 0,97 \times 1,12 = 2767,6$ €.
On remarquera qu’il ne faut pas additionner les pourcentages des évolutions pour trouver le résultat final.
Taux réciproque
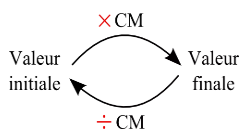
Si un nombre évolue d’une valeur initiale à une valeur finale avec un coefficient multiplicateur $CM= (1 + t)$, alors pour revenir à la valeur initiale, il faut multiplier la valeur finale par $\dfrac{1}{1 + t}$, (ce qui revient à diviser par $CM$)
En d’autres termes, le nouveau coefficient multiplicateur est défini par $ 1 + t’ = \dfrac{1}{1 + t}$.
Par exemple, une maison subit une hausse de 15%. Calculons le pourcentage de la baisse pour revenir au prix initial :
$1 + t’ = \dfrac{1}{1 + 0,15}$, c’est à dire $t’ = \dfrac{1}{1 + 0,15} – 1 \approx -0,1304$, soit une baisse de 13% environ.
Pourcentages, taux d'évolutions
Pourcentages, taux d’évolutions
Calculer un pourcentage
Afin de calculer un pourcentage, il s’agit de faire le rapport de la partie étudiée par l’ensemble puis de multiplier le résultat par 100.
Par exemple, si l’on s’intéresse au pourcentage de filles dans une classe de 30 élèves où 18 sont des filles, il y a alors $p = \dfrac{18}{30} \times 100 = 60 \%$ de filles.
Taux d’évolution
Le taux d’évolution permet de caractériser l’évolution d’un nombre entre sa valeur initiale $V_i$ et sa valeur finale $V_f$. Il est défini par $t = \dfrac{V_f – V_i}{V_i}$
Par exemple, la population d’une ville est passée de 145 à 167 habitants, soit une évolution de $t = \dfrac{167 – 145}{145} \approx 0,1517 \approx 15,17 \%$.
Coefficient multiplicateur
Augmenter de $t \% $ revient à multiplier par $\left ( 1 + \dfrac{t}{100} \right )$, c’est le coefficient multiplicateur.
Si par exemple un salaire de $2540€$ augmente de $5 \%$, le nouveau salaire est à présent de $S = \left ( 1 + \dfrac{5}{100} \right ) \times 2540 = 1,05 \times 2540 = 2667 $ €.
Diminuer de $t \% $ revient à multiplier par $\left ( 1 – \dfrac{t}{100} \right )$.
Taux moyen
Taux moyen
Un nombre peut subir diverses évolutions, il peut augmenter ou baisser en $n$ évolutions. La valeur initiale du nombre a dont été multipliée par des coefficients multiplicateurs différents au nombre de $n$.
Le taux moyen correspond au taux qui multiplié $n$ fois par lui même donne la même évolution finale et est donné par la formule :
$(1 + t_m)^n = 1 + t_g$,
Le taux moyen répété $n$ fois donne le taux global.
Considérons par exemple un objet qui vaut 273€ en 2001 puis 430€ en 2005, le taux global est égal à
$t_g = \dfrac{\text{valeur finale} – \text{valeur initiale}}{\text{valeur initiale}} = \dfrac{430 – 273}{273} \approx 0,5751$.
Par définition du taux moyen, pour une évolution sur 4 ans, vaut
$(1 + t_m)^4 = 1 + t_g \approx 1,5751$.
Ainsi, $1 + t_m \approx 1,5751^{1/4}$ soit
$t_m \approx 1,5751^{1/4} – 1 \approx 0,1203 \approx 12,03 \% $