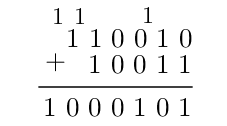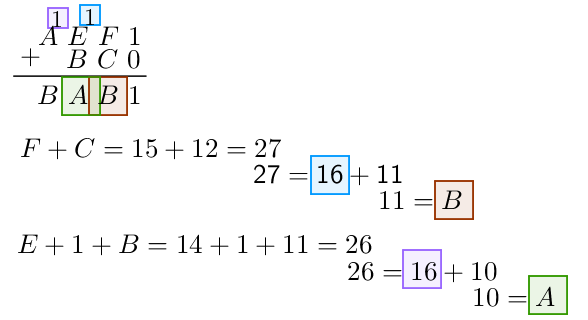Nombres entiers en base deux, dix, seize
I. Notions de base
La base naturelle que nous utilisons quotidiennement est la base 10. En informatique, les bases 2 (base binaire) et 16 (base hexadécimale) sont utilisées.
On illustre à travers des exemples les notions de base.
On commence par la base 10.
On écrit alors le nombre $357$ et on se demande à quoi il est égal. On le décompose alors en utilisant des puissances de $10$ successives.
$357 = 7 times 10^0 + 5 times 10^1 + 3 times 10^2$
Pour écrire tous les nombres entiers en base 10, on utilise 10 chiffres qui sont 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
La base 2 fait intervenir deux chiffres : 0 et 1.
On se demande à quel nombre correspond l’écriture en base 2 suivante : $overline{10111}^2$.
On décompose alors ce nombre en faisant intervenir des puissances de 2 successives.
$begin{aligned} overline{10111}^2 &=& 1times 2^0 + 1 times 2^1 + 1 times 2^2 + 0 times 2^3 + 1 times 2^4 \ &=& 1 + 2 + 4 + 16 \ &=& 23 end{aligned}$
La base 16 nécessite l’utilisation de 16 chiffres. On utilise alors les 10 chiffres usuels auxquels on rajoute les 6 premières lettres de l’alphabet.
Les symboles utilisés sont donc 0, 1, 2, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Ainsi, la lettre A correspond au nombre 10, B au nombre 11, …
On se demande donc à quel nombre correspond l’écriture en base 16 suivante : $overline{B2E}^{16}$.
On décompose alors ce nombre en faisant intervenir des puissances de 16 successives.
$begin{aligned} overline{B2E}^{16} &=& 14 times 16^0 + 2 times 16^1 + 11 times 16^2 \ &=& 14 + 32 + 2816 \ &=& 2862 end{aligned}$
II. Passage entre bases
1. On s’intéresse au passage d’un nombre écrit en base 10 à une écriture en base 2 ou 16
Pour obtenir cette nouvelle écriture, on procède par divisions euclidiennes successives par la base choisie et on s’arrête lorsque le quotient devient nul.
En remontant la colonne des restes, on obtient l’écriture dans la base choisie du nombre de départ.
Exemples :
On souhaite écrire $73$ en base 2.
On procède donc par divisions euclidiennes successives.
| Dividende | Diviseur | Quotient | Reste |
| 73 | 2 | 36 | 1 |
| 36 | 2 | 18 | 0 |
| 18 | 2 | 9 | 0 |
| 9 | 2 | 4 | 1 |
| 4 | 2 | 2 | 0 |
| 2 | 2 | 1 | 0 |
| 1 | 2 | 0 | 1 |
Ainsi, $73 = overline{1001001}^2$
On souhaite de même trouver l’écriture en base 16 de 3741.
| Dividende | Diviseur | Quotient | Reste |
| 3741 | 16 | 233 | 13 |
| 233 | 16 | 14 | 9 |
| 14 | 16 | 0 | 14 |
Pour conclure, on doit trouver la lettre correspondante aux nombres 13 et 14, qui est respectivement D et E.
Ainsi, en remontant la colonne des restes on trouve :
$3741 = overline{E9D}^{16}$
2. On s’intéresse au passage d’un nombre écrit en base 2 ou 16 à une écriture en base 2 ou 16
Pour obtenir cette conversion, on peut remarquer que $16 = 2^4$.
Pour se faire, on décompose chaque chiffre de la base hexadécimale en base 2.
| 0 : 0000 | 4 : 0100 | 8 : 1000 | C : 1100 |
| 1 : 0001 | 5 : 0101 | 9 : 1001 | D : 1101 |
| 2 : 0010 | 6 : 0110 | A : 1010 | E : 1110 |
| 3 : 0011 | 7 : 0111 | B : 1011 | F : 1111 |
Exemples :
On part du nombre écrit en base hexadécimale (base 16) : $overline{6C5}^{16}$ et on décompose chaque chiffre en base 2, en veillant à utiliser quatre chiffres de la base 2 par conversion, même si cela conduit à écrire des 0 inutiles.
$6 = overline{0110}^2$
$C = overline{1100}^2$
$5 = overline{0101}^2$
Ainsi, $overline{6C5}^{16} = overline{011011000101}^2$
De même, si $n = overline{10100111010111}^2$, on regroupe les chiffres par groupe de 4 en partant du chiffre des unités (de la droite) et on utilise le tableau de conversion.
| 10 | 1001 | 1101 | 0111 |
| 2 | 9 | D | 7 |
Finalement, $n = overline{29D7}^{16}$.
III. Opérations
On s’intéresse désormais à l’addition de deux nombres écrits en base 2 ou en base 16.
Lorsque les nombres sont écrits en base 2, si l’on effectue l’addition $1 + 1$ le résultat vaut 0 en l’on retient 1.
Lorsque les nombres sont écrits en base 2, si la somme est supérieure à 15, on inscrit dans la colonne le résultat de la différence de ce nombre et de 16, que l’on convertit éventuellement en base 16, et on retient 1 pour la colonne suivante.
Exemples :
1) On considère $n = overline{10011}^2$ et $p = overline{110010}^2$.
On regarde la somme $n + p$.
Finalement $n + p = overline{100101}^2$
On peut alors vérifier en écrivant chaque nombre en base 10.
$n = 16 + 2 + 1 = 19$
$p = 32 + 16 + 2 = 50$
$n + p = 64 + 4 + 1 = 69$
2) On considère $n = overline{AEF1}^{16} = 44785$ et $p = overline{BC0}^{16} = 3008$.
On peut alors vérifier en écrivant les nombres en base 10 :
$n + p = 47793$