Intensité d'un courant électrique
I. Introduction
Au commencement : l’électron
L’électron a une masse $m_e = 9,31 \times 10^{-31} kg$ et une charge négative $q_e = -1,6\times 10^{-19} C.$
C’est l’un des constituants de l’atome avec protons et neutrons, qui sont eux les constituants du noyau autour duquel gravitent les électrons. Les électrons forment un nuage électronique dans l’atome.
Qu’est-ce qu’un conducteur ?
Un conducteur est un cas particulier où les atomes appelés cations sont fixes sur un réseau et vont perdre un électron. Chaque atome va libérer un électron, qui va être libre et donc mobile. Tant que la matière n’est soumise à aucune tension, chaque électron va se déplacer de manière aléatoire de la même façon que dans un gaz. La vitesse moyenne de tous les électrons ensemble est une vitesse qui est nulle.
II. L’intensité du courant électrique
Le courant électrique
Quand on va commencer à mettre une tension sur le métal, les électrons vont avoir tendance à se déplacer tous à la même vitesse. Il reste un côté aléatoire mais ils ont globalement tous tendance à s’orienter dans la même direction. La vitesse moyenne des électrons à ce moment-là ne sera plus nulle. Le courant électrique est donc le déplacement moyen de l’ensemble des électrons dans une unique direction.
Relation entre $I$ et $Δq$
On définit une surface virtuelle où l’on va couper l’échantillon de matière et compter le nombre d’électrons qui passe à travers cette surface. Si le comptage des électrons a duré cinq secondes par exemple, l’intensité électrique sera donc caractérisée par le nombre de charges multiplié par la charge de l’électron divisé par le temps qu’on a mis pour compter ces charges.
L’intensité électrique est donc la quantité de charges comptée durant une certaine durée Δt :
$I = \dfrac{Δq}{ Δt}$
Avec $I$ en $A, Δq$ en $C$ et $Δt$ en $s.$
Source réelle de tension continue
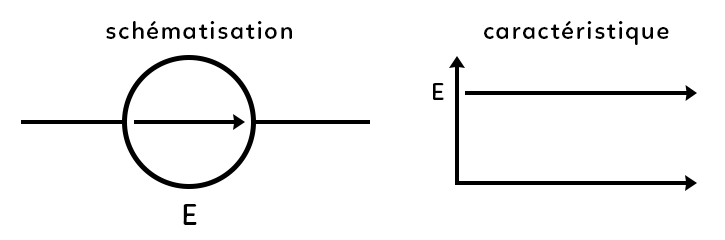
I. Rappel : source de tension idéale
La flèche indique le sens de la tension et E caractérise la tension délivrée par la source de tension idéale. La caractéristique de cette source de tension idéale est que la tension est égale à E quelle que soit l’intensité électrique. La tension ne dépend donc pas de l’intensité électrique et délivre toujours la même tension quelle que soit l’intensité électrique.
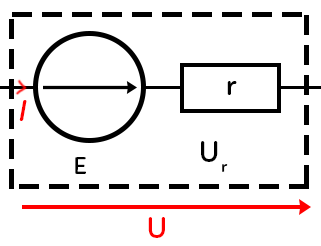
II. Source réelle de tension continue
Dans une source réelle de tension continue, on met en série une source idéale avec une résistance : l’ensemble constitue la source réelle. On se place en convention générateur puisque l’on a un générateur : ici l’intensité et la tension électrique sont dans le même sens.
On cherche la loi $U = f(I),$ c’est-à-dire que l’on recherche à caractériser la tension $U$ en fonction de l’intensité $I$ cette fois-ci pour une source réelle.
Si l’on applique tout d’abord la loi des mailles, on a $U = E – U_r $car $E$ et $U_r$ sont de sens opposés.
La loi d’Ohm dit que : $U_r = r \times I$
On peut donc écrire que : $U = E – r \times I$ (relation générale pour une source réelle de tension)
On peut tracer un graphique avec cette fonction avec $E$ l’ordonnée à l’origine et $r$ le coefficient directeur. On a une relation affine entre $U$ et $I.$
$E$ : tension à vide (en Volt V), c’est-à-dire la tension quand il n’y a aucune intensité débitée.
$r$ : résistance interne (en Ohm $Ω$)
III. Conséquences pratiques
Comme il y a une résistance à l’intérieur du générateur, celui-ci va s’échauffer par effet Joule.
Il va y avoir une chute de tension quand la source va débiter du courant.
Exemple
Un pile qui délivre une tension à vide $E = 1,5 V$ et qui a une résistance interne $r = 2Ω.$
On l’utilise avec un courant de sortie $I = 100 mA = 0,1 A.$
Donc $U = 1,5 – 2 \times 0,1 = 1,3 V$