Le Soleil : perte de masse et profil spectral
Le Soleil : perte de masse et profil spectral
I. Perte de masse du Soleil
Le Soleil fait des réactions de fusion nucléaire en son cœur, ce qui transforme une partie de sa masse en énergie. Ainsi, au cours de ces réactions de fusion, de l’énergie est libérée. Une question se pose alors : quelle est la perte de masse (transformée en énergie) du Soleil en une seconde ?
Certaines données sont utiles pour répondre à cette question :
– la puissance rayonnée par le Soleil : $P_{rayonnée} = 3.9 times 10^{26} W$,
– la relation entre l’énergie et la puissance : $E (J)=P (W) times delta t (s)$,
– la relation d’Einstein : $E (J)=delta m (kg) times c^2 (m/s)$.
En fusionnant les deux dernières relations on obtient :
$delta m times c^2 = P times delta t $, d’où $delta m = dfrac{P times delta t}{c^2}=dfrac{P }{c^2}$ pour 1 seconde.
L’application numérique donne $delta m = dfrac{3.9 times 10^{26}}{(3.0 times 10^8)^2}=4.3 times 10^9 kg$.
II. Profil spectral
Le profil spectral du Soleil est la fonction énergie dépendant de la longueur d’onde.
La courbe du profil spectral possède toujours un maximum. Ce maximum est graphiquement relié à la longueur d’onde pour laquelle l’énergie est maximale, on note cette longueur d’onde $lambda_{max}$.
Ce profil spectral correspond à un corps noir, par exemple un astre. On peut, à partir de la Loi de Wien, déterminer la température du corps noir. Cette loi est : $T(K)=dfrac{cste}{lambda_{max}}$.
Variation de l'énergie reçue à la surface de la Terre
Variation de l’énergie reçue à la surface de la Terre
Du fait que la Terre est ronde, tourne sur elle-même et tourne autour du Soleil (en environ un an), selon l’endroit où l’on se trouve sur Terre on ne va pas recevoir la même quantité d’énergie selon le moment de l’année. Il y des variations de la quantité d’énergie que reçoit un point donné à la surface de la Terre. On perçoit cette énergie sous forme de lumière et de chaleur.
I. Variations diurnes
Les variations diurnes est l’alternance jour/nuit. La Terre tourne sur elle-même, et donc pour un point donné (par exemple la France), on n’est pas toujours face au Soleil. Selon le moment de la journée, la France va se retrouver sur la face exposée au Soleil ou au contraire sur la face qui n’est pas exposée au Soleil. Si elle est face au Soleil, il fait jour et l’énergie reçue est plus importante que quand il fait nuit est que la France est sur la face non exposée au Soleil.
II. Variations selon la latitude
La latitude est la distance par rapport à l’Équateur. Une latitude s’exprime en degrés :
– Lorsqu’on est à l’Équateur on dit que la latitude est nulle.
– Lorsqu’on est aux Pôles (Nord ou Sud), la latitude est de 90°.
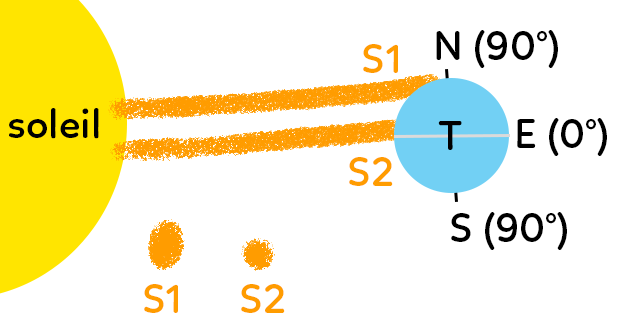
L’énergie est reçue différemment selon que l’on se trouve aux faibles ou fortes latitudes. Cette variation est due au fait que la Terre est ronde, et que du fait de cette forme (on parle de rotondité de la Terre), les rayons qui parviennent du Soleil ne percutent pas la surface de la Terre de la même façon.
Si on représente de façon très simplifiée la Terre, le Soleil et deux rayons symbolisant une même quantité d’énergie envoyée par le Soleil (qui sont de même épaisseur, et représentent une certaine quantité d’énergie) qui viennent frapper la surface de la Terre, on observe que :
– le rayon frappant la Terre sur des latitudes élevées (proches des Pôles), s’étale sur une surface S1 relativement grande,
– le rayon frappant la Terre sur de basses latitudes (au niveau de l’Équateur), s’étale sur une surface S2 inférieure à S1.
Comme les deux surfaces S1 et S2 reçoivent au final la même quantité d’énergie, chaque point de S1 on recevra moins d’énergie que chaque point de S2. Le total d’énergie reçue est le même, mais la quantité d’énergie reçue en un point donné de chacune de ces zones est inférieure en S1 par rapport à S2.
On dit également qu’à 60°, que l’on soit au Nord ou au Sud, la quantité d’énergie reçue par unité de surface et deux fois plus réduite qu’à l’Équateur. Donc la rotondité de la Terre est la source de la variation de la quantité d’énergie reçue en un point de la Terre.
III. Variations saisonnières
En un point donné selon la saison, la quantité d’énergie varie également. En effet, par exemple en France, il ne fait globalement pas la même température en hiver et en été.
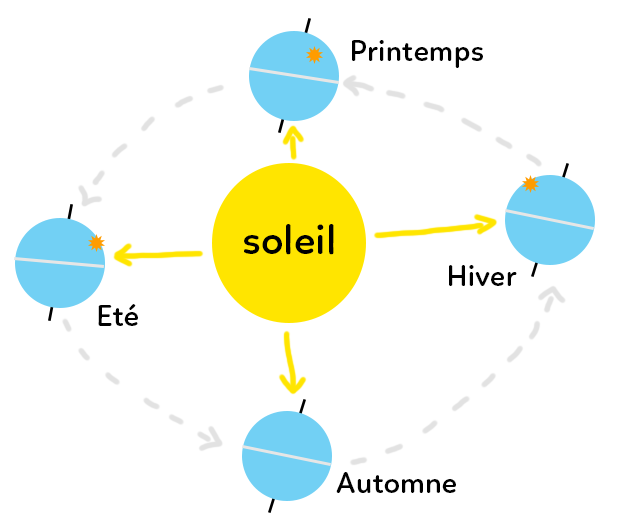
Si on représente la rotation de la Terre autour du Soleil (échelles non respectées), on peut voir que la Terre décrit une ellipse autour du Soleil (une sorte d’ovale). Il faut également prendre en compte le fait que la Terre n’est pas droite : l’axe de rotation de la Terre sur elle-même n’est pas perpendiculaire au plan de l’ellipse qu’elle décrit autour du Soleil. Plus précisément l’axe de rotation de la Terre sur elle-même forme un angle d’environ 23° avec la perpendiculaire au plan de l’écliptique (en jaune), c’est-à-dire au plan de la trajectoire de la Terre autour du Soleil. On dit que la Terre est inclinée par rapport à la normale, ou par rapport à la perpendiculaire au plan de l’écliptique.
Un même point de la Terre (par exemple la France) ne reçoit pas la même quantité d’énergie selon la saison. En été, la quantité d’énergie reçue en France est maximale, alors qu’en hiver elle est minimale. Au printemps et à l’automne, les quantités d’énergie reçue sont intermédiaires.
Cette variation est donc due :
– au fait que l’axe n’est pas perpendiculaire à l’écliptique ;
– au fait que la Terre est ronde. La position de la France va tantôt se retrouver dans une position qui ressemble au point S2 évoqué plus tôt, et tantôt au point S1. Quand la France est plutôt vers le point S1, on y reçoit moins d’énergie par unité de surface. Quand elle est dans une situation plutôt équivalente à S2 on y reçoit plus d’énergie par unité de surface : c’est l’été.